Gaussian Process Upper Confidence Bounds in Distributed Point Target Tracking over Wireless Sensor Networks

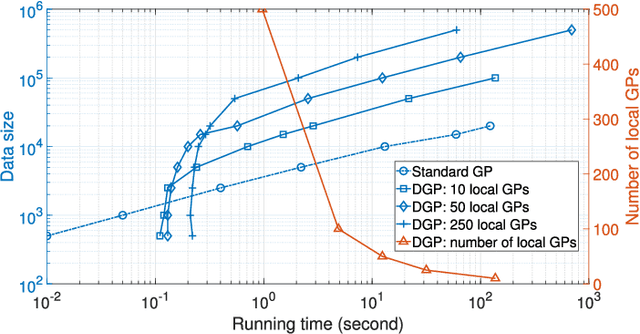
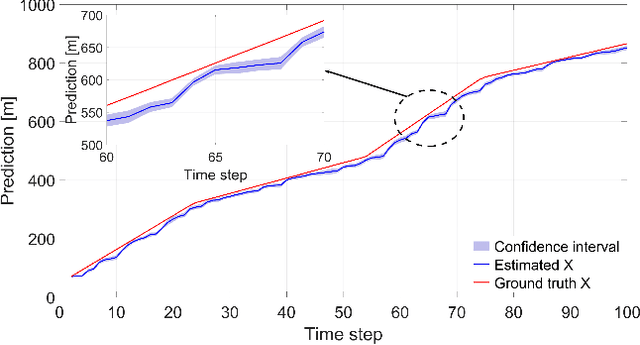
Uncertainty quantification plays a key role in the development of autonomous systems, decision-making, and tracking over wireless sensor networks (WSNs). However, there is a need of providing uncertainty confidence bounds, especially for distributed machine learning-based tracking, dealing with different volumes of data collected by sensors. This paper aims to fill in this gap and proposes a distributed Gaussian process (DGP) approach for point target tracking and derives upper confidence bounds (UCBs) of the state estimates. A unique contribution of this paper includes the derived theoretical guarantees on the proposed approach and its maximum accuracy for tracking with and without clutter measurements. Particularly, the developed approaches with uncertainty bounds are generic and can provide trustworthy solutions with an increased level of reliability. A novel hybrid Bayesian filtering method is proposed to enhance the DGP approach by adopting a Poisson measurement likelihood model. The proposed approaches are validated over a WSN case study, where sensors have limited sensing ranges. Numerical results demonstrate the tracking accuracy and robustness of the proposed approaches. The derived UCBs constitute a tool for trustworthiness evaluation of DGP approaches. The simulation results reveal that the proposed UCBs successfully encompass the true target states with 88% and 42% higher probability in X and Y coordinates, respectively, when compared to the confidence interval-based method.

Asynchronous Local Computations in Distributed Bayesian Learning

Due to the expanding scope of machine learning (ML) to the fields of sensor networking, cooperative robotics and many other multi-agent systems, distributed deployment of inference algorithms has received a lot of attention. These algorithms involve collaboratively learning unknown parameters from dispersed data collected by multiple agents. There are two competing aspects in such algorithms, namely, intra-agent computation and inter-agent communication. Traditionally, algorithms are designed to perform both synchronously. However, certain circumstances need frugal use of communication channels as they are either unreliable, time-consuming, or resource-expensive. In this paper, we propose gossip-based asynchronous communication to leverage fast computations and reduce communication overhead simultaneously. We analyze the effects of multiple (local) intra-agent computations by the active agents between successive inter-agent communications. For local computations, Bayesian sampling via unadjusted Langevin algorithm (ULA) MCMC is utilized. The communication is assumed to be over a connected graph (e.g., as in decentralized learning), however, the results can be extended to coordinated communication where there is a central server (e.g., federated learning). We theoretically quantify the convergence rates in the process. To demonstrate the efficacy of the proposed algorithm, we present simulations on a toy problem as well as on real world data sets to train ML models to perform classification tasks. We observe faster initial convergence and improved performance accuracy, especially in the low data range. We achieve on average 78% and over 90% classification accuracy respectively on the Gamma Telescope and mHealth data sets from the UCI ML repository.

Reinforcement Learning with an Abrupt Model Change

The problem of reinforcement learning is considered where the environment or the model undergoes a change. An algorithm is proposed that an agent can apply in such a problem to achieve the optimal long-time discounted reward. The algorithm is model-free and learns the optimal policy by interacting with the environment. It is shown that the proposed algorithm has strong optimality properties. The effectiveness of the algorithm is also demonstrated using simulation results. The proposed algorithm exploits a fundamental reward-detection trade-off present in these problems and uses a quickest change detection algorithm to detect the model change. Recommendations are provided for faster detection of model changes and for smart initialization strategies.

Asynchronous Bayesian Learning over a Network

We present a practical asynchronous data fusion model for networked agents to perform distributed Bayesian learning without sharing raw data. Our algorithm uses a gossip-based approach where pairs of randomly selected agents employ unadjusted Langevin dynamics for parameter sampling. We also introduce an event-triggered mechanism to further reduce communication between gossiping agents. These mechanisms drastically reduce communication overhead and help avoid bottlenecks commonly experienced with distributed algorithms. In addition, the reduced link utilization by the algorithm is expected to increase resiliency to occasional link failure. We establish mathematical guarantees for our algorithm and demonstrate its effectiveness via numerical experiments.

A Scalable Graph-Theoretic Distributed Framework for Cooperative Multi-Agent Reinforcement Learning

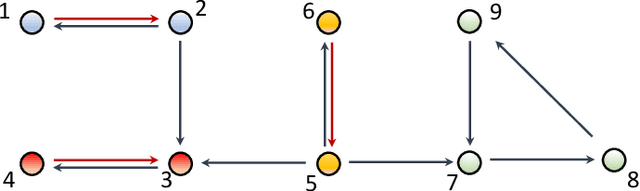
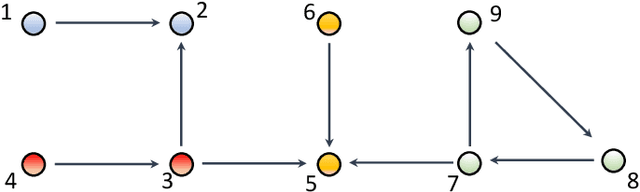
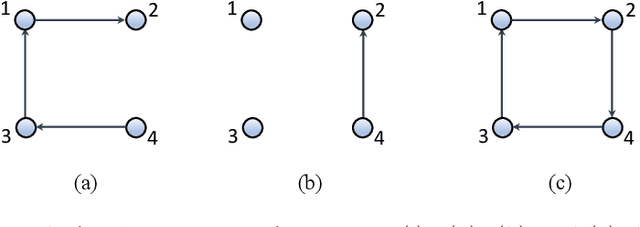
The main challenge of large-scale cooperative multi-agent reinforcement learning (MARL) is two-fold: (i) the RL algorithm is desired to be distributed due to limited resource for each individual agent; (ii) issues on convergence or computational complexity emerge due to the curse of dimensionality. Unfortunately, most of existing distributed RL references only focus on ensuring that the individual policy-seeking process of each agent is based on local information, but fail to solve the scalability issue induced by high dimensions of the state and action spaces when facing large-scale networks. In this paper, we propose a general distributed framework for cooperative MARL by utilizing the structures of graphs involved in this problem. We introduce three graphs in MARL, namely, the coordination graph, the observation graph and the reward graph. Based on these three graphs, and a given communication graph, we propose two distributed RL approaches. The first approach utilizes the inherent decomposability property of the problem itself, whose efficiency depends on the structures of the aforementioned four graphs, and is able to produce a high performance under specific graphical conditions. The second approach provides an approximate solution and is applicable for any graphs. Here the approximation error depends on an artificially designed index. The choice of this index is a trade-off between minimizing the approximation error and reducing the computational complexity. Simulations show that our RL algorithms have a significantly improved scalability to large-scale MASs compared with centralized and consensus-based distributed RL algorithms.

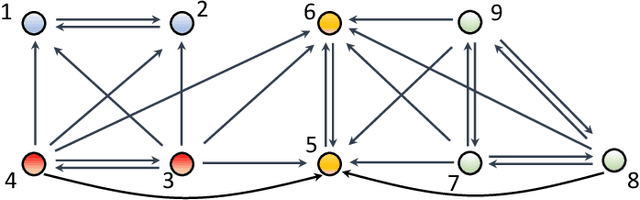
Distributed Cooperative Multi-Agent Reinforcement Learning with Directed Coordination Graph

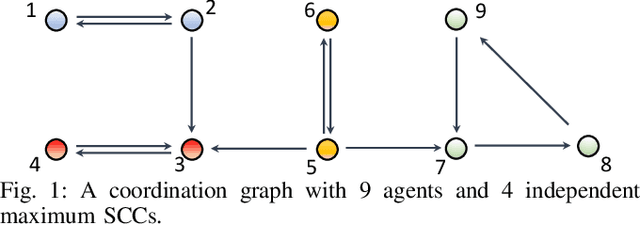
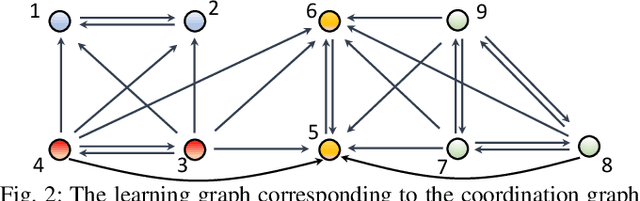
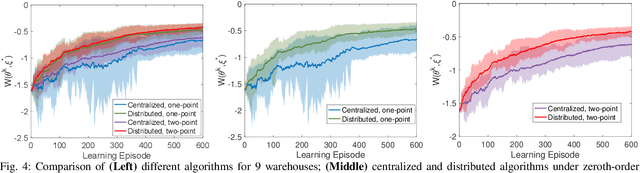
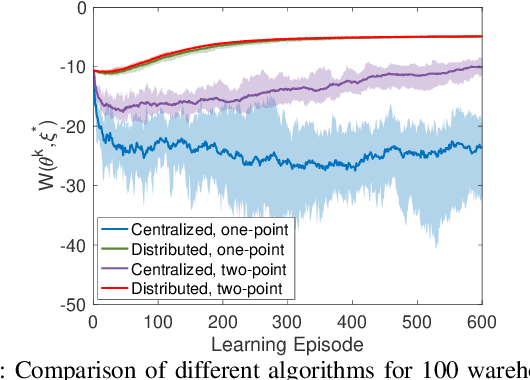
Existing distributed cooperative multi-agent reinforcement learning (MARL) frameworks usually assume undirected coordination graphs and communication graphs while estimating a global reward via consensus algorithms for policy evaluation. Such a framework may induce expensive communication costs and exhibit poor scalability due to requirement of global consensus. In this work, we study MARLs with directed coordination graphs, and propose a distributed RL algorithm where the local policy evaluations are based on local value functions. The local value function of each agent is obtained by local communication with its neighbors through a directed learning-induced communication graph, without using any consensus algorithm. A zeroth-order optimization (ZOO) approach based on parameter perturbation is employed to achieve gradient estimation. By comparing with existing ZOO-based RL algorithms, we show that our proposed distributed RL algorithm guarantees high scalability. A distributed resource allocation example is shown to illustrate the effectiveness of our algorithm.

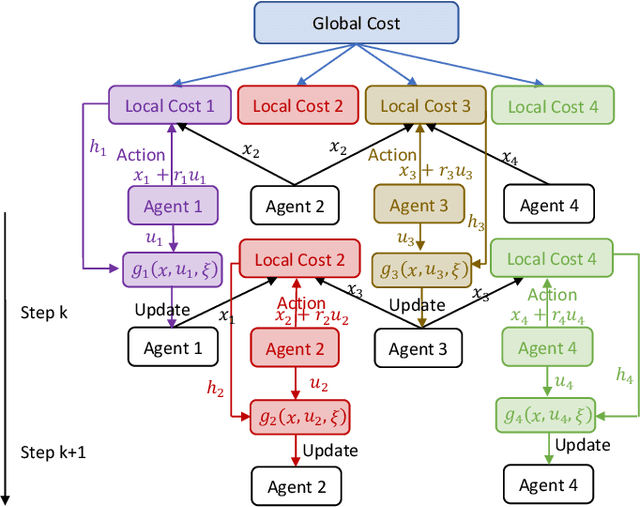
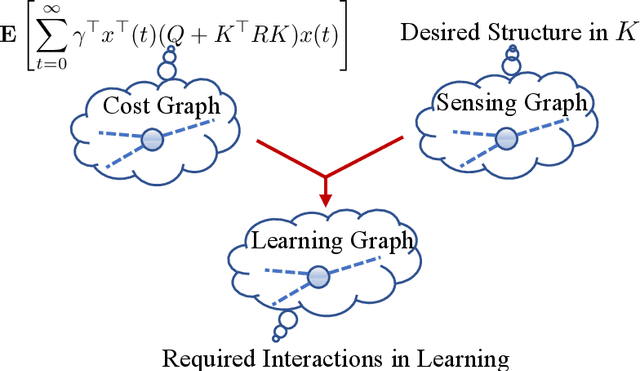
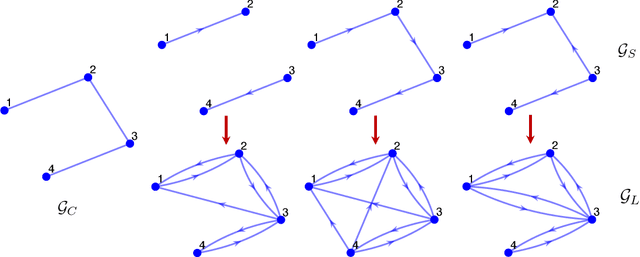
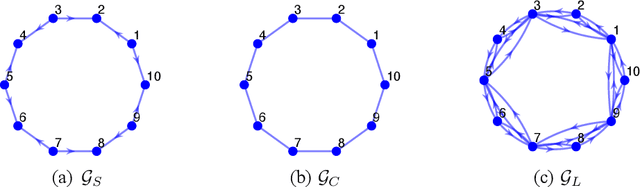
Asynchronous Distributed Reinforcement Learning for LQR Control via Zeroth-Order Block Coordinate Descent

Recently introduced distributed zeroth-order optimization (ZOO) algorithms have shown their utility in distributed reinforcement learning (RL). Unfortunately, in the gradient estimation process, almost all of them require random samples with the same dimension as the global variable and/or require evaluation of the global cost function, which may induce high estimation variance for large-scale networks. In this paper, we propose a novel distributed zeroth-order algorithm by leveraging the network structure inherent in the optimization objective, which allows each agent to estimate its local gradient by local cost evaluation independently, without use of any consensus protocol. The proposed algorithm exhibits an asynchronous update scheme, and is designed for stochastic non-convex optimization with a possibly non-convex feasible domain based on the block coordinate descent method. The algorithm is later employed as a distributed model-free RL algorithm for distributed linear quadratic regulator design, where a learning graph is designed to describe the required interaction relationship among agents in distributed learning. We provide an empirical validation of the proposed algorithm to benchmark its performance on convergence rate and variance against a centralized ZOO algorithm.

Hierarchical Reinforcement Learning for Optimal Control of Linear Multi-Agent Systems: the Homogeneous Case

Individual agents in a multi-agent system (MAS) may have decoupled open-loop dynamics, but a cooperative control objective usually results in coupled closed-loop dynamics thereby making the control design computationally expensive. The computation time becomes even higher when a learning strategy such as reinforcement learning (RL) needs to be applied to deal with the situation when the agents dynamics are not known. To resolve this problem, this paper proposes a hierarchical RL scheme for a linear quadratic regulator (LQR) design in a continuous-time linear MAS. The idea is to exploit the structural properties of two graphs embedded in the $Q$ and $R$ weighting matrices in the LQR objective to define an orthogonal transformation that can convert the original LQR design to multiple decoupled smaller-sized LQR designs. We show that if the MAS is homogeneous then this decomposition retains closed-loop optimality. Conditions for decomposability, an algorithm for constructing the transformation matrix, a hierarchical RL algorithm, and robustness analysis when the design is applied to non-homogeneous MAS are presented. Simulations show that the proposed approach can guarantee significant speed-up in learning without any loss in the cumulative value of the LQR cost.

Model-Free Optimal Control of Linear Multi-Agent Systems via Decomposition and Hierarchical Approximation

Designing the optimal linear quadratic regulator (LQR) for a large-scale multi-agent system (MAS) is time-consuming since it involves solving a large-size matrix Riccati equation. The situation is further exasperated when the design needs to be done in a model-free way using schemes such as reinforcement learning (RL). To reduce this computational complexity, we decompose the large-scale LQR design problem into multiple sets of smaller-size LQR design problems. We consider the objective function to be specified over an undirected graph, and cast the decomposition as a graph clustering problem. The graph is decomposed into two parts, one consisting of multiple decoupled subgroups of connected components, and the other containing edges that connect the different subgroups. Accordingly, the resulting controller has a hierarchical structure, consisting of two components. The first component optimizes the performance of each decoupled subgroup by solving the smaller-size LQR design problem in a model-free way using an RL algorithm. The second component accounts for the objective coupling different subgroups, which is achieved by solving a least squares problem in one shot. Although suboptimal, the hierarchical controller adheres to a particular structure as specified by the inter-agent coupling in the objective function and by the decomposition strategy. Mathematical formulations are established to find a decomposition that minimizes required communication links or reduces the optimality gap. Numerical simulations are provided to highlight the pros and cons of the proposed designs.

A Decentralized Approach to Bayesian Learning

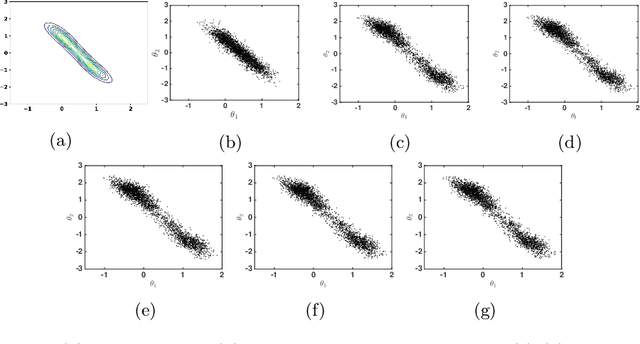
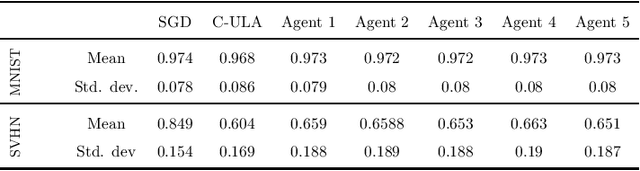
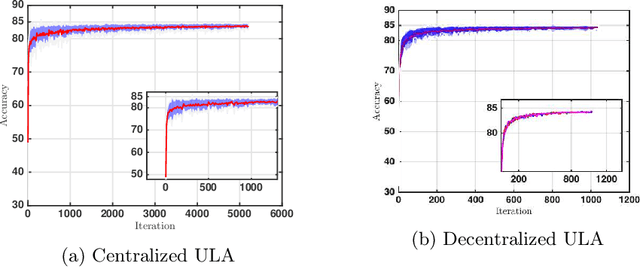
Motivated by decentralized approaches to machine learning, we propose a collaborative Bayesian learning algorithm taking the form of decentralized Langevin dynamics in a non-convex setting. Our analysis show that the initial KL-divergence between the Markov Chain and the target posterior distribution is exponentially decreasing while the error contributions to the overall KL-divergence from the additive noise is decreasing in polynomial time. We further show that the polynomial-term experiences speed-up with number of agents and provide sufficient conditions on the time-varying step-sizes to guarantee convergence to the desired distribution. The performance of the proposed algorithm is evaluated on a wide variety of machine learning tasks. The empirical results show that the performance of individual agents with locally available data is on par with the centralized setting with considerable improvement in the convergence rate.