A Decentralized Approach to Bayesian Learning
Paper and Code
Jul 14, 2020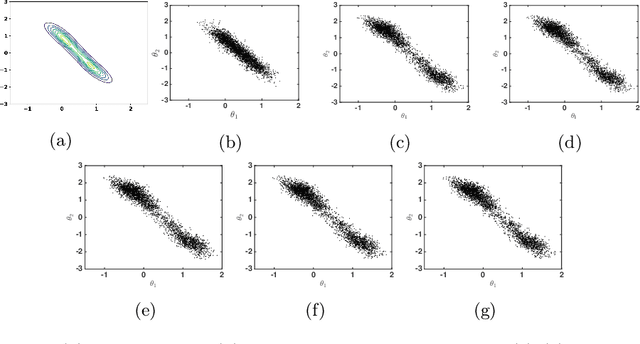
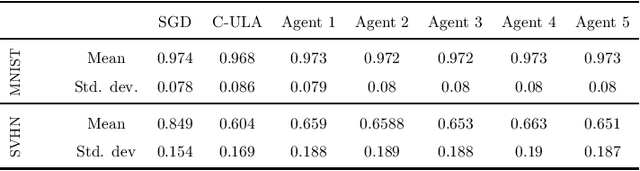
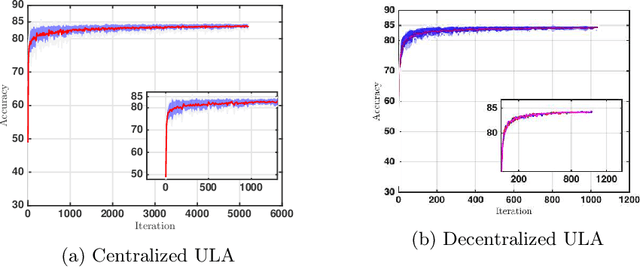
Motivated by decentralized approaches to machine learning, we propose a collaborative Bayesian learning algorithm taking the form of decentralized Langevin dynamics in a non-convex setting. Our analysis show that the initial KL-divergence between the Markov Chain and the target posterior distribution is exponentially decreasing while the error contributions to the overall KL-divergence from the additive noise is decreasing in polynomial time. We further show that the polynomial-term experiences speed-up with number of agents and provide sufficient conditions on the time-varying step-sizes to guarantee convergence to the desired distribution. The performance of the proposed algorithm is evaluated on a wide variety of machine learning tasks. The empirical results show that the performance of individual agents with locally available data is on par with the centralized setting with considerable improvement in the convergence rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge