Review of Recent Advances in Gaussian Process Regression Methods

Gaussian process (GP) methods have been widely studied recently, especially for large-scale systems with big data and even more extreme cases when data is sparse. Key advantages of these methods consist in: 1) the ability to provide inherent ways to assess the impact of uncertainties (especially in the data, and environment) on the solutions, 2) have efficient factorisation based implementations and 3) can be implemented easily in distributed manners and hence provide scalable solutions. This paper reviews the recently developed key factorised GP methods such as the hierarchical off-diagonal low-rank approximation methods and GP with Kronecker structures. An example illustrates the performance of these methods with respect to accuracy and computational complexity.

Gaussian Process Upper Confidence Bounds in Distributed Point Target Tracking over Wireless Sensor Networks

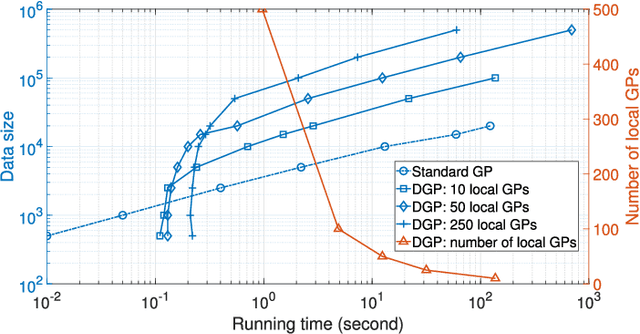
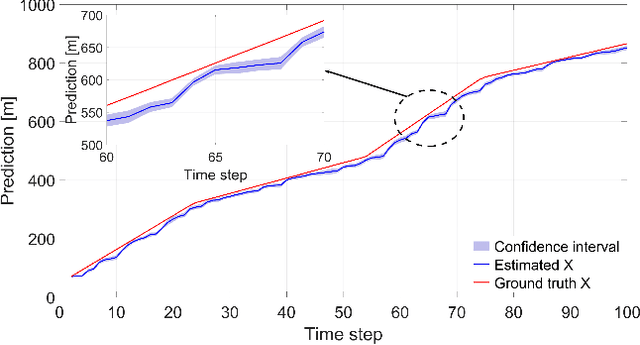
Uncertainty quantification plays a key role in the development of autonomous systems, decision-making, and tracking over wireless sensor networks (WSNs). However, there is a need of providing uncertainty confidence bounds, especially for distributed machine learning-based tracking, dealing with different volumes of data collected by sensors. This paper aims to fill in this gap and proposes a distributed Gaussian process (DGP) approach for point target tracking and derives upper confidence bounds (UCBs) of the state estimates. A unique contribution of this paper includes the derived theoretical guarantees on the proposed approach and its maximum accuracy for tracking with and without clutter measurements. Particularly, the developed approaches with uncertainty bounds are generic and can provide trustworthy solutions with an increased level of reliability. A novel hybrid Bayesian filtering method is proposed to enhance the DGP approach by adopting a Poisson measurement likelihood model. The proposed approaches are validated over a WSN case study, where sensors have limited sensing ranges. Numerical results demonstrate the tracking accuracy and robustness of the proposed approaches. The derived UCBs constitute a tool for trustworthiness evaluation of DGP approaches. The simulation results reveal that the proposed UCBs successfully encompass the true target states with 88% and 42% higher probability in X and Y coordinates, respectively, when compared to the confidence interval-based method.

Out-of-distribution Object Detection through Bayesian Uncertainty Estimation

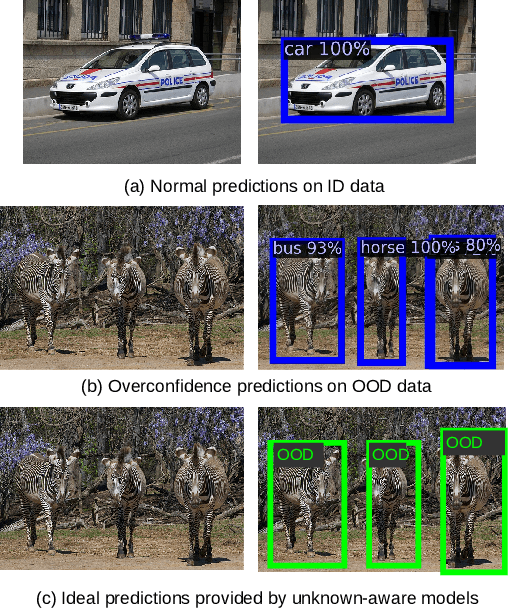
The superior performance of object detectors is often established under the condition that the test samples are in the same distribution as the training data. However, in many practical applications, out-of-distribution (OOD) instances are inevitable and usually lead to uncertainty in the results. In this paper, we propose a novel, intuitive, and scalable probabilistic object detection method for OOD detection. Unlike other uncertainty-modeling methods that either require huge computational costs to infer the weight distributions or rely on model training through synthetic outlier data, our method is able to distinguish between in-distribution (ID) data and OOD data via weight parameter sampling from proposed Gaussian distributions based on pre-trained networks. We demonstrate that our Bayesian object detector can achieve satisfactory OOD identification performance by reducing the FPR95 score by up to 8.19% and increasing the AUROC score by up to 13.94% when trained on BDD100k and VOC datasets as the ID datasets and evaluated on COCO2017 dataset as the OOD dataset.

Robust Learning via Ensemble Density Propagation in Deep Neural Networks

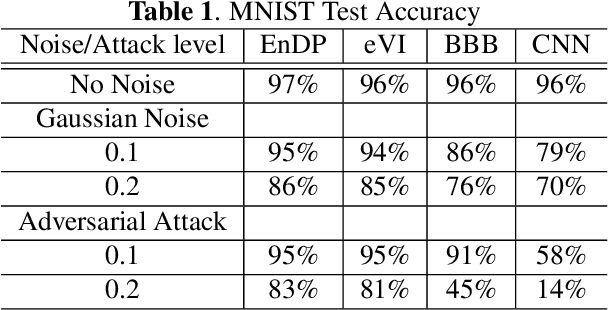
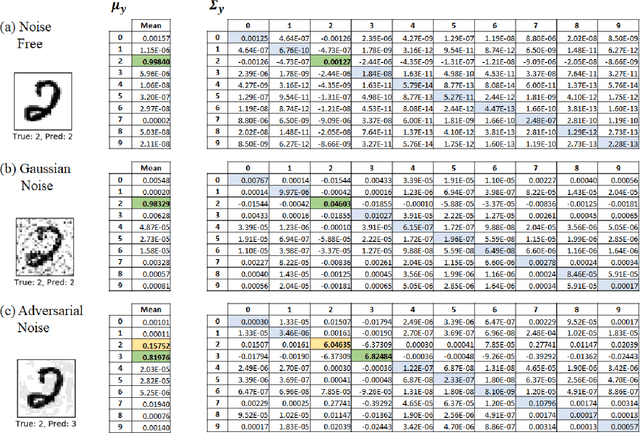
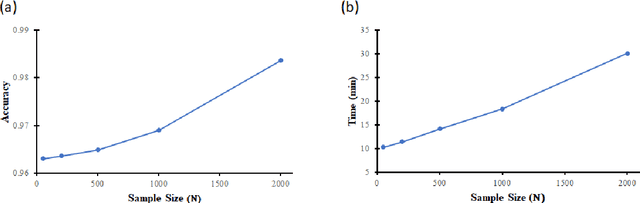
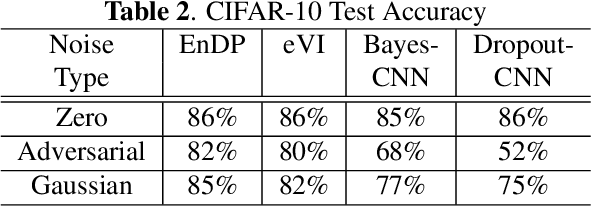
Learning in uncertain, noisy, or adversarial environments is a challenging task for deep neural networks (DNNs). We propose a new theoretically grounded and efficient approach for robust learning that builds upon Bayesian estimation and Variational Inference. We formulate the problem of density propagation through layers of a DNN and solve it using an Ensemble Density Propagation (EnDP) scheme. The EnDP approach allows us to propagate moments of the variational probability distribution across the layers of a Bayesian DNN, enabling the estimation of the mean and covariance of the predictive distribution at the output of the model. Our experiments using MNIST and CIFAR-10 datasets show a significant improvement in the robustness of the trained models to random noise and adversarial attacks.

Scalable Learning With a Structural Recurrent Neural Network for Short-Term Traffic Prediction

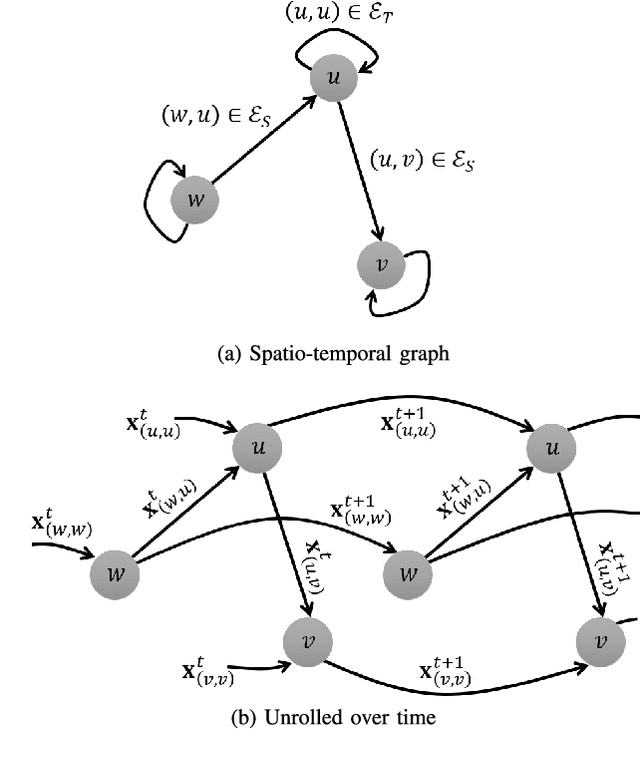
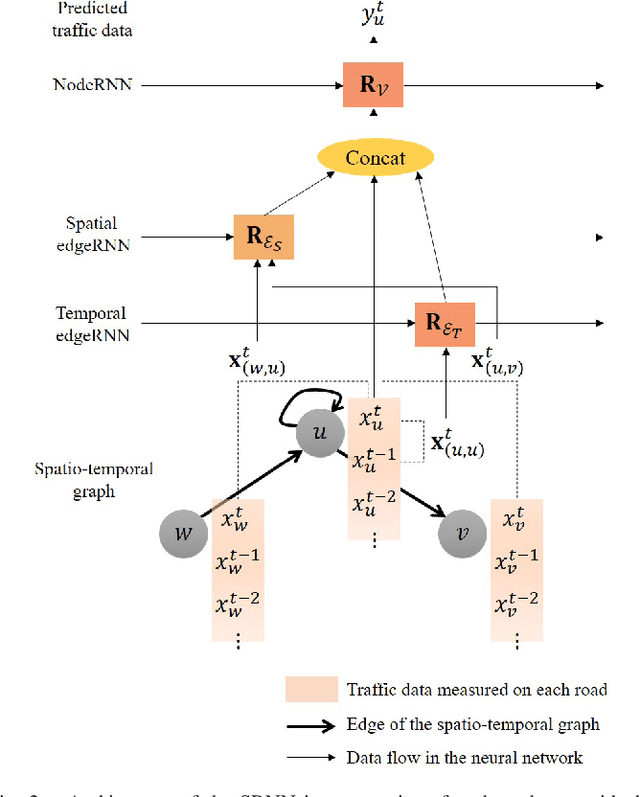
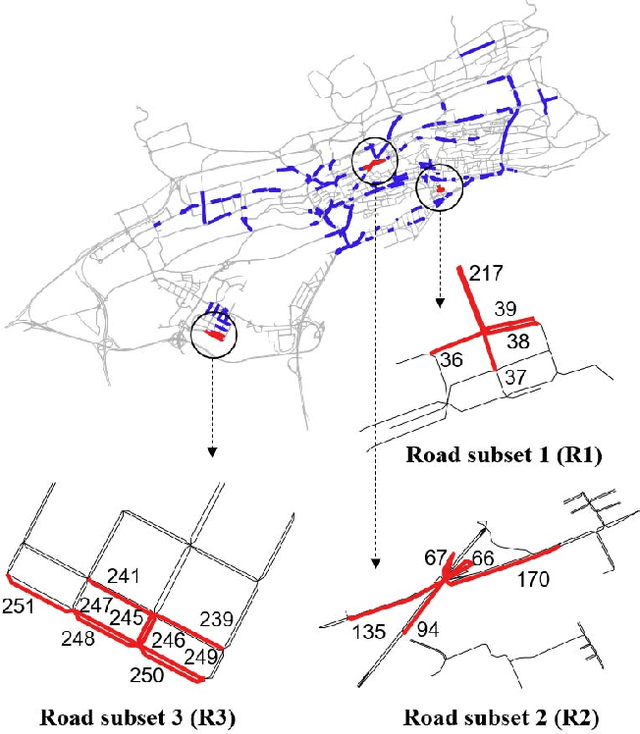
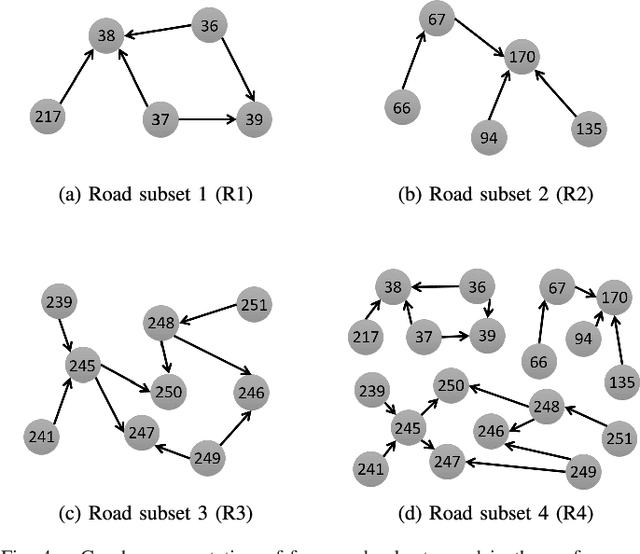
This paper presents a scalable deep learning approach for short-term traffic prediction based on historical traffic data in a vehicular road network. Capturing the spatio-temporal relationship of the big data often requires a significant amount of computational burden or an ad-hoc design aiming for a specific type of road network. To tackle the problem, we combine a road network graph with recurrent neural networks (RNNs) to construct a structural RNN (SRNN). The SRNN employs a spatio-temporal graph to infer the interaction between adjacent road segments as well as the temporal dynamics of the time series data. The model is scalable thanks to two key aspects. First, the proposed SRNN architecture is built by using the semantic similarity of the spatio-temporal dynamic interactions of all segments. Second, we design the architecture to deal with fixed-length tensors regardless of the graph topology. With the real traffic speed data measured in the city of Santander, we demonstrate the proposed SRNN outperforms the image-based approaches using the capsule network (CapsNet) by 14.1% and the convolutional neural network (CNN) by 5.87%, respectively, in terms of root mean squared error (RMSE). Moreover, we show that the proposed model is scalable. The SRNN model trained with data of a road network is able to predict traffic speed of different road networks, with the fixed number of parameters to train.

Variational Bayesian inference of hidden stochastic processes with unknown parameters

Estimating hidden processes from non-linear noisy observations is particularly difficult when the parameters of these processes are not known. This paper adopts a machine learning approach to devise variational Bayesian inference for such scenarios. In particular, a random process generated by the autoregressive moving average (ARMA) linear model is inferred from non-linearity noise observations. The posterior distribution of hidden states are approximated by a set of weighted particles generated by the sequential Monte carlo (SMC) algorithm involving sampling with importance sampling resampling (SISR). Numerical efficiency and estimation accuracy of the proposed inference method are evaluated by computer simulations. Furthermore, the proposed inference method is demonstrated on a practical problem of estimating the missing values in the gene expression time series assuming vector autoregressive (VAR) data model.

Structural Recurrent Neural Network for Traffic Speed Prediction

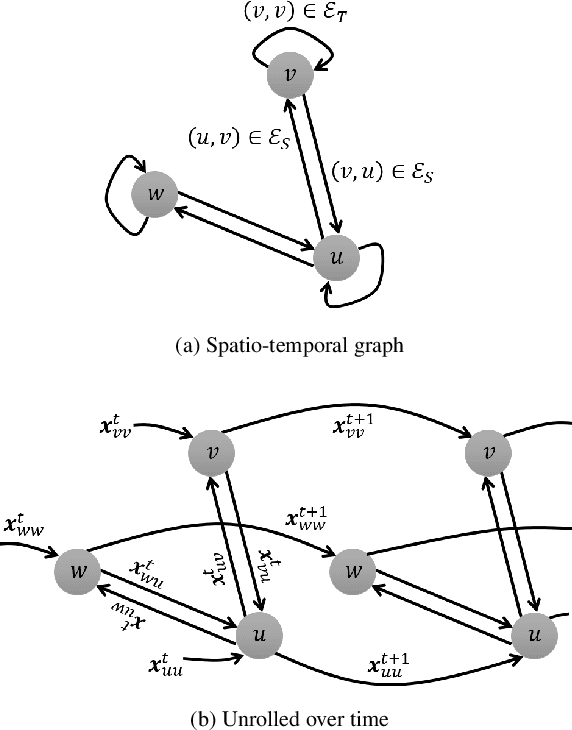
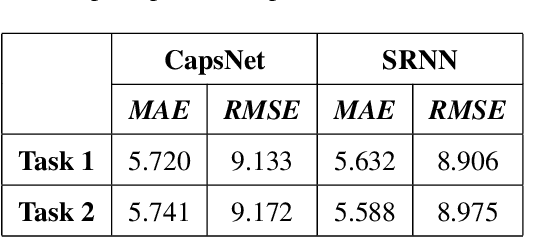
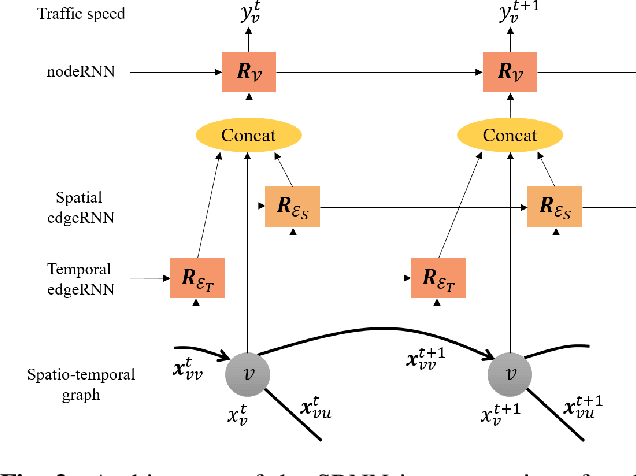
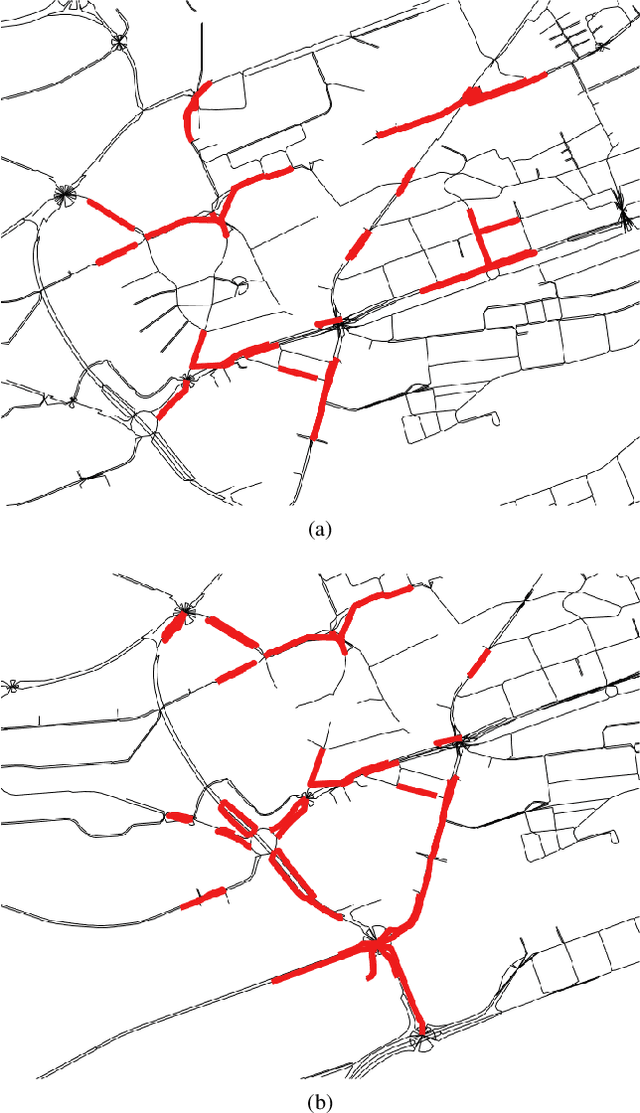
Deep neural networks have recently demonstrated the traffic prediction capability with the time series data obtained by sensors mounted on road segments. However, capturing spatio-temporal features of the traffic data often requires a significant number of parameters to train, increasing computational burden. In this work we demonstrate that embedding topological information of the road network improves the process of learning traffic features. We use a graph of a vehicular road network with recurrent neural networks (RNNs) to infer the interaction between adjacent road segments as well as the temporal dynamics. The topology of the road network is converted into a spatio-temporal graph to form a structural RNN (SRNN). The proposed approach is validated over traffic speed data from the road network of the city of Santander in Spain. The experiment shows that the graph-based method outperforms the state-of-the-art methods based on spatio-temporal images, requiring much fewer parameters to train.

Uncertainty propagation in neural networks for sparse coding

A novel method to propagate uncertainty through the soft-thresholding nonlinearity is proposed in this paper. At every layer the current distribution of the target vector is represented as a spike and slab distribution, which represents the probabilities of each variable being zero, or Gaussian-distributed. Using the proposed method of uncertainty propagation, the gradients of the logarithms of normalisation constants are derived, that can be used to update a weight distribution. A novel Bayesian neural network for sparse coding is designed utilising both the proposed method of uncertainty propagation and Bayesian inference algorithm.

A Capsule Network for Traffic Speed Prediction in Complex Road Networks

This paper proposes a deep learning approach for traffic flow prediction in complex road networks. Traffic flow data from induction loop sensors are essentially a time series, which is also spatially related to traffic in different road segments. The spatio-temporal traffic data can be converted into an image where the traffic data are expressed in a 3D space with respect to space and time axes. Although convolutional neural networks (CNNs) have been showing surprising performance in understanding images, they have a major drawback. In the max pooling operation, CNNs are losing important information by locally taking the highest activation values. The inter-relationship in traffic data measured by sparsely located sensors in different time intervals should not be neglected in order to obtain accurate predictions. Thus, we propose a neural network with capsules that replaces max pooling by dynamic routing. This is the first approach that employs the capsule network on a time series forecasting problem, to our best knowledge. Moreover, an experiment on real traffic speed data measured in the Santander city of Spain demonstrates the proposed method outperforms the state-of-the-art method based on a CNN by 13.1% in terms of root mean squared error.

Spatio-Temporal Structured Sparse Regression with Hierarchical Gaussian Process Priors

This paper introduces a new sparse spatio-temporal structured Gaussian process regression framework for online and offline Bayesian inference. This is the first framework that gives a time-evolving representation of the interdependencies between the components of the sparse signal of interest. A hierarchical Gaussian process describes such structure and the interdependencies are represented via the covariance matrices of the prior distributions. The inference is based on the expectation propagation method and the theoretical derivation of the posterior distribution is provided in the paper. The inference framework is thoroughly evaluated over synthetic, real video and electroencephalography (EEG) data where the spatio-temporal evolving patterns need to be reconstructed with high accuracy. It is shown that it achieves 15% improvement of the F-measure compared with the alternating direction method of multipliers, spatio-temporal sparse Bayesian learning method and one-level Gaussian process model. Additionally, the required memory for the proposed algorithm is less than in the one-level Gaussian process model. This structured sparse regression framework is of broad applicability to source localisation and object detection problems with sparse signals.