Deep Imbalanced Multi-Target Regression: 3D Point Cloud Voxel Content Estimation in Simulated Forests

Voxelization is an effective approach to reduce the computational cost of processing Light Detection and Ranging (LiDAR) data, yet it results in a loss of fine-scale structural information. This study explores whether low-level voxel content information, specifically target occupancy percentage within a voxel, can be inferred from high-level voxelized LiDAR point cloud data collected from Digital Imaging and remote Sensing Image Generation (DIRSIG) software. In our study, the targets include bark, leaf, soil, and miscellaneous materials. We propose a multi-target regression approach in the context of imbalanced learning using Kernel Point Convolutions (KPConv). Our research leverages cost-sensitive learning to address class imbalance called density-based relevance (DBR). We employ weighted Mean Saquared Erorr (MSE), Focal Regression (FocalR), and regularization to improve the optimization of KPConv. This study performs a sensitivity analysis on the voxel size (0.25 - 2 meters) to evaluate the effect of various grid representations in capturing the nuances of the forest. This sensitivity analysis reveals that larger voxel sizes (e.g., 2 meters) result in lower errors due to reduced variability, while smaller voxel sizes (e.g., 0.25 or 0.5 meter) exhibit higher errors, particularly within the canopy, where variability is greatest. For bark and leaf targets, error values at smaller voxel size datasets (0.25 and 0.5 meter) were significantly higher than those in larger voxel size datasets (2 meters), highlighting the difficulty in accurately estimating within-canopy voxel content at fine resolutions. This suggests that the choice of voxel size is application-dependent. Our work fills the gap in deep imbalance learning models for multi-target regression and simulated datasets for 3D LiDAR point clouds of forests.

Trustworthy Medical Segmentation with Uncertainty Estimation

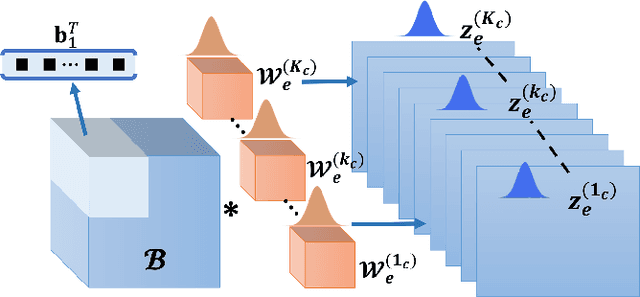
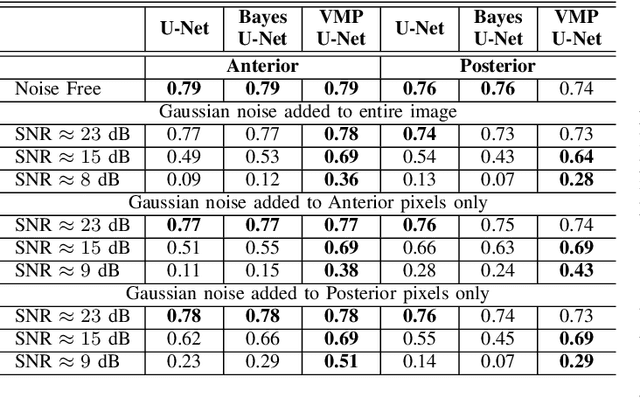
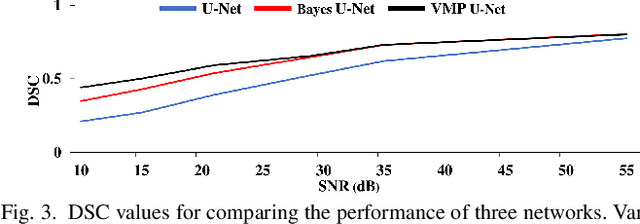
Deep Learning (DL) holds great promise in reshaping the healthcare systems given its precision, efficiency, and objectivity. However, the brittleness of DL models to noisy and out-of-distribution inputs is ailing their deployment in the clinic. Most systems produce point estimates without further information about model uncertainty or confidence. This paper introduces a new Bayesian deep learning framework for uncertainty quantification in segmentation neural networks, specifically encoder-decoder architectures. The proposed framework uses the first-order Taylor series approximation to propagate and learn the first two moments (mean and covariance) of the distribution of the model parameters given the training data by maximizing the evidence lower bound. The output consists of two maps: the segmented image and the uncertainty map of the segmentation. The uncertainty in the segmentation decisions is captured by the covariance matrix of the predictive distribution. We evaluate the proposed framework on medical image segmentation data from Magnetic Resonances Imaging and Computed Tomography scans. Our experiments on multiple benchmark datasets demonstrate that the proposed framework is more robust to noise and adversarial attacks as compared to state-of-the-art segmentation models. Moreover, the uncertainty map of the proposed framework associates low confidence (or equivalently high uncertainty) to patches in the test input images that are corrupted with noise, artifacts or adversarial attacks. Thus, the model can self-assess its segmentation decisions when it makes an erroneous prediction or misses part of the segmentation structures, e.g., tumor, by presenting higher values in the uncertainty map.

Robust Learning via Ensemble Density Propagation in Deep Neural Networks

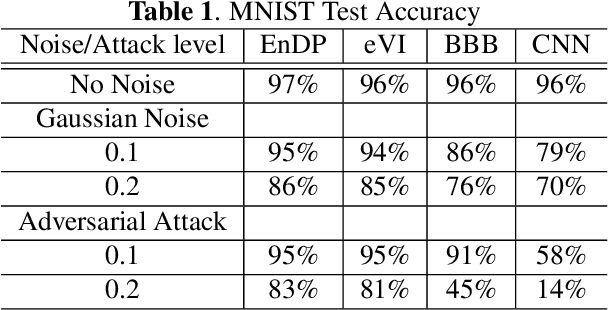
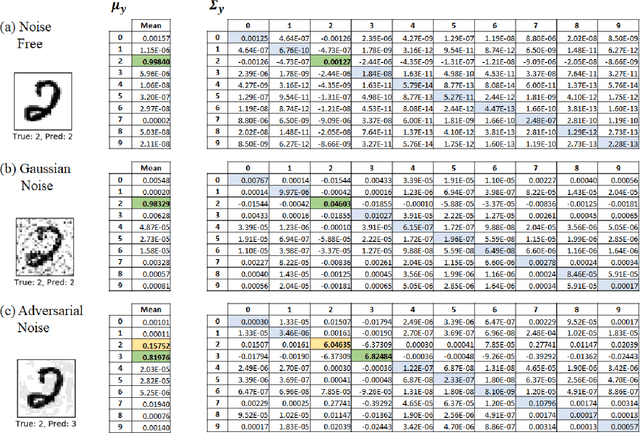
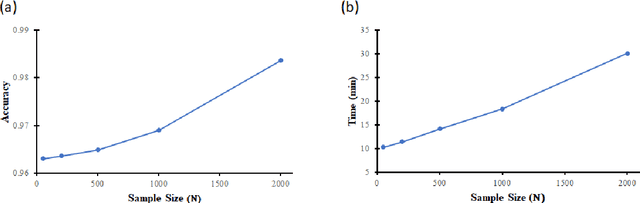
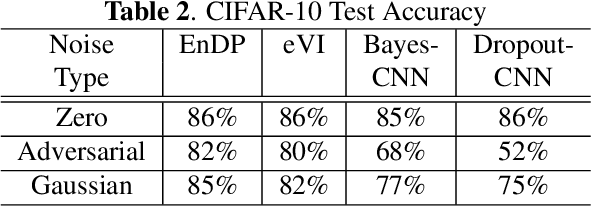
Learning in uncertain, noisy, or adversarial environments is a challenging task for deep neural networks (DNNs). We propose a new theoretically grounded and efficient approach for robust learning that builds upon Bayesian estimation and Variational Inference. We formulate the problem of density propagation through layers of a DNN and solve it using an Ensemble Density Propagation (EnDP) scheme. The EnDP approach allows us to propagate moments of the variational probability distribution across the layers of a Bayesian DNN, enabling the estimation of the mean and covariance of the predictive distribution at the output of the model. Our experiments using MNIST and CIFAR-10 datasets show a significant improvement in the robustness of the trained models to random noise and adversarial attacks.

Self-Compression in Bayesian Neural Networks

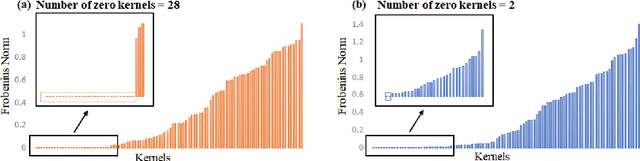
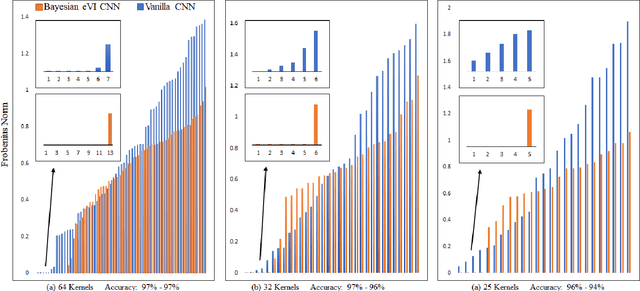
Machine learning models have achieved human-level performance on various tasks. This success comes at a high cost of computation and storage overhead, which makes machine learning algorithms difficult to deploy on edge devices. Typically, one has to partially sacrifice accuracy in favor of an increased performance quantified in terms of reduced memory usage and energy consumption. Current methods compress the networks by reducing the precision of the parameters or by eliminating redundant ones. In this paper, we propose a new insight into network compression through the Bayesian framework. We show that Bayesian neural networks automatically discover redundancy in model parameters, thus enabling self-compression, which is linked to the propagation of uncertainty through the layers of the network. Our experimental results show that the network architecture can be successfully compressed by deleting parameters identified by the network itself while retaining the same level of accuracy.

Robust Explainability: A Tutorial on Gradient-Based Attribution Methods for Deep Neural Networks

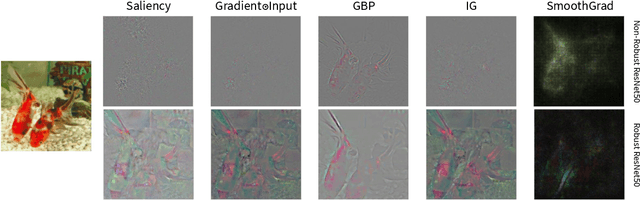
With the rise of deep neural networks, the challenge of explaining the predictions of these networks has become increasingly recognized. While many methods for explaining the decisions of deep neural networks exist, there is currently no consensus on how to evaluate them. On the other hand, robustness is a popular topic for deep learning research; however, it is hardly talked about in explainability until very recently. In this tutorial paper, we start by presenting gradient-based interpretability methods. These techniques use gradient signals to assign the burden of the decision on the input features. Later, we discuss how gradient-based methods can be evaluated for their robustness and the role that adversarial robustness plays in having meaningful explanations. We also discuss the limitations of gradient-based methods. Finally, we present the best practices and attributes that should be examined before choosing an explainability method. We conclude with the future directions for research in the area at the convergence of robustness and explainability.