Asynchronous Distributed Reinforcement Learning for LQR Control via Zeroth-Order Block Coordinate Descent
Paper and Code
Jul 28, 2021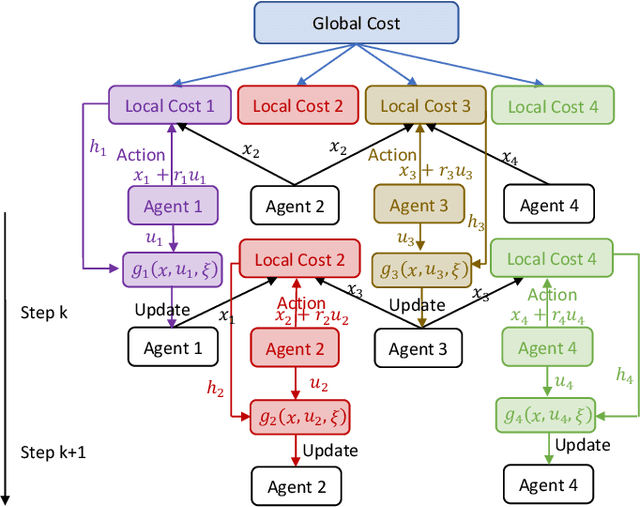
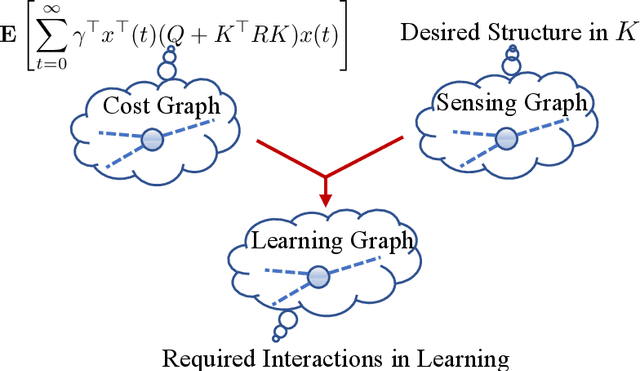
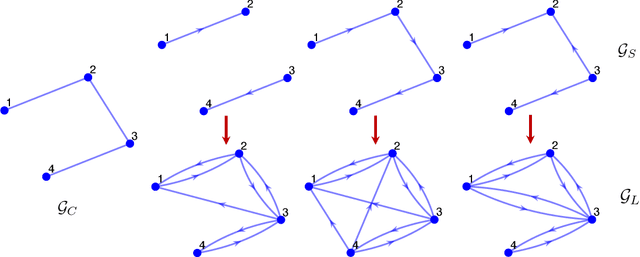
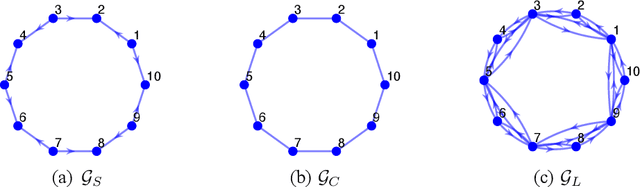
Recently introduced distributed zeroth-order optimization (ZOO) algorithms have shown their utility in distributed reinforcement learning (RL). Unfortunately, in the gradient estimation process, almost all of them require random samples with the same dimension as the global variable and/or require evaluation of the global cost function, which may induce high estimation variance for large-scale networks. In this paper, we propose a novel distributed zeroth-order algorithm by leveraging the network structure inherent in the optimization objective, which allows each agent to estimate its local gradient by local cost evaluation independently, without use of any consensus protocol. The proposed algorithm exhibits an asynchronous update scheme, and is designed for stochastic non-convex optimization with a possibly non-convex feasible domain based on the block coordinate descent method. The algorithm is later employed as a distributed model-free RL algorithm for distributed linear quadratic regulator design, where a learning graph is designed to describe the required interaction relationship among agents in distributed learning. We provide an empirical validation of the proposed algorithm to benchmark its performance on convergence rate and variance against a centralized ZOO algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge