A Scalable Graph-Theoretic Distributed Framework for Cooperative Multi-Agent Reinforcement Learning

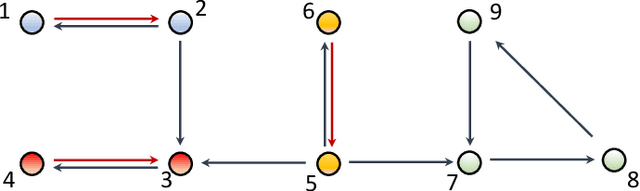
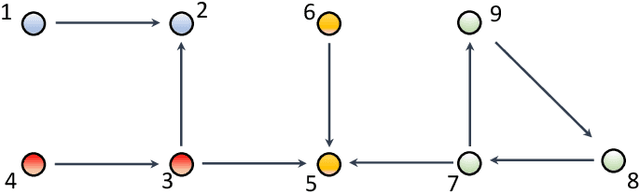
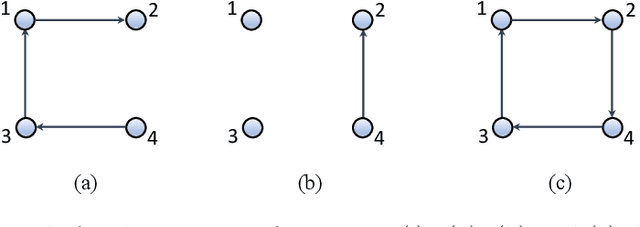
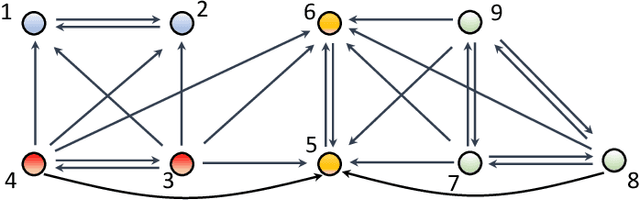
The main challenge of large-scale cooperative multi-agent reinforcement learning (MARL) is two-fold: (i) the RL algorithm is desired to be distributed due to limited resource for each individual agent; (ii) issues on convergence or computational complexity emerge due to the curse of dimensionality. Unfortunately, most of existing distributed RL references only focus on ensuring that the individual policy-seeking process of each agent is based on local information, but fail to solve the scalability issue induced by high dimensions of the state and action spaces when facing large-scale networks. In this paper, we propose a general distributed framework for cooperative MARL by utilizing the structures of graphs involved in this problem. We introduce three graphs in MARL, namely, the coordination graph, the observation graph and the reward graph. Based on these three graphs, and a given communication graph, we propose two distributed RL approaches. The first approach utilizes the inherent decomposability property of the problem itself, whose efficiency depends on the structures of the aforementioned four graphs, and is able to produce a high performance under specific graphical conditions. The second approach provides an approximate solution and is applicable for any graphs. Here the approximation error depends on an artificially designed index. The choice of this index is a trade-off between minimizing the approximation error and reducing the computational complexity. Simulations show that our RL algorithms have a significantly improved scalability to large-scale MASs compared with centralized and consensus-based distributed RL algorithms.

Distributed Cooperative Multi-Agent Reinforcement Learning with Directed Coordination Graph

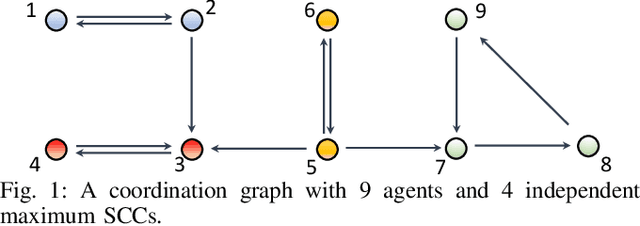
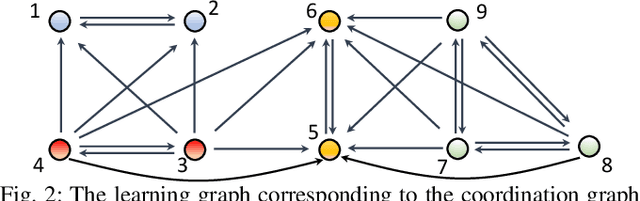
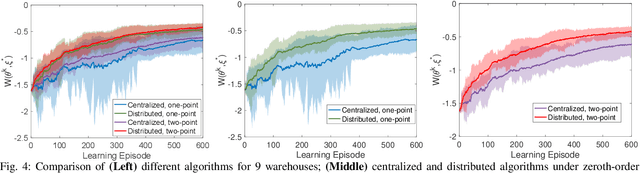
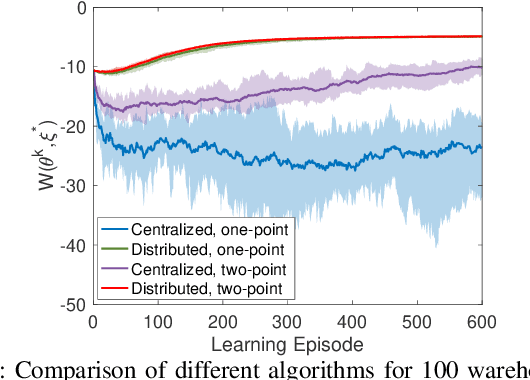
Existing distributed cooperative multi-agent reinforcement learning (MARL) frameworks usually assume undirected coordination graphs and communication graphs while estimating a global reward via consensus algorithms for policy evaluation. Such a framework may induce expensive communication costs and exhibit poor scalability due to requirement of global consensus. In this work, we study MARLs with directed coordination graphs, and propose a distributed RL algorithm where the local policy evaluations are based on local value functions. The local value function of each agent is obtained by local communication with its neighbors through a directed learning-induced communication graph, without using any consensus algorithm. A zeroth-order optimization (ZOO) approach based on parameter perturbation is employed to achieve gradient estimation. By comparing with existing ZOO-based RL algorithms, we show that our proposed distributed RL algorithm guarantees high scalability. A distributed resource allocation example is shown to illustrate the effectiveness of our algorithm.

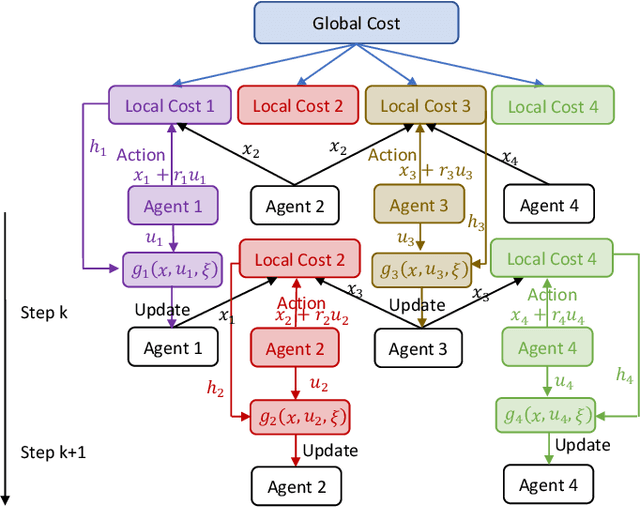
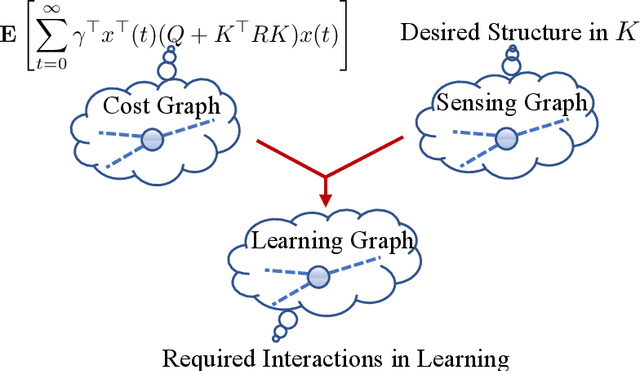
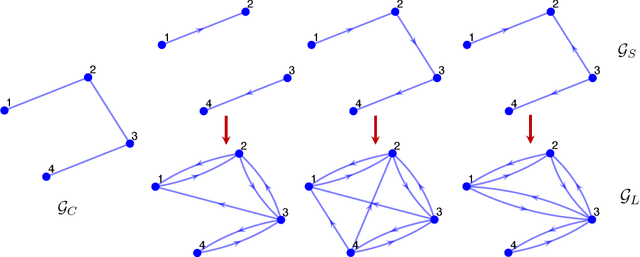
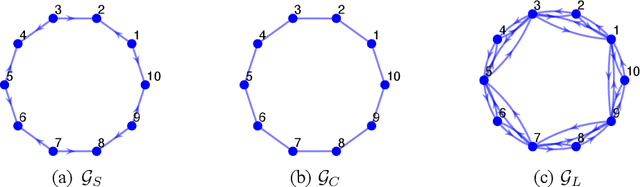
Asynchronous Distributed Reinforcement Learning for LQR Control via Zeroth-Order Block Coordinate Descent

Recently introduced distributed zeroth-order optimization (ZOO) algorithms have shown their utility in distributed reinforcement learning (RL). Unfortunately, in the gradient estimation process, almost all of them require random samples with the same dimension as the global variable and/or require evaluation of the global cost function, which may induce high estimation variance for large-scale networks. In this paper, we propose a novel distributed zeroth-order algorithm by leveraging the network structure inherent in the optimization objective, which allows each agent to estimate its local gradient by local cost evaluation independently, without use of any consensus protocol. The proposed algorithm exhibits an asynchronous update scheme, and is designed for stochastic non-convex optimization with a possibly non-convex feasible domain based on the block coordinate descent method. The algorithm is later employed as a distributed model-free RL algorithm for distributed linear quadratic regulator design, where a learning graph is designed to describe the required interaction relationship among agents in distributed learning. We provide an empirical validation of the proposed algorithm to benchmark its performance on convergence rate and variance against a centralized ZOO algorithm.

Hierarchical Reinforcement Learning for Optimal Control of Linear Multi-Agent Systems: the Homogeneous Case

Individual agents in a multi-agent system (MAS) may have decoupled open-loop dynamics, but a cooperative control objective usually results in coupled closed-loop dynamics thereby making the control design computationally expensive. The computation time becomes even higher when a learning strategy such as reinforcement learning (RL) needs to be applied to deal with the situation when the agents dynamics are not known. To resolve this problem, this paper proposes a hierarchical RL scheme for a linear quadratic regulator (LQR) design in a continuous-time linear MAS. The idea is to exploit the structural properties of two graphs embedded in the $Q$ and $R$ weighting matrices in the LQR objective to define an orthogonal transformation that can convert the original LQR design to multiple decoupled smaller-sized LQR designs. We show that if the MAS is homogeneous then this decomposition retains closed-loop optimality. Conditions for decomposability, an algorithm for constructing the transformation matrix, a hierarchical RL algorithm, and robustness analysis when the design is applied to non-homogeneous MAS are presented. Simulations show that the proposed approach can guarantee significant speed-up in learning without any loss in the cumulative value of the LQR cost.

Model-Free Optimal Control of Linear Multi-Agent Systems via Decomposition and Hierarchical Approximation

Designing the optimal linear quadratic regulator (LQR) for a large-scale multi-agent system (MAS) is time-consuming since it involves solving a large-size matrix Riccati equation. The situation is further exasperated when the design needs to be done in a model-free way using schemes such as reinforcement learning (RL). To reduce this computational complexity, we decompose the large-scale LQR design problem into multiple sets of smaller-size LQR design problems. We consider the objective function to be specified over an undirected graph, and cast the decomposition as a graph clustering problem. The graph is decomposed into two parts, one consisting of multiple decoupled subgroups of connected components, and the other containing edges that connect the different subgroups. Accordingly, the resulting controller has a hierarchical structure, consisting of two components. The first component optimizes the performance of each decoupled subgroup by solving the smaller-size LQR design problem in a model-free way using an RL algorithm. The second component accounts for the objective coupling different subgroups, which is achieved by solving a least squares problem in one shot. Although suboptimal, the hierarchical controller adheres to a particular structure as specified by the inter-agent coupling in the objective function and by the decomposition strategy. Mathematical formulations are established to find a decomposition that minimizes required communication links or reduces the optimality gap. Numerical simulations are provided to highlight the pros and cons of the proposed designs.