SQuARM-SGD: Communication-Efficient Momentum SGD for Decentralized Optimization

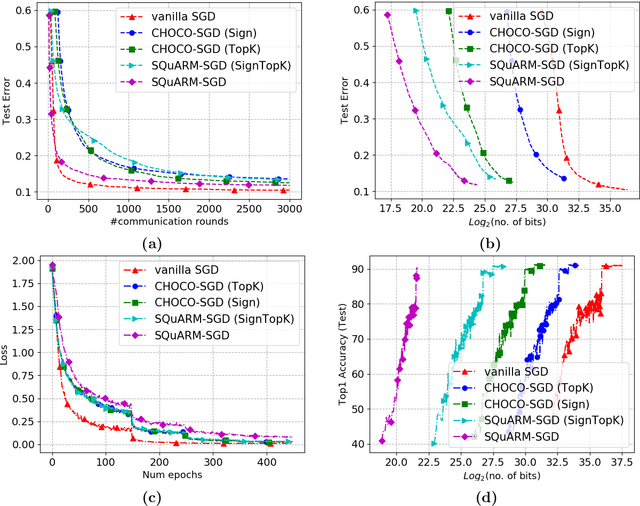
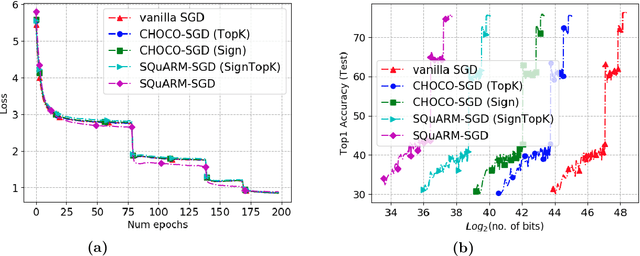
In this paper, we consider the problem of communication-efficient decentralized training of large-scale machine learning models over a network. We propose and analyze SQuARM-SGD, an algorithm for decentralized training, which employs {\em momentum} and {\em compressed communication} between nodes regulated by a locally computable triggering condition in stochastic gradient descent (SGD). In SQuARM-SGD, each node performs a fixed number of local SGD steps using Nesterov's momentum and then sends sparisified and quantized updates to its neighbors only when there is a significant change in the model parameters since the last time communication occurred. We provide convergence guarantees of our algorithm for (smooth) strongly convex and non-convex objectives, and show that SQuARM-SGD converges at a rate of $\mathcal{O}\left(\nicefrac{1}{nT}\right)$ for strongly convex objectives, while for non-convex objectives it convergences at a rate of $\mathcal{O}\left(\nicefrac{1}{\sqrt{nT}}\right)$, thus matching the convergence rate of \emph{vanilla} distributed SGD in both these settings. We corroborate our theoretical understanding with experiments and compare the performance of our algorithm with the state-of-the-art, showing that without sacrificing much on the accuracy, SQuARM-SGD converges at a similar rate while saving significantly in total communicated bits.