Differentially Private Consensus-Based Distributed Optimization
Paper and Code
Mar 19, 2019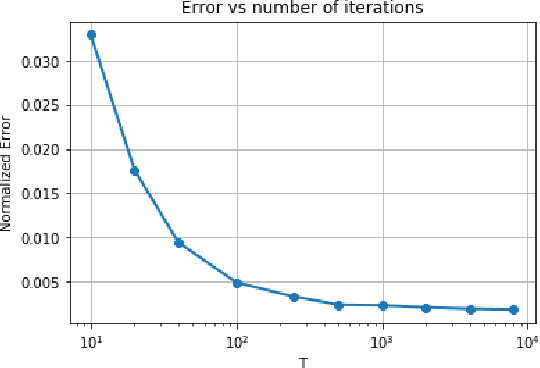
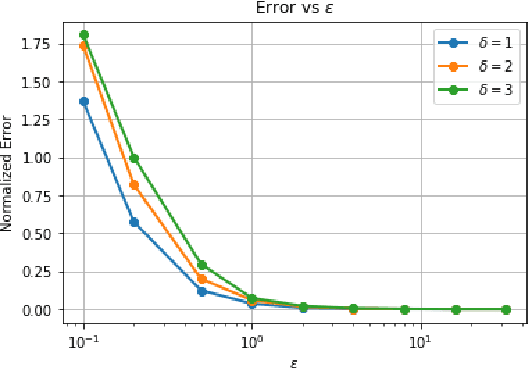

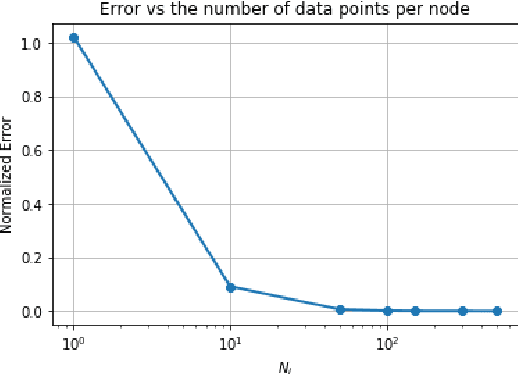
Data privacy is an important concern in learning, when datasets contain sensitive information about individuals. This paper considers consensus-based distributed optimization under data privacy constraints. Consensus-based optimization consists of a set of computational nodes arranged in a graph, each having a local objective that depends on their local data, where in every step nodes take a linear combination of their neighbors' messages, as well as taking a new gradient step. Since the algorithm requires exchanging messages that depend on local data, private information gets leaked at every step. Taking $(\epsilon, \delta)$-differential privacy (DP) as our criterion, we consider the strategy where the nodes add random noise to their messages before broadcasting it, and show that the method achieves convergence with a bounded mean-squared error, while satisfying $(\epsilon, \delta)$-DP. By relaxing the more stringent $\epsilon$-DP requirement in previous work, we strengthen a known convergence result in the literature. We conclude the paper with numerical results demonstrating the effectiveness of our methods for mean estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge