Differentially Private Consensus-Based Distributed Optimization

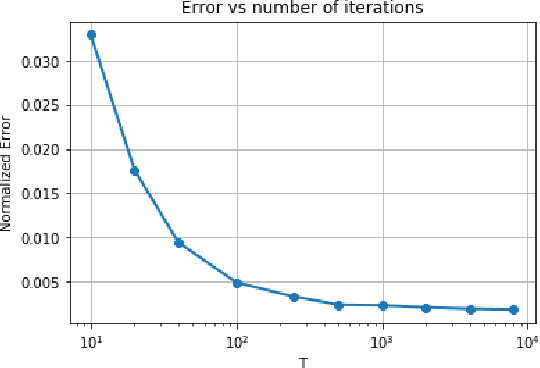
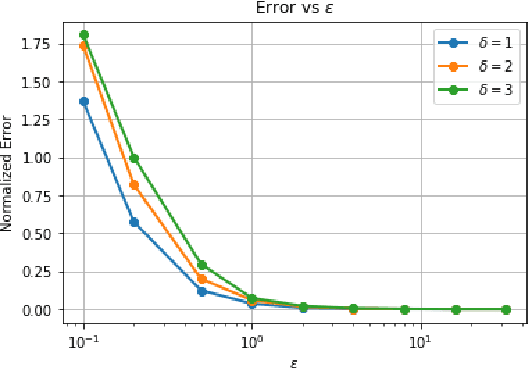
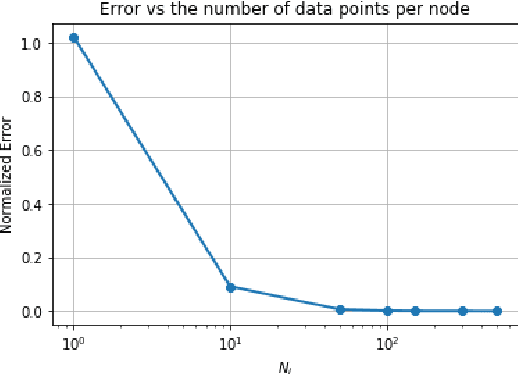
Data privacy is an important concern in learning, when datasets contain sensitive information about individuals. This paper considers consensus-based distributed optimization under data privacy constraints. Consensus-based optimization consists of a set of computational nodes arranged in a graph, each having a local objective that depends on their local data, where in every step nodes take a linear combination of their neighbors' messages, as well as taking a new gradient step. Since the algorithm requires exchanging messages that depend on local data, private information gets leaked at every step. Taking $(\epsilon, \delta)$-differential privacy (DP) as our criterion, we consider the strategy where the nodes add random noise to their messages before broadcasting it, and show that the method achieves convergence with a bounded mean-squared error, while satisfying $(\epsilon, \delta)$-DP. By relaxing the more stringent $\epsilon$-DP requirement in previous work, we strengthen a known convergence result in the literature. We conclude the paper with numerical results demonstrating the effectiveness of our methods for mean estimation.

Privacy-Utility Trade-off of Linear Regression under Random Projections and Additive Noise

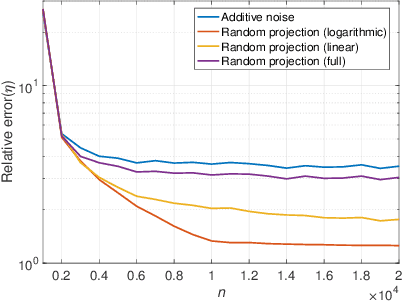
Data privacy is an important concern in machine learning, and is fundamentally at odds with the task of training useful learning models, which typically require the acquisition of large amounts of private user data. One possible way of fulfilling the machine learning task while preserving user privacy is to train the model on a transformed, noisy version of the data, which does not reveal the data itself directly to the training procedure. In this work, we analyze the privacy-utility trade-off of two such schemes for the problem of linear regression: additive noise, and random projections. In contrast to previous work, we consider a recently proposed notion of differential privacy that is based on conditional mutual information (MI-DP), which is stronger than the conventional $(\epsilon, \delta)$-differential privacy, and use relative objective error as the utility metric. We find that projecting the data to a lower-dimensional subspace before adding noise attains a better trade-off in general. We also make a connection between privacy problem and (non-coherent) SIMO, which has been extensively studied in wireless communication, and use tools from there for the analysis. We present numerical results demonstrating the performance of the schemes.