Extreme Stochastic Variational Inference: Distributed and Asynchronous
Paper and Code
Aug 03, 2018
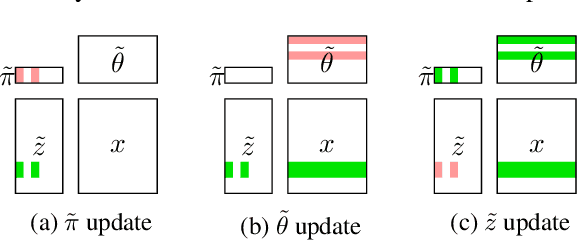
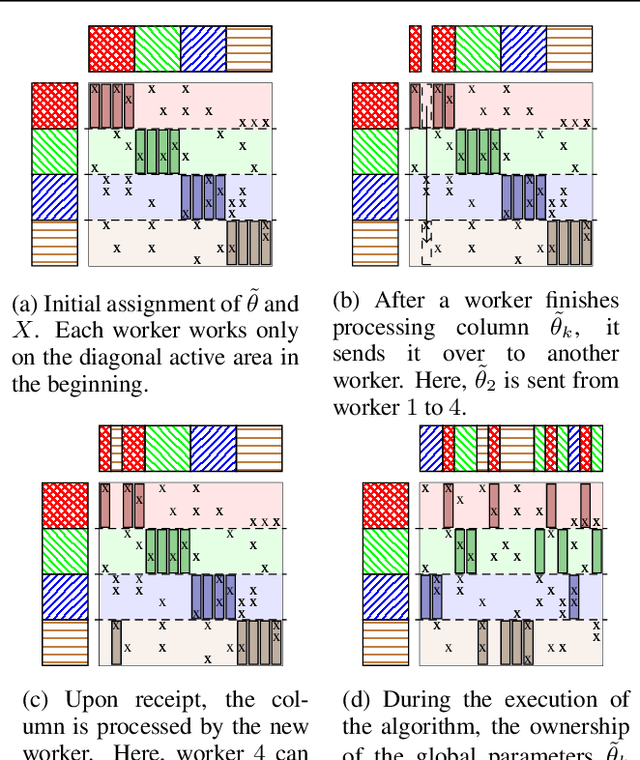
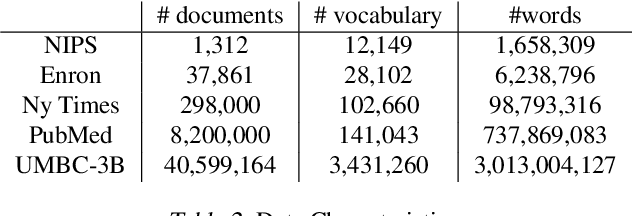
Stochastic variational inference (SVI), the state-of-the-art algorithm for scaling variational inference to large-datasets, is inherently serial. Moreover, it requires the parameters to fit in the memory of a single processor; this is problematic when the number of parameters is in billions. In this paper, we propose extreme stochastic variational inference (ESVI), an asynchronous and lock-free algorithm to perform variational inference for mixture models on massive real world datasets. ESVI overcomes the limitations of SVI by requiring that each processor only access a subset of the data and a subset of the parameters, thus providing data and model parallelism simultaneously. We demonstrate the effectiveness of ESVI by running Latent Dirichlet Allocation (LDA) on UMBC-3B, a dataset that has a vocabulary of 3 million and a token size of 3 billion. In our experiments, we found that ESVI not only outperforms VI and SVI in wallclock-time, but also achieves a better quality solution. In addition, we propose a strategy to speed up computation and save memory when fitting large number of topics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge