Bayesian Constraint Inference from User Demonstrations Based on Margin-Respecting Preference Models

It is crucial for robots to be aware of the presence of constraints in order to acquire safe policies. However, explicitly specifying all constraints in an environment can be a challenging task. State-of-the-art constraint inference algorithms learn constraints from demonstrations, but tend to be computationally expensive and prone to instability issues. In this paper, we propose a novel Bayesian method that infers constraints based on preferences over demonstrations. The main advantages of our proposed approach are that it 1) infers constraints without calculating a new policy at each iteration, 2) uses a simple and more realistic ranking of groups of demonstrations, without requiring pairwise comparisons over all demonstrations, and 3) adapts to cases where there are varying levels of constraint violation. Our empirical results demonstrate that our proposed Bayesian approach infers constraints of varying severity, more accurately than state-of-the-art constraint inference methods.

Constraint Inference in Control Tasks from Expert Demonstrations via Inverse Optimization

Inferring unknown constraints is a challenging and crucial problem in many robotics applications. When only expert demonstrations are available, it becomes essential to infer the unknown domain constraints to deploy additional agents effectively. In this work, we propose an approach to infer affine constraints in control tasks after observing expert demonstrations. We formulate the constraint inference problem as an inverse optimization problem, and we propose an alternating optimization scheme that infers the unknown constraints by minimizing a KKT residual objective. We demonstrate the effectiveness of our method in a number of simulations, and show that our method can infer less conservative constraints than a recent baseline method while maintaining comparable safety guarantees.

Data-Driven Low-Rank Neural Network Compression

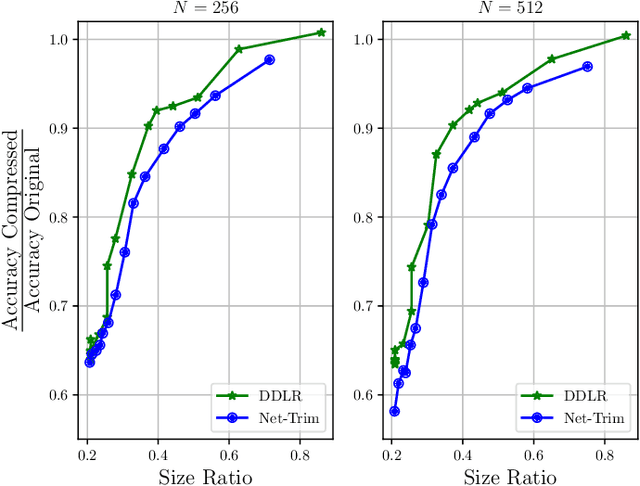
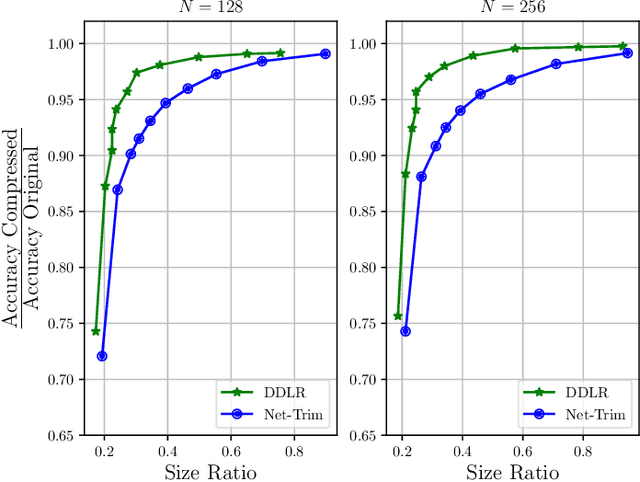
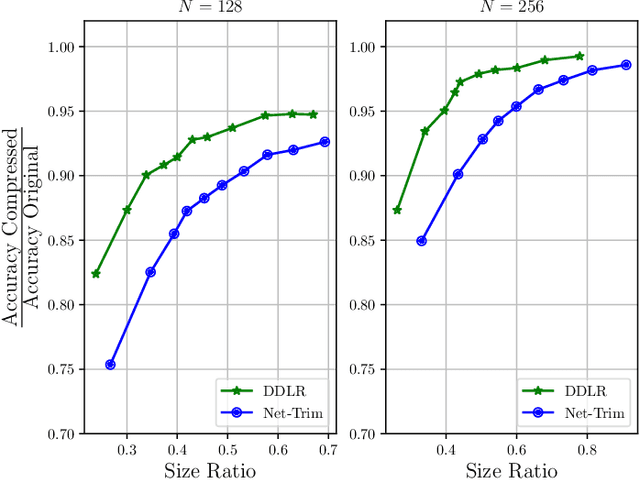
Despite many modern applications of Deep Neural Networks (DNNs), the large number of parameters in the hidden layers makes them unattractive for deployment on devices with storage capacity constraints. In this paper we propose a Data-Driven Low-rank (DDLR) method to reduce the number of parameters of pretrained DNNs and expedite inference by imposing low-rank structure on the fully connected layers, while controlling for the overall accuracy and without requiring any retraining. We pose the problem as finding the lowest rank approximation of each fully connected layer with given performance guarantees and relax it to a tractable convex optimization problem. We show that it is possible to significantly reduce the number of parameters in common DNN architectures with only a small reduction in classification accuracy. We compare DDLR with Net-Trim, which is another data-driven DNN compression technique based on sparsity and show that DDLR consistently produces more compressed neural networks while maintaining higher accuracy.

Control of Unknown Nonlinear Systems with Linear Time-Varying MPC

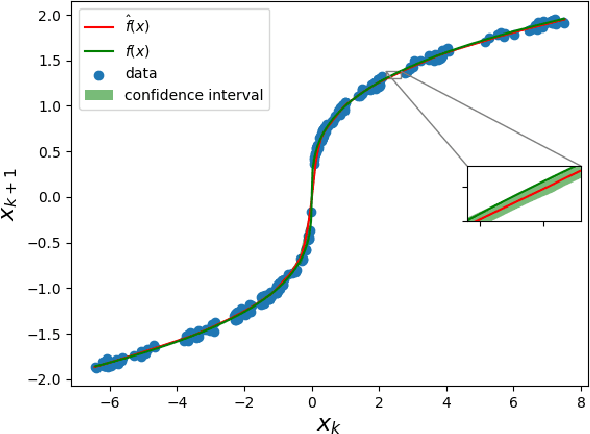
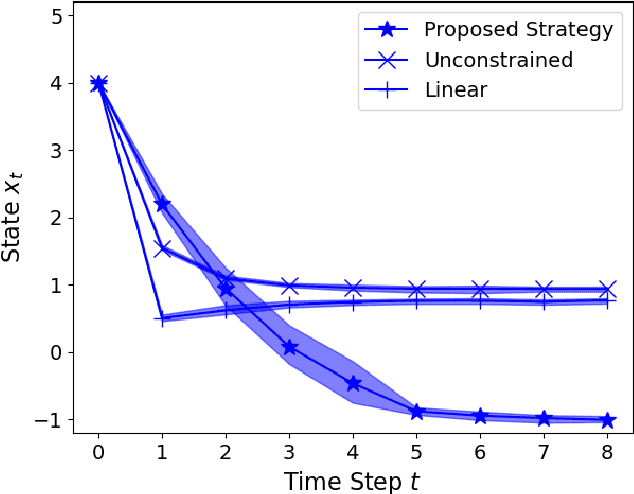
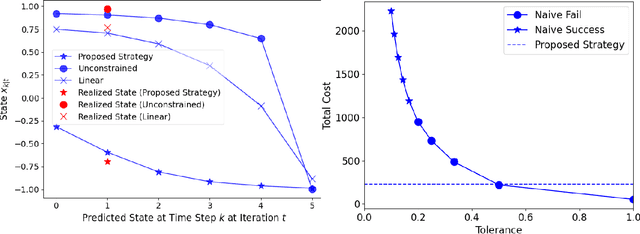
We present a Model Predictive Control (MPC) strategy for unknown input-affine nonlinear dynamical systems. A non-parametric method is used to estimate the nonlinear dynamics from observed data. The estimated nonlinear dynamics are then linearized over time varying regions of the state space to construct an Affine Time Varying (ATV) model. Error bounds arising from the estimation and linearization procedure are computed by using sampling techniques. The ATV model and the uncertainty sets are used to design a robust Model Predictive Control (MPC) problem which guarantees safety for the unknown system with high probability. A simple nonlinear example demonstrates the effectiveness of the approach where commonly used linearization methods fail.