Composition of Experts: A Modular Compound AI System Leveraging Large Language Models

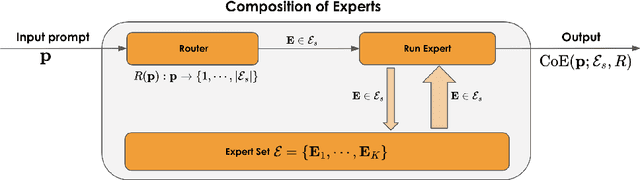
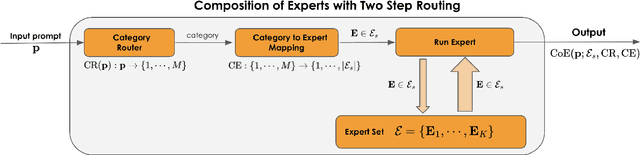
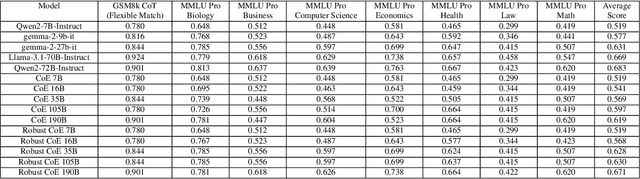
Large Language Models (LLMs) have achieved remarkable advancements, but their monolithic nature presents challenges in terms of scalability, cost, and customization. This paper introduces the Composition of Experts (CoE), a modular compound AI system leveraging multiple expert LLMs. CoE leverages a router to dynamically select the most appropriate expert for a given input, enabling efficient utilization of resources and improved performance. We formulate the general problem of training a CoE and discuss inherent complexities associated with it. We propose a two-step routing approach to address these complexities that first uses a router to classify the input into distinct categories followed by a category-to-expert mapping to obtain desired experts. CoE offers a flexible and cost-effective solution to build compound AI systems. Our empirical evaluation demonstrates the effectiveness of CoE in achieving superior performance with reduced computational overhead. Given that CoE comprises of many expert LLMs it has unique system requirements for cost-effective serving. We present an efficient implementation of CoE leveraging SambaNova SN40L RDUs unique three-tiered memory architecture. CoEs obtained using open weight LLMs Qwen/Qwen2-7B-Instruct, google/gemma-2-9b-it, google/gemma-2-27b-it, meta-llama/Llama-3.1-70B-Instruct and Qwen/Qwen2-72B-Instruct achieve a score of $59.4$ with merely $31$ billion average active parameters on Arena-Hard and a score of $9.06$ with $54$ billion average active parameters on MT-Bench.

Constructing Domain-Specific Evaluation Sets for LLM-as-a-judge

Large Language Models (LLMs) have revolutionized the landscape of machine learning, yet current benchmarks often fall short in capturing the diverse behavior of these models in real-world applications. A benchmark's usefulness is determined by its ability to clearly differentiate between models of varying capabilities (separability) and closely align with human preferences. Existing frameworks like Alpaca-Eval 2.0 LC \cite{dubois2024lengthcontrolledalpacaevalsimpleway} and Arena-Hard v0.1 \cite{li2024crowdsourced} are limited by their focus on general-purpose queries and lack of diversity across domains such as law, medicine, and multilingual contexts. In this paper, we address these limitations by introducing a novel data pipeline that curates diverse, domain-specific evaluation sets tailored for LLM-as-a-Judge frameworks. Our approach leverages a combination of manual curation, semi-supervised learning to generate clusters, and stratified sampling to ensure balanced representation across a wide range of domains and languages. The resulting evaluation set, which includes 1573 samples across 14 categories, demonstrates high separability (84\%) across ten top-ranked models, and agreement (84\%) with Chatbot Arena and (0.915) Spearman correlation. The agreement values are 9\% better than Arena Hard and 20\% better than AlpacaEval 2.0 LC, while the Spearman coefficient is 0.7 more than the next best benchmark, showcasing a significant improvement in the usefulness of the benchmark. We further provide an open-source evaluation tool that enables fine-grained analysis of model performance across user-defined categories, offering valuable insights for practitioners. This work contributes to the ongoing effort to enhance the transparency, diversity, and effectiveness of LLM evaluation methodologies.

SambaNova SN40L: Scaling the AI Memory Wall with Dataflow and Composition of Experts

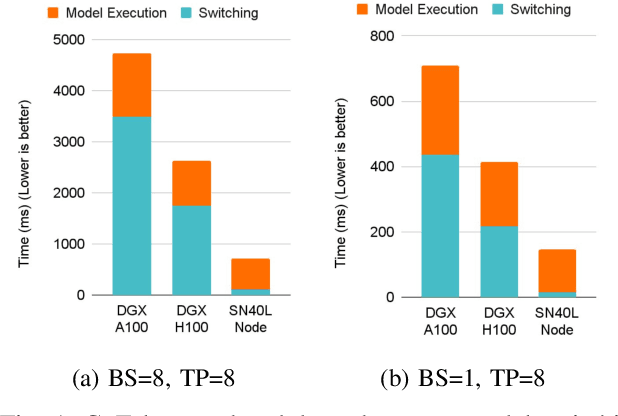
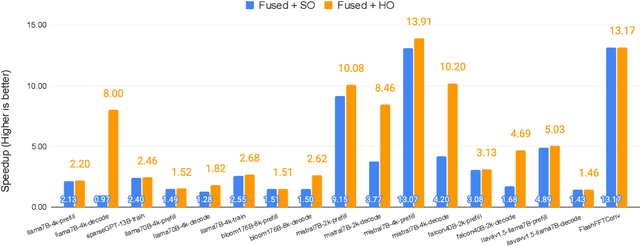
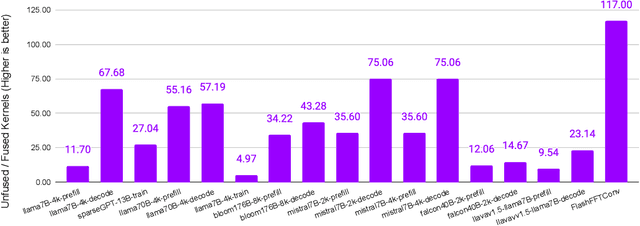
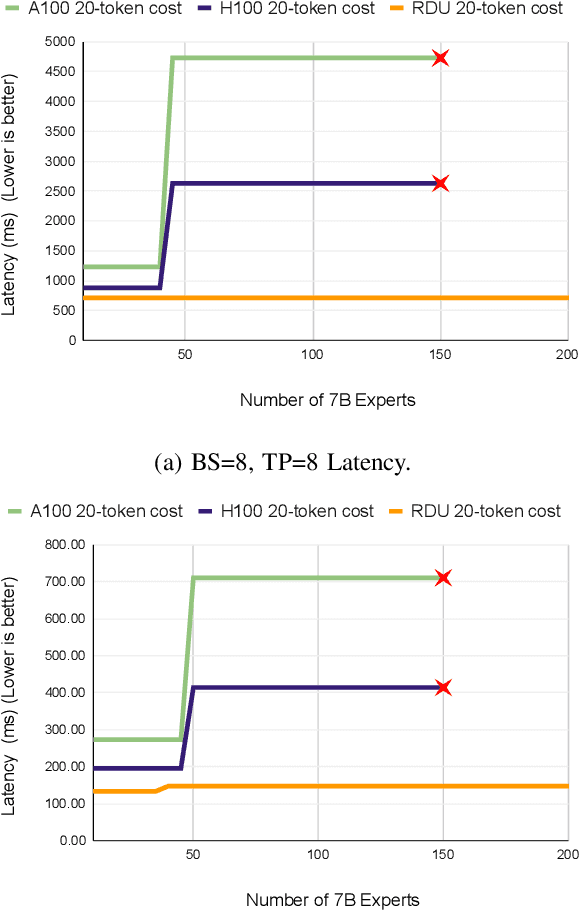
Monolithic large language models (LLMs) like GPT-4 have paved the way for modern generative AI applications. Training, serving, and maintaining monolithic LLMs at scale, however, remains prohibitively expensive and challenging. The disproportionate increase in compute-to-memory ratio of modern AI accelerators have created a memory wall, necessitating new methods to deploy AI. Composition of Experts (CoE) is an alternative modular approach that lowers the cost and complexity of training and serving. However, this approach presents two key challenges when using conventional hardware: (1) without fused operations, smaller models have lower operational intensity, which makes high utilization more challenging to achieve; and (2) hosting a large number of models can be either prohibitively expensive or slow when dynamically switching between them. In this paper, we describe how combining CoE, streaming dataflow, and a three-tier memory system scales the AI memory wall. We describe Samba-CoE, a CoE system with 150 experts and a trillion total parameters. We deploy Samba-CoE on the SambaNova SN40L Reconfigurable Dataflow Unit (RDU) - a commercial dataflow accelerator architecture that has been co-designed for enterprise inference and training applications. The chip introduces a new three-tier memory system with on-chip distributed SRAM, on-package HBM, and off-package DDR DRAM. A dedicated inter-RDU network enables scaling up and out over multiple sockets. We demonstrate speedups ranging from 2x to 13x on various benchmarks running on eight RDU sockets compared with an unfused baseline. We show that for CoE inference deployments, the 8-socket RDU Node reduces machine footprint by up to 19x, speeds up model switching time by 15x to 31x, and achieves an overall speedup of 3.7x over a DGX H100 and 6.6x over a DGX A100.

Data-Driven Low-Rank Neural Network Compression

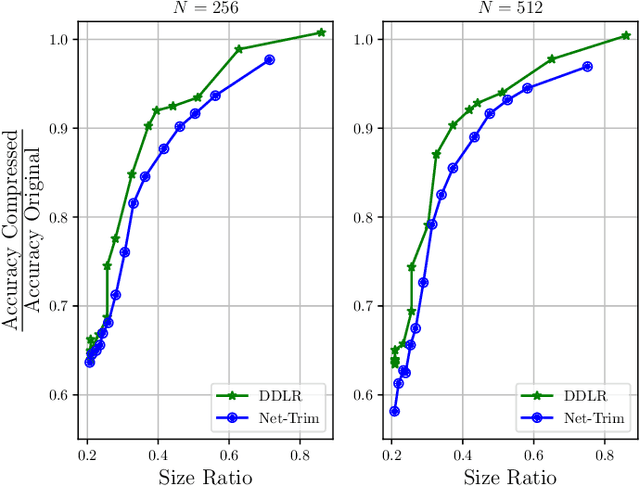
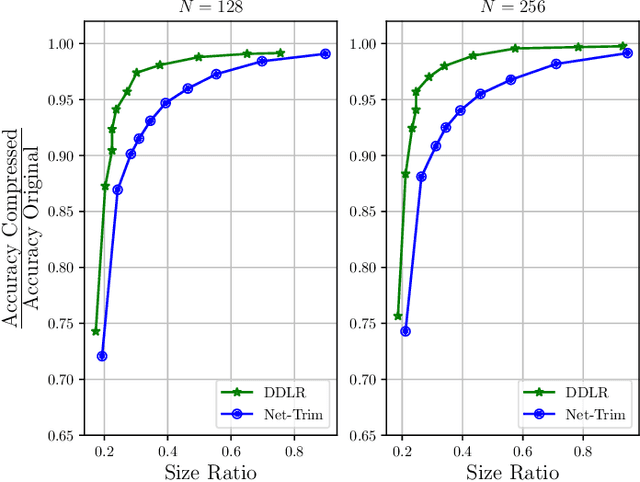
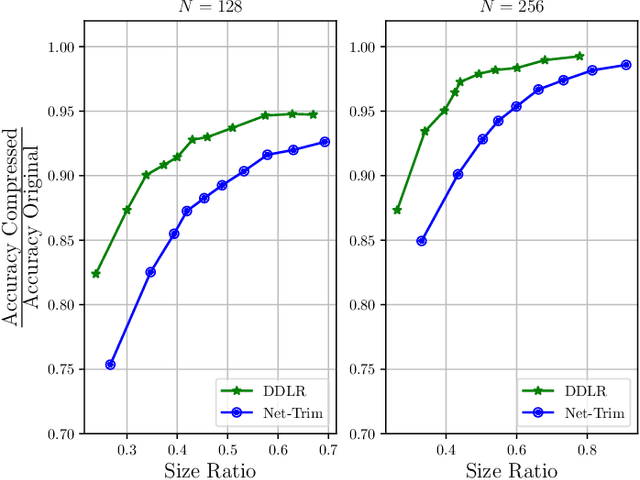
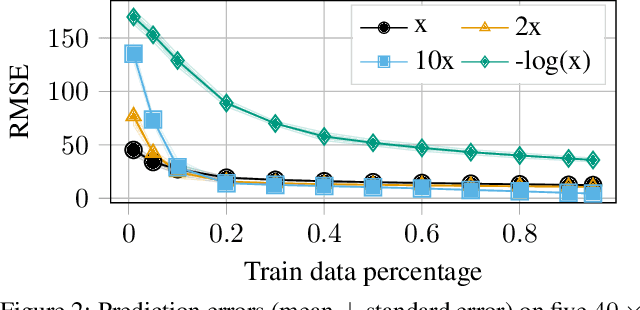
Despite many modern applications of Deep Neural Networks (DNNs), the large number of parameters in the hidden layers makes them unattractive for deployment on devices with storage capacity constraints. In this paper we propose a Data-Driven Low-rank (DDLR) method to reduce the number of parameters of pretrained DNNs and expedite inference by imposing low-rank structure on the fully connected layers, while controlling for the overall accuracy and without requiring any retraining. We pose the problem as finding the lowest rank approximation of each fully connected layer with given performance guarantees and relax it to a tractable convex optimization problem. We show that it is possible to significantly reduce the number of parameters in common DNN architectures with only a small reduction in classification accuracy. We compare DDLR with Net-Trim, which is another data-driven DNN compression technique based on sparsity and show that DDLR consistently produces more compressed neural networks while maintaining higher accuracy.

Efficacy of Bayesian Neural Networks in Active Learning

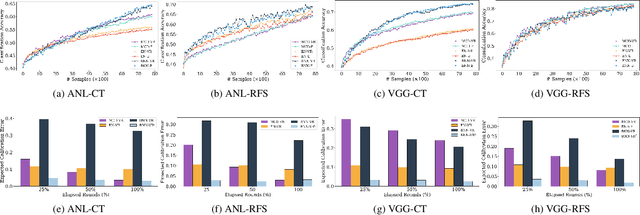
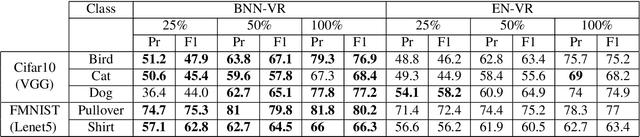
Obtaining labeled data for machine learning tasks can be prohibitively expensive. Active learning mitigates this issue by exploring the unlabeled data space and prioritizing the selection of data that can best improve the model performance. A common approach to active learning is to pick a small sample of data for which the model is most uncertain. In this paper, we explore the efficacy of Bayesian neural networks for active learning, which naturally models uncertainty by learning distribution over the weights of neural networks. By performing a comprehensive set of experiments, we show that Bayesian neural networks are more efficient than ensemble based techniques in capturing uncertainty. Our findings also reveal some key drawbacks of the ensemble techniques, which was recently shown to be more effective than Monte Carlo dropouts.

Matrix Completion in the Unit Hypercube via Structured Matrix Factorization

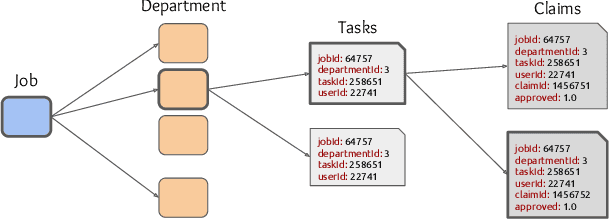
Several complex tasks that arise in organizations can be simplified by mapping them into a matrix completion problem. In this paper, we address a key challenge faced by our company: predicting the efficiency of artists in rendering visual effects (VFX) in film shots. We tackle this challenge by using a two-fold approach: first, we transform this task into a constrained matrix completion problem with entries bounded in the unit interval [0, 1]; second, we propose two novel matrix factorization models that leverage our knowledge of the VFX environment. Our first approach, expertise matrix factorization (EMF), is an interpretable method that structures the latent factors as weighted user-item interplay. The second one, survival matrix factorization (SMF), is instead a probabilistic model for the underlying process defining employees' efficiencies. We show the effectiveness of our proposed models by extensive numerical tests on our VFX dataset and two additional datasets with values that are also bounded in the [0, 1] interval.

Minimum Uncertainty Based Detection of Adversaries in Deep Neural Networks

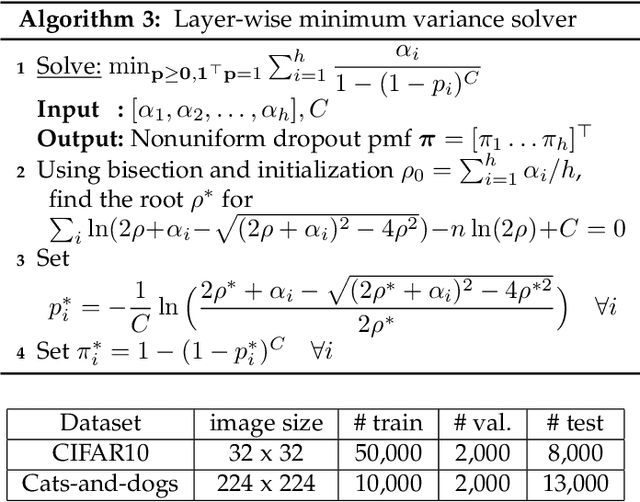
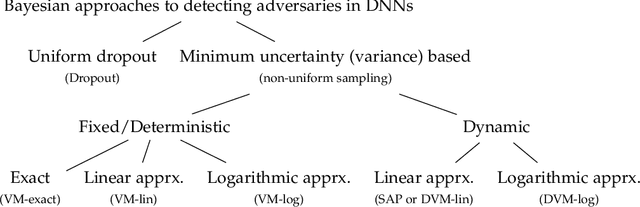
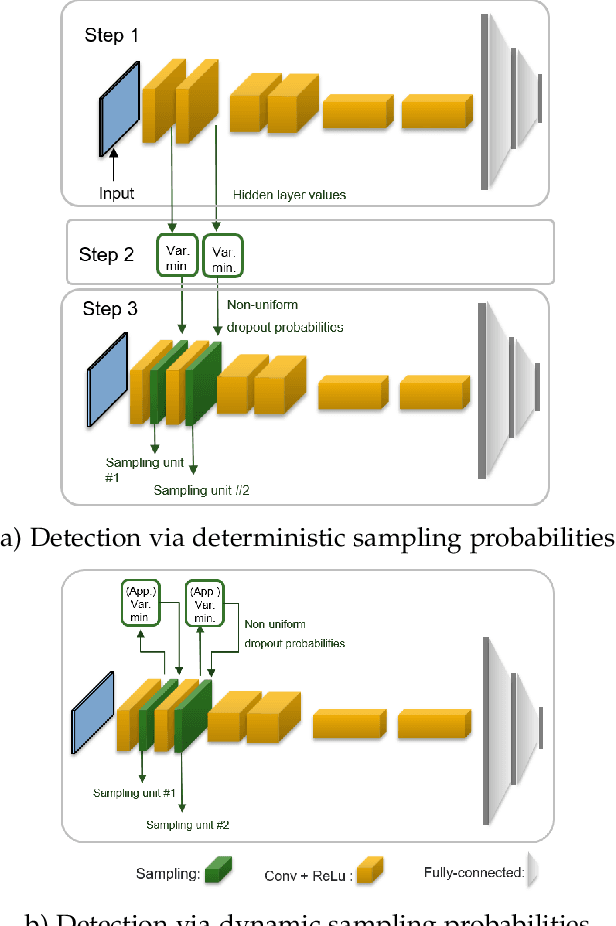
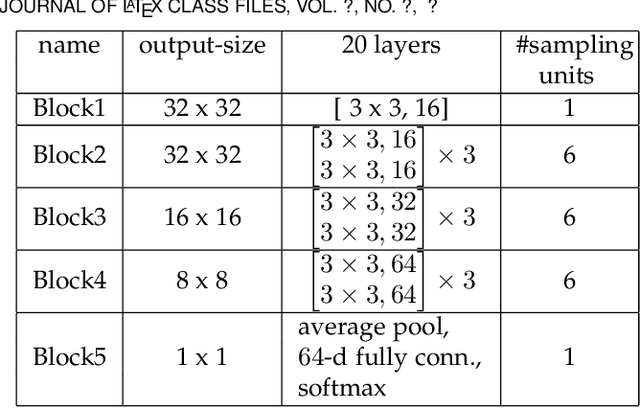
Despite their unprecedented performance in various domains, utilization of Deep Neural Networks (DNNs) in safety-critical environments is severely limited in the presence of even small adversarial perturbations. The present work develops a randomized approach to detecting such perturbations based on minimum uncertainty metrics that rely on sampling at the hidden layers during the DNN inference stage. The sampling probabilities are designed for effective detection of the adversarially corrupted inputs. Being modular, the novel detector of adversaries can be conveniently employed by any pre-trained DNN at no extra training overhead. Selecting which units to sample per hidden layer entails quantifying the amount of DNN output uncertainty from the viewpoint of Bayesian neural networks, where the overall uncertainty is expressed in terms of its layer-wise components - what also promotes scalability. Sampling probabilities are then sought by minimizing uncertainty measures layer-by-layer, leading to a novel convex optimization problem that admits an exact solver with superlinear convergence rate. By simplifying the objective function, low-complexity approximate solvers are also developed. In addition to valuable insights, these approximations link the novel approach with state-of-the-art randomized adversarial detectors. The effectiveness of the novel detectors in the context of competing alternatives is highlighted through extensive tests for various types of adversarial attacks with variable levels of strength.

Learning Generative Models of Structured Signals from Their Superposition Using GANs with Application to Denoising and Demixing

Recently, Generative Adversarial Networks (GANs) have emerged as a popular alternative for modeling complex high dimensional distributions. Most of the existing works implicitly assume that the clean samples from the target distribution are easily available. However, in many applications, this assumption is violated. In this paper, we consider the observation setting when the samples from target distribution are given by the superposition of two structured components and leverage GANs for learning the structure of the components. We propose two novel frameworks: denoising-GAN and demixing-GAN. The denoising-GAN assumes access to clean samples from the second component and try to learn the other distribution, whereas demixing-GAN learns the distribution of the components at the same time. Through extensive numerical experiments, we demonstrate that proposed frameworks can generate clean samples from unknown distributions, and provide competitive performance in tasks such as denoising, demixing, and compressive sensing.

Block CUR: Decomposing Matrices using Groups of Columns

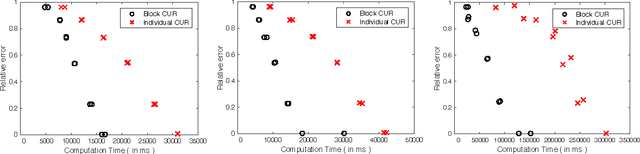
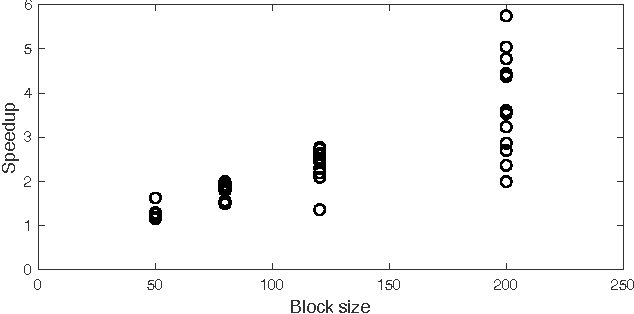
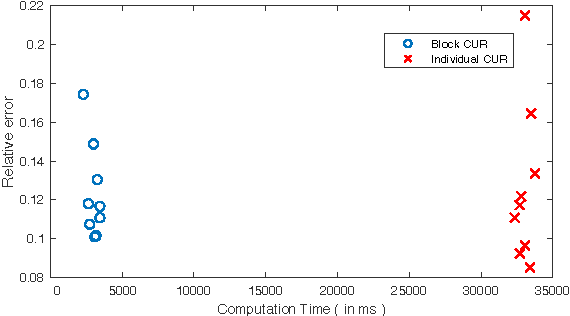
A common problem in large-scale data analysis is to approximate a matrix using a combination of specifically sampled rows and columns, known as CUR decomposition. Unfortunately, in many real-world environments, the ability to sample specific individual rows or columns of the matrix is limited by either system constraints or cost. In this paper, we consider matrix approximation by sampling predefined \emph{blocks} of columns (or rows) from the matrix. We present an algorithm for sampling useful column blocks and provide novel guarantees for the quality of the approximation. This algorithm has application in problems as diverse as biometric data analysis to distributed computing. We demonstrate the effectiveness of the proposed algorithms for computing the Block CUR decomposition of large matrices in a distributed setting with multiple nodes in a compute cluster, where such blocks correspond to columns (or rows) of the matrix stored on the same node, which can be retrieved with much less overhead than retrieving individual columns stored across different nodes. In the biometric setting, the rows correspond to different users and columns correspond to users' biometric reaction to external stimuli, {\em e.g.,}~watching video content, at a particular time instant. There is significant cost in acquiring each user's reaction to lengthy content so we sample a few important scenes to approximate the biometric response. An individual time sample in this use case cannot be queried in isolation due to the lack of context that caused that biometric reaction. Instead, collections of time segments ({\em i.e.,} blocks) must be presented to the user. The practical application of these algorithms is shown via experimental results using real-world user biometric data from a content testing environment.

Improved Support Recovery Guarantees for the Group Lasso With Applications to Structural Health Monitoring

This paper considers the problem of estimating an unknown high dimensional signal from noisy linear measurements, {when} the signal is assumed to possess a \emph{group-sparse} structure in a {known,} fixed dictionary. We consider signals generated according to a natural probabilistic model, and establish new conditions under which the set of indices of the non-zero groups of the signal (called the group-level support) may be accurately estimated via the group Lasso. Our results strengthen existing coherence-based analyses that exhibit the well-known "square root" bottleneck, allowing for the number of recoverable nonzero groups to be nearly as large as the total number of groups. We also establish a sufficient recovery condition relating the number of nonzero groups and the signal to noise ratio (quantified in terms of the ratio of the squared Euclidean norms of nonzero groups and the variance of the random additive {measurement} noise), and validate this trend empirically. Finally, we examine the implications of our results in the context of a structural health monitoring application, where the group Lasso approach facilitates demixing of a propagating acoustic wavefield, acquired on the material surface by a scanning laser Doppler vibrometer, into antithetical components, one of which indicates the locations of internal material defects.