Minimum Uncertainty Based Detection of Adversaries in Deep Neural Networks

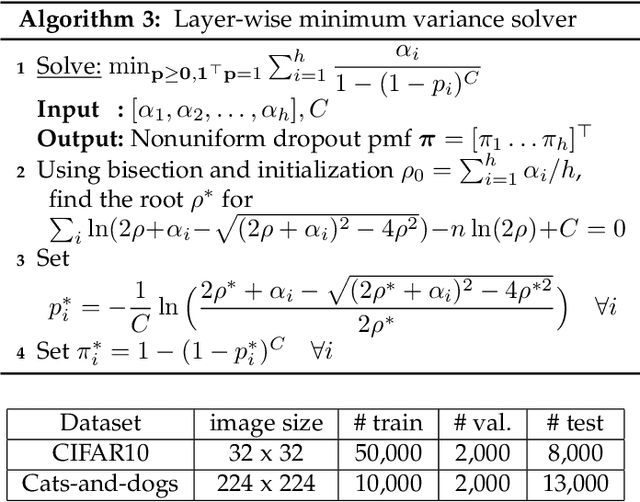
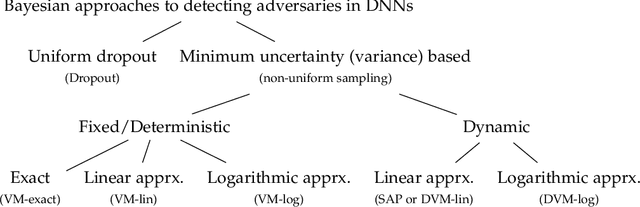
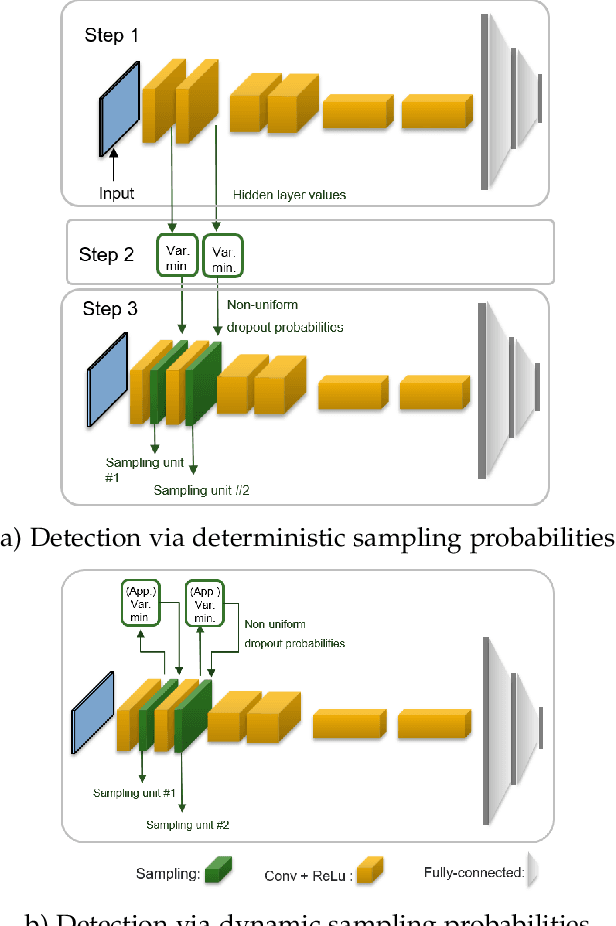
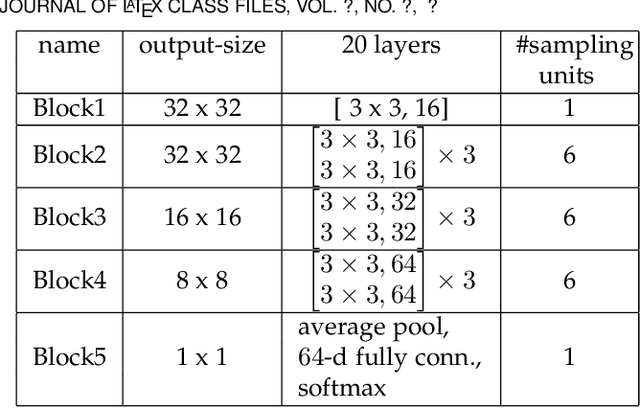
Despite their unprecedented performance in various domains, utilization of Deep Neural Networks (DNNs) in safety-critical environments is severely limited in the presence of even small adversarial perturbations. The present work develops a randomized approach to detecting such perturbations based on minimum uncertainty metrics that rely on sampling at the hidden layers during the DNN inference stage. The sampling probabilities are designed for effective detection of the adversarially corrupted inputs. Being modular, the novel detector of adversaries can be conveniently employed by any pre-trained DNN at no extra training overhead. Selecting which units to sample per hidden layer entails quantifying the amount of DNN output uncertainty from the viewpoint of Bayesian neural networks, where the overall uncertainty is expressed in terms of its layer-wise components - what also promotes scalability. Sampling probabilities are then sought by minimizing uncertainty measures layer-by-layer, leading to a novel convex optimization problem that admits an exact solver with superlinear convergence rate. By simplifying the objective function, low-complexity approximate solvers are also developed. In addition to valuable insights, these approximations link the novel approach with state-of-the-art randomized adversarial detectors. The effectiveness of the novel detectors in the context of competing alternatives is highlighted through extensive tests for various types of adversarial attacks with variable levels of strength.