Solving Reach-Avoid-Stay Problems Using Deep Deterministic Policy Gradients

Reach-Avoid-Stay (RAS) optimal control enables systems such as robots and air taxis to reach their targets, avoid obstacles, and stay near the target. However, current methods for RAS often struggle with handling complex, dynamic environments and scaling to high-dimensional systems. While reinforcement learning (RL)-based reachability analysis addresses these challenges, it has yet to tackle the RAS problem. In this paper, we propose a two-step deep deterministic policy gradient (DDPG) method to extend RL-based reachability method to solve RAS problems. First, we train a function that characterizes the maximal robust control invariant set within the target set, where the system can safely stay, along with its corresponding policy. Second, we train a function that defines the set of states capable of safely reaching the robust control invariant set, along with its corresponding policy. We prove that this method results in the maximal robust RAS set in the absence of training errors and demonstrate that it enables RAS in complex environments, scales to high-dimensional systems, and achieves higher success rates for the RAS task compared to previous methods, validated through one simulation and two high-dimensional experiments.

Interaction-Aware Trajectory Planning for Autonomous Vehicles with Analytic Integration of Neural Networks into Model Predictive Control

Autonomous vehicles (AVs) must share the driving space with other drivers and often employ conservative motion planning strategies to ensure safety. These conservative strategies can negatively impact AV's performance and significantly slow traffic throughput. Therefore, to avoid conservatism, we design an interaction-aware motion planner for the ego vehicle (AV) that interacts with surrounding vehicles to perform complex maneuvers in a locally optimal manner. Our planner uses a neural network-based interactive trajectory predictor and analytically integrates it with model predictive control (MPC). We solve the MPC optimization using the alternating direction method of multipliers (ADMM) and prove the algorithm's convergence. We provide an empirical study and compare our method with a baseline heuristic method.

RAMP: A Risk-Aware Mapping and Planning Pipeline for Fast Off-Road Ground Robot Navigation

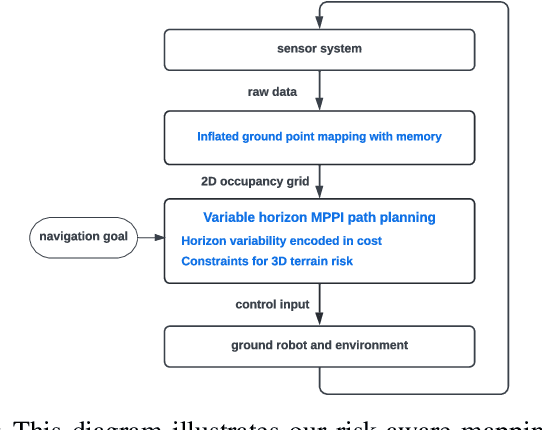
A key challenge in fast ground robot navigation in 3D terrain is balancing robot speed and safety. Recent work has shown that 2.5D maps (2D representations with additional 3D information) are ideal for real-time safe and fast planning. However, raytracing as a prevalent method of generating occupancy grid as the base 2D representation makes the generated map unsafe to plan in, due to inaccurate representation of unknown space. Additionally, existing planners such as MPPI do not reason about speeds in known free and unknown space separately, leading to slow plans. This work therefore first presents ground point inflation as a way to generate accurate occupancy grid maps from classified pointclouds. Then we present an MPPI-based planner with embedded variability in horizon, to maximize speed in known free space while retaining cautionary penetration into unknown space. Finally, we integrate this mapping and planning pipeline with risk constraints arising from 3D terrain, and verify that it enables fast and safe navigation using simulations and a hardware demonstration.

Infinite-Horizon Reach-Avoid Zero-Sum Games via Deep Reinforcement Learning

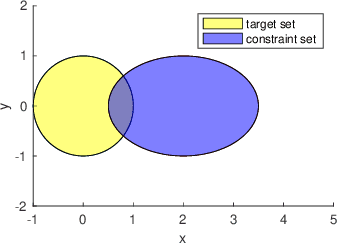
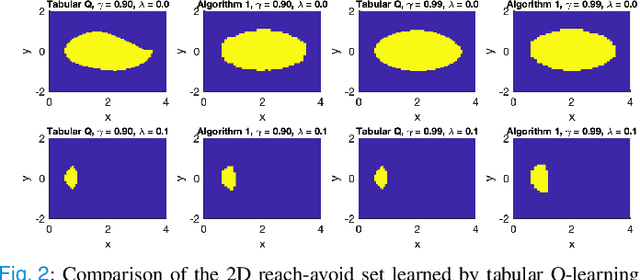
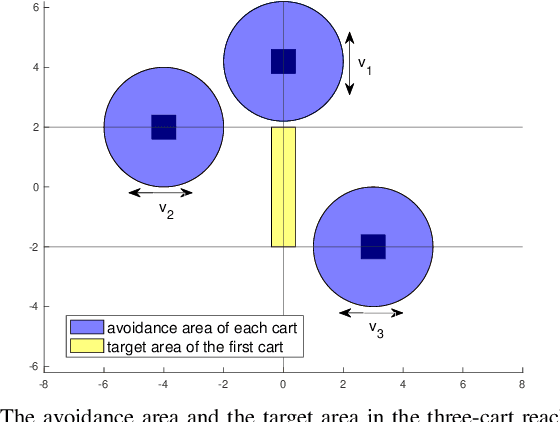
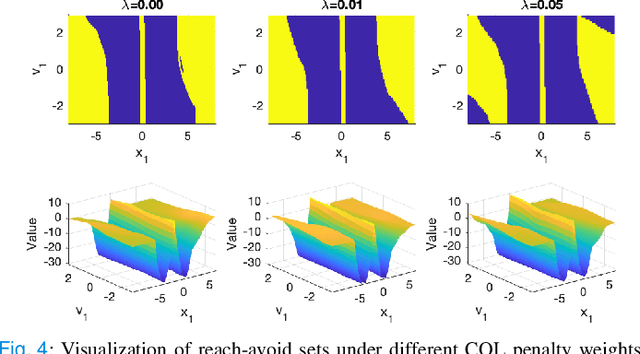
In this paper, we consider the infinite-horizon reach-avoid zero-sum game problem, where the goal is to find a set in the state space, referred to as the reach-avoid set, such that the system starting at a state therein could be controlled to reach a given target set without violating constraints under the worst-case disturbance. We address this problem by designing a new value function with a contracting Bellman backup, where the super-zero level set, i.e., the set of states where the value function is evaluated to be non-negative, recovers the reach-avoid set. Building upon this, we prove that the proposed method can be adapted to compute the viability kernel, or the set of states which could be controlled to satisfy given constraints, and the backward reachable set, or the set of states that could be driven towards a given target set. Finally, we propose to alleviate the curse of dimensionality issue in high-dimensional problems by extending Conservative Q-Learning, a deep reinforcement learning technique, to learn a value function such that the super-zero level set of the learned value function serves as a (conservative) approximation to the reach-avoid set. Our theoretical and empirical results suggest that the proposed method could learn reliably the reach-avoid set and the optimal control policy even with neural network approximation.

Towards cyber-physical systems robust to communication delays: A differential game approach

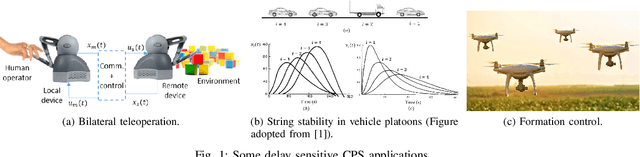
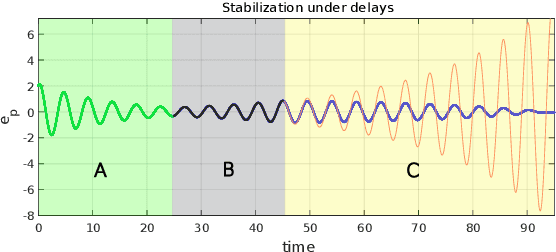
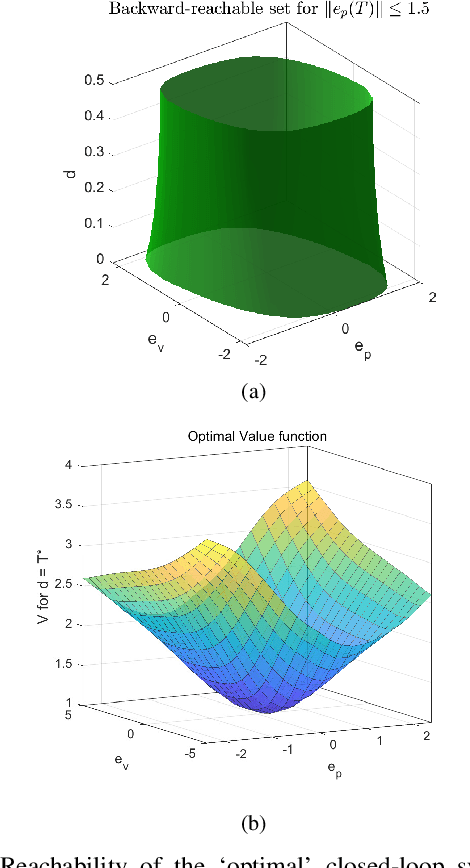
Collaboration between interconnected cyber-physical systems is becoming increasingly pervasive. Time-delays in communication channels between such systems are known to induce catastrophic failure modes, like high frequency oscillations in robotic manipulators in bilateral teleoperation or string instability in platoons of autonomous vehicles. This paper considers nonlinear time-delay systems representing coupled robotic agents, and proposes controllers that are robust to time-varying communication delays. We introduce approximations that allow the delays to be considered as implicit control inputs themselves, and formulate the problem as a zero-sum differential game between the stabilizing controllers and the delays acting adversarially. The ensuing optimal control law is finally compared to known results from Lyapunov-Krasovskii based approaches via numerical experiments.