Robotic Trail Maker Platform for Rehabilitation in Neurological Conditions: Clinical Use Cases

Patients with neurological conditions require rehabilitation to restore their motor, visual, and cognitive abilities. To meet the shortage of therapists and reduce their workload, a robotic rehabilitation platform involving the clinical trail making test is proposed. Therapists can create custom trails for each patient and the patient can trace the trails using a robotic device. The platform can track the performance of the patient and use these data to provide dynamic assistance through the robot to the patient interface. Therefore, the proposed platform not only functions as an evaluation platform, but also trains the patient in recovery. The developed platform has been validated at a rehabilitation center, with therapists and patients operating the device. It was found that patients performed poorly while using the platform compared to healthy subjects and that the assistance provided also improved performance amongst patients. Statistical analysis demonstrated that the speed of the patients was significantly enhanced with the robotic assistance. Further, neural networks are trained to classify between patients and healthy subjects and to forecast their movements using the data collected.

Towards cyber-physical systems robust to communication delays: A differential game approach

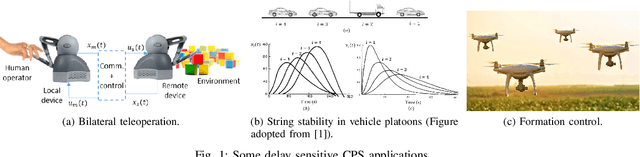
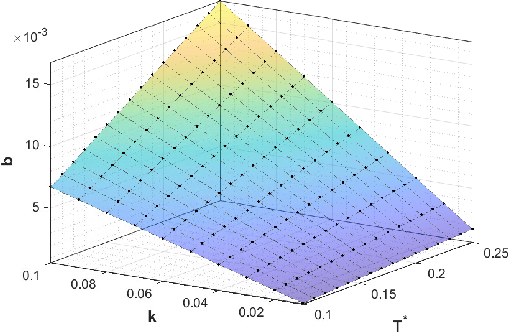
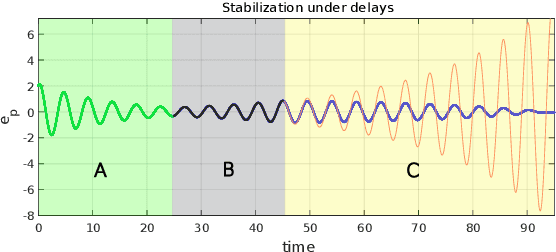
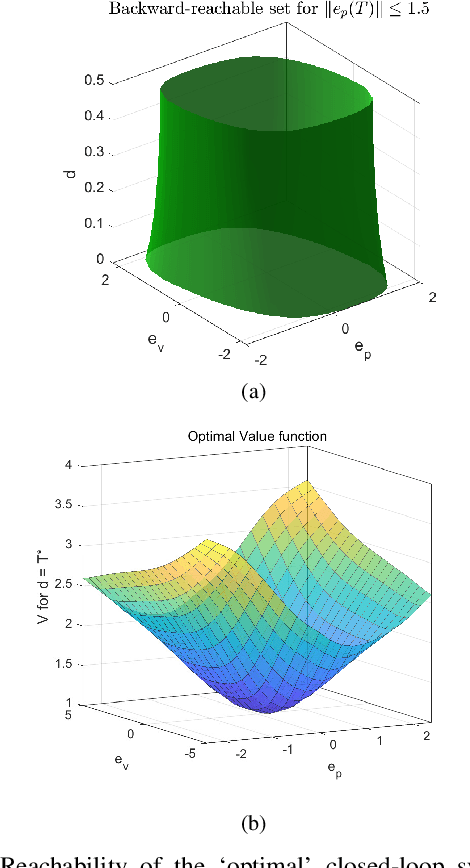
Collaboration between interconnected cyber-physical systems is becoming increasingly pervasive. Time-delays in communication channels between such systems are known to induce catastrophic failure modes, like high frequency oscillations in robotic manipulators in bilateral teleoperation or string instability in platoons of autonomous vehicles. This paper considers nonlinear time-delay systems representing coupled robotic agents, and proposes controllers that are robust to time-varying communication delays. We introduce approximations that allow the delays to be considered as implicit control inputs themselves, and formulate the problem as a zero-sum differential game between the stabilizing controllers and the delays acting adversarially. The ensuing optimal control law is finally compared to known results from Lyapunov-Krasovskii based approaches via numerical experiments.

Dynamically Computing Adversarial Perturbations for Recurrent Neural Networks

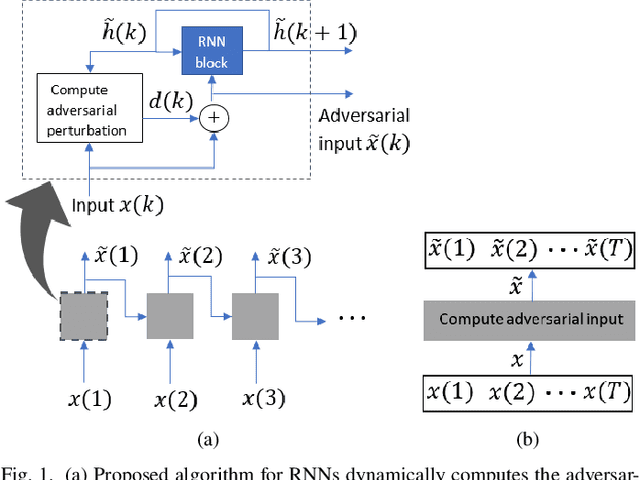
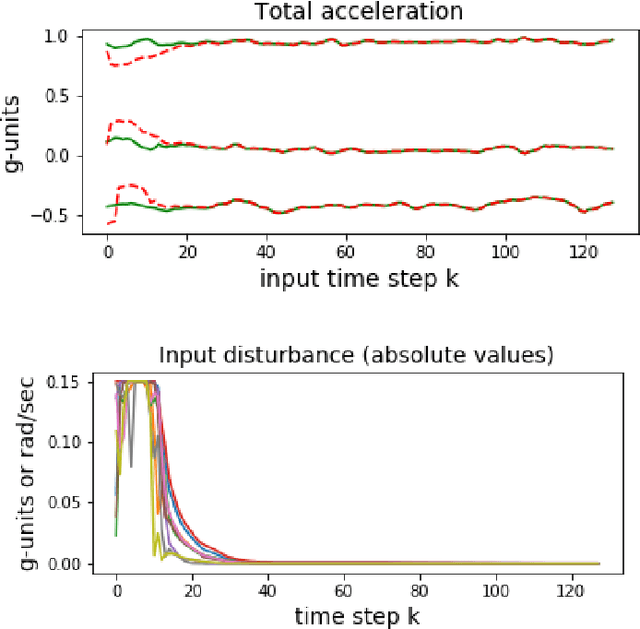
Convolutional and recurrent neural networks have been widely employed to achieve state-of-the-art performance on classification tasks. However, it has also been noted that these networks can be manipulated adversarially with relative ease, by carefully crafted additive perturbations to the input. Though several experimentally established prior works exist on crafting and defending against attacks, it is also desirable to have theoretical guarantees on the existence of adversarial examples and robustness margins of the network to such examples. We provide both in this paper. We focus specifically on recurrent architectures and draw inspiration from dynamical systems theory to naturally cast this as a control problem, allowing us to dynamically compute adversarial perturbations at each timestep of the input sequence, thus resembling a feedback controller. Illustrative examples are provided to supplement the theoretical discussions.