Safety Filters for Black-Box Dynamical Systems by Learning Discriminating Hyperplanes

Learning-based approaches are emerging as an effective approach for safety filters for black-box dynamical systems. Existing methods have relied on certificate functions like Control Barrier Functions (CBFs) and Hamilton-Jacobi (HJ) reachability value functions. The primary motivation for our work is the recognition that ultimately, enforcing the safety constraint as a control input constraint at each state is what matters. By focusing on this constraint, we can eliminate dependence on any specific certificate function-based design. To achieve this, we define a discriminating hyperplane that shapes the half-space constraint on control input at each state, serving as a sufficient condition for safety. This concept not only generalizes over traditional safety methods but also simplifies safety filter design by eliminating dependence on specific certificate functions. We present two strategies to learn the discriminating hyperplane: (a) a supervised learning approach, using pre-verified control invariant sets for labeling, and (b) a reinforcement learning (RL) approach, which does not require such labels. The main advantage of our method, unlike conventional safe RL approaches, is the separation of performance and safety. This offers a reusable safety filter for learning new tasks, avoiding the need to retrain from scratch. As such, we believe that the new notion of the discriminating hyperplane offers a more generalizable direction towards designing safety filters, encompassing and extending existing certificate-function-based or safe RL methodologies.

Constraint-Guided Online Data Selection for Scalable Data-Driven Safety Filters in Uncertain Robotic Systems

As the use of autonomous robotic systems expands in tasks that are complex and challenging to model, the demand for robust data-driven control methods that can certify safety and stability in uncertain conditions is increasing. However, the practical implementation of these methods often faces scalability issues due to the growing amount of data points with system complexity, and a significant reliance on high-quality training data. In response to these challenges, this study presents a scalable data-driven controller that efficiently identifies and infers from the most informative data points for implementing data-driven safety filters. Our approach is grounded in the integration of a model-based certificate function-based method and Gaussian Process (GP) regression, reinforced by a novel online data selection algorithm that reduces time complexity from quadratic to linear relative to dataset size. Empirical evidence, gathered from successful real-world cart-pole swing-up experiments and simulated locomotion of a five-link bipedal robot, demonstrates the efficacy of our approach. Our findings reveal that our efficient online data selection algorithm, which strategically selects key data points, enhances the practicality and efficiency of data-driven certifying filters in complex robotic systems, significantly mitigating scalability concerns inherent in nonparametric learning-based control methods.

Probabilistic Safe Online Learning with Control Barrier Functions

Learning-based control schemes have recently shown great efficacy performing complex tasks. However, in order to deploy them in real systems, it is of vital importance to guarantee that the system will remain safe during online training and execution. We therefore need safe online learning frameworks able to autonomously reason about whether the current information at their disposal is enough to ensure safety or, in contrast, new measurements are required. In this paper, we present a framework consisting of two parts: first, an out-of-distribution detection mechanism actively collecting measurements when needed to guarantee that at least one safety backup direction is always available for use; and second, a Gaussian Process-based probabilistic safety-critical controller that ensures the system stays safe at all times with high probability. Our method exploits model knowledge through the use of Control Barrier Functions, and collects measurements from the stream of online data in an event-triggered fashion to guarantee recursive feasibility of the learned safety-critical controller. This, in turn, allows us to provide formal results of forward invariance of a safe set with high probability, even in a priori unexplored regions. Finally, we validate the proposed framework in numerical simulations of an adaptive cruise control system.

Computation of Regions of Attraction for Hybrid Limit Cycles Using Reachability: An Application to Walking Robots

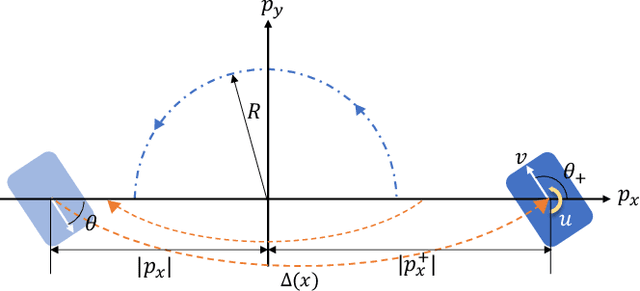
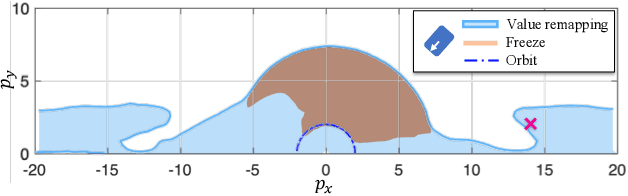
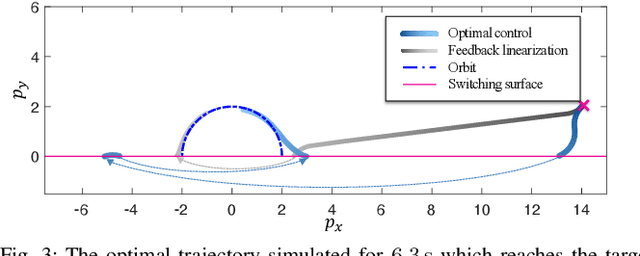
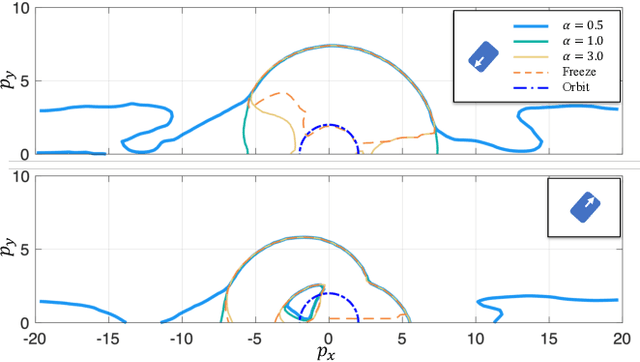
Contact-rich robotic systems, such as legged robots and manipulators, are often represented as hybrid systems. However, the stability analysis and region-of-attraction computation for these systems are often challenging because of the discontinuous state changes upon contact (also referred to as state resets). In this work, we cast the computation of region-ofattraction as a Hamilton-Jacobi (HJ) reachability problem. This enables us to leverage HJ reachability tools that are compatible with general nonlinear system dynamics, and can formally deal with state and input constraints as well as bounded disturbances. Our main contribution is the generalization of HJ reachability framework to account for the discontinuous state changes originating from state resets, which has remained a challenge until now. We apply our approach for computing region-of-attractions for several underactuated walking robots and demonstrate that the proposed approach can (a) recover a bigger region-of-attraction than state-of-the-art approaches, (b) handle state resets, nonlinear dynamics, external disturbances, and input constraints, and (c) also provides a stabilizing controller for the system that can leverage the state resets for enhancing system stability.

Pointwise Feasibility of Gaussian Process-based Safety-Critical Control under Model Uncertainty

Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs) are popular tools for enforcing safety and stability of a controlled system, respectively. They are commonly utilized to build constraints that can be incorporated in a min-norm quadratic program (CBF-CLF-QP) which solves for a safety-critical control input. However, since these constraints rely on a model of the system, when this model is inaccurate the guarantees of safety and stability can be easily lost. In this paper, we present a Gaussian Process (GP)-based approach to tackle the problem of model uncertainty in safety-critical controllers that use CBFs and CLFs. The considered model uncertainty is affected by both state and control input. We derive probabilistic bounds on the effects that such model uncertainty has on the dynamics of the CBF and CLF. Then, we use these bounds to build safety and stability chance constraints that can be incorporated in a min-norm convex optimization program, called GP-CBF-CLF-SOCP. As the main theoretical result of the paper, we present necessary and sufficient conditions for pointwise feasibility of the proposed optimization problem. We believe that these conditions could serve as a starting point towards understanding what are the minimal requirements on the distribution of data collected from the real system in order to guarantee safety. Finally, we validate the proposed framework with numerical simulations of an adaptive cruise controller for an automotive system.

Scalable Learning of Safety Guarantees for Autonomous Systems using Hamilton-Jacobi Reachability

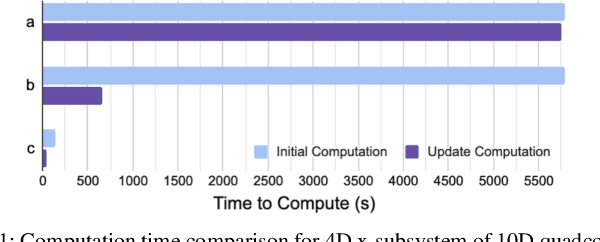
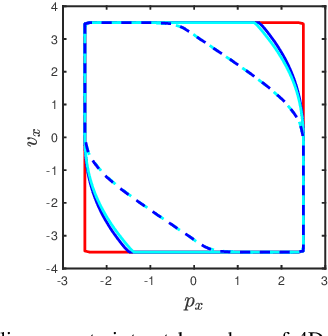
Autonomous systems like aircraft and assistive robots often operate in scenarios where guaranteeing safety is critical. Methods like Hamilton-Jacobi reachability can provide guaranteed safe sets and controllers for such systems. However, often these same scenarios have unknown or uncertain environments, system dynamics, or predictions of other agents. As the system is operating, it may learn new knowledge about these uncertainties and should therefore update its safety analysis accordingly. However, work to learn and update safety analysis is limited to small systems of about two dimensions due to the computational complexity of the analysis. In this paper we synthesize several techniques to speed up computation: decomposition, warm-starting, and adaptive grids. Using this new framework we can update safe sets by one or more orders of magnitude faster than prior work, making this technique practical for many realistic systems. We demonstrate our results on simulated 2D and 10D near-hover quadcopters operating in a windy environment.

Gaussian Process-based Min-norm Stabilizing Controller for Control-Affine Systems with Uncertain Input Effects

This paper presents a method to design a min-norm Control Lyapunov Function (CLF)-based stabilizing controller for a control-affine system with uncertain dynamics using Gaussian Process (GP) regression. We propose a novel compound kernel that captures the control-affine nature of the problem, which permits the estimation of both state and input-dependent model uncertainty in a single GP regression problem. Furthermore, we provide probabilistic guarantees of convergence by the use of GP Upper Confidence Bound analysis and the formulation of a CLF-based stability chance constraint which can be incorporated in a min-norm optimization problem. We show that this resulting optimization problem is convex, and we call it Gaussian Process-based Control Lyapunov Function Second-Order Cone Program (GP-CLF-SOCP). The data-collection process and the training of the GP regression model are carried out in an episodic learning fashion. We validate the proposed algorithm and controller in numerical simulations of an inverted pendulum and a kinematic bicycle model, resulting in stable trajectories which are very similar to the ones obtained if we actually knew the true plant dynamics.