Efficiently Solving Mixed-Hierarchy Games with Quasi-Policy Approximations

Multi-robot coordination often exhibits hierarchical structure, with some robots' decisions depending on the planned behaviors of others. While game theory provides a principled framework for such interactions, existing solvers struggle to handle mixed information structures that combine simultaneous (Nash) and hierarchical (Stackelberg) decision-making. We study N-robot forest-structured mixed-hierarchy games, in which each robot acts as a Stackelberg leader over its subtree while robots in different branches interact via Nash equilibria. We derive the Karush-Kuhn-Tucker (KKT) first-order optimality conditions for this class of games and show that they involve increasingly high-order derivatives of robots' best-response policies as the hierarchy depth grows, rendering a direct solution intractable. To overcome this challenge, we introduce a quasi-policy approximation that removes higher-order policy derivatives and develop an inexact Newton method for efficiently solving the resulting approximated KKT systems. We prove local exponential convergence of the proposed algorithm for games with non-quadratic objectives and nonlinear constraints. The approach is implemented in a highly optimized Julia library (MixedHierarchyGames.jl) and evaluated in simulated experiments, demonstrating real-time convergence for complex mixed-hierarchy information structures.

Generalized Information Gathering Under Dynamics Uncertainty

An agent operating in an unknown dynamical system must learn its dynamics from observations. Active information gathering accelerates this learning, but existing methods derive bespoke costs for specific modeling choices: dynamics models, belief update procedures, observation models, and planners. We present a unifying framework that decouples these choices from the information-gathering cost by explicitly exposing the causal dependencies between parameters, beliefs, and controls. Using this framework, we derive a general information-gathering cost based on Massey's directed information that assumes only Markov dynamics with additive noise and is otherwise agnostic to modeling choices. We prove that the mutual information cost used in existing literature is a special case of our cost. Then, we leverage our framework to establish an explicit connection between the mutual information cost and information gain in linearized Bayesian estimation, thereby providing theoretical justification for mutual information-based active learning approaches. Finally, we illustrate the practical utility of our framework through experiments spanning linear, nonlinear, and multi-agent systems.

TIGER-MARL: Enhancing Multi-Agent Reinforcement Learning with Temporal Information through Graph-based Embeddings and Representations

In this paper, we propose capturing and utilizing \textit{Temporal Information through Graph-based Embeddings and Representations} or \textbf{TIGER} to enhance multi-agent reinforcement learning (MARL). We explicitly model how inter-agent coordination structures evolve over time. While most MARL approaches rely on static or per-step relational graphs, they overlook the temporal evolution of interactions that naturally arise as agents adapt, move, or reorganize cooperation strategies. Capturing such evolving dependencies is key to achieving robust and adaptive coordination. To this end, TIGER constructs dynamic temporal graphs of MARL agents, connecting their current and historical interactions. It then employs a temporal attention-based encoder to aggregate information across these structural and temporal neighborhoods, yielding time-aware agent embeddings that guide cooperative policy learning. Through extensive experiments on two coordination-intensive benchmarks, we show that TIGER consistently outperforms diverse value-decomposition and graph-based MARL baselines in task performance and sample efficiency. Furthermore, we conduct comprehensive ablation studies to isolate the impact of key design parameters in TIGER, revealing how structural and temporal factors can jointly shape effective policy learning in MARL. All codes can be found here: https://github.com/Nikunj-Gupta/tiger-marl.

Value of Information-based Deceptive Path Planning Under Adversarial Interventions

Existing methods for deceptive path planning (DPP) address the problem of designing paths that conceal their true goal from a passive, external observer. Such methods do not apply to problems where the observer has the ability to perform adversarial interventions to impede the path planning agent. In this paper, we propose a novel Markov decision process (MDP)-based model for the DPP problem under adversarial interventions and develop new value of information (VoI) objectives to guide the design of DPP policies. Using the VoI objectives we propose, path planning agents deceive the adversarial observer into choosing suboptimal interventions by selecting trajectories that are of low informational value to the observer. Leveraging connections to the linear programming theory for MDPs, we derive computationally efficient solution methods for synthesizing policies for performing DPP under adversarial interventions. In our experiments, we illustrate the effectiveness of the proposed solution method in achieving deceptiveness under adversarial interventions and demonstrate the superior performance of our approach to both existing DPP methods and conservative path planning approaches on illustrative gridworld problems.

Policies with Sparse Inter-Agent Dependencies in Dynamic Games: A Dynamic Programming Approach

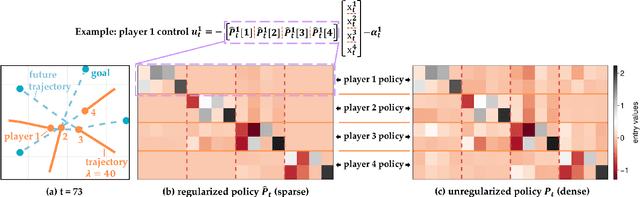
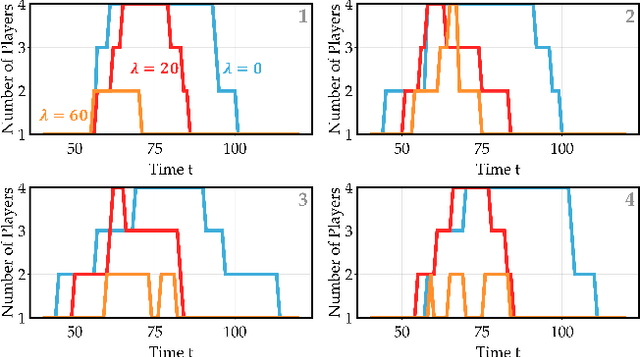
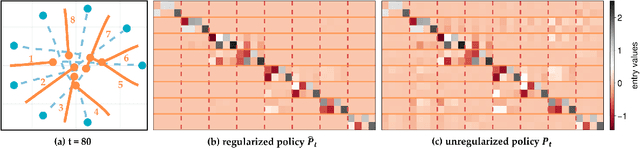
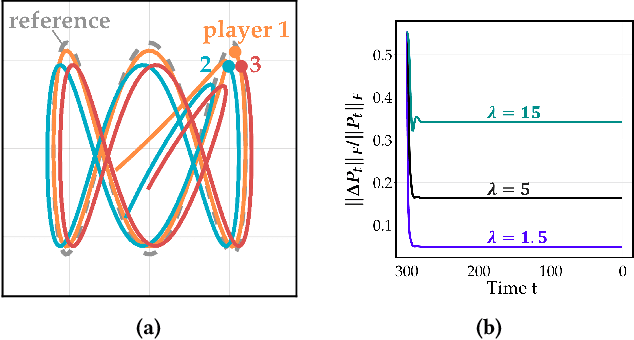
Common feedback strategies in multi-agent dynamic games require all players' state information to compute control strategies. However, in real-world scenarios, sensing and communication limitations between agents make full state feedback expensive or impractical, and such strategies can become fragile when state information from other agents is inaccurate. To this end, we propose a regularized dynamic programming approach for finding sparse feedback policies that selectively depend on the states of a subset of agents in dynamic games. The proposed approach solves convex adaptive group Lasso problems to compute sparse policies approximating Nash equilibrium solutions. We prove the regularized solutions' asymptotic convergence to a neighborhood of Nash equilibrium policies in linear-quadratic (LQ) games. We extend the proposed approach to general non-LQ games via an iterative algorithm. Empirical results in multi-robot interaction scenarios show that the proposed approach effectively computes feedback policies with varying sparsity levels. When agents have noisy observations of other agents' states, simulation results indicate that the proposed regularized policies consistently achieve lower costs than standard Nash equilibrium policies by up to 77% for all interacting agents whose costs are coupled with other agents' states.

Measuring Multi-Source Redundancy in Factor Graphs

Factor graphs are a ubiquitous tool for multi-source inference in robotics and multi-sensor networks. They allow for heterogeneous measurements from many sources to be concurrently represented as factors in the state posterior distribution, so that inference can be conducted via sparse graphical methods. Adding measurements from many sources can supply robustness to state estimation, as seen in distributed pose graph optimization. However, adding excessive measurements to a factor graph can also quickly degrade their performance as more cycles are added to the graph. In both situations, the relevant quality is the redundancy of information. Drawing on recent work in information theory on partial information decomposition (PID), we articulate two potential definitions of redundancy in factor graphs, both within a common axiomatic framework for redundancy in factor graphs. This is the first application of PID to factor graphs, and only one of a few presenting quantitative measures of redundancy for them.