Real-Time Privacy Preservation for Robot Visual Perception

Many robots (e.g., iRobot's Roomba) operate based on visual observations from live video streams, and such observations may inadvertently include privacy-sensitive objects, such as personal identifiers. Existing approaches for preserving privacy rely on deep learning models, differential privacy, or cryptography. They lack guarantees for the complete concealment of all sensitive objects. Guaranteeing concealment requires post-processing techniques and thus is inadequate for real-time video streams. We develop a method for privacy-constrained video streaming, PCVS, that conceals sensitive objects within real-time video streams. PCVS takes a logical specification constraining the existence of privacy-sensitive objects, e.g., never show faces when a person exists. It uses a detection model to evaluate the existence of these objects in each incoming frame. Then, it blurs out a subset of objects such that the existence of the remaining objects satisfies the specification. We then propose a conformal prediction approach to (i) establish a theoretical lower bound on the probability of the existence of these objects in a sequence of frames satisfying the specification and (ii) update the bound with the arrival of each subsequent frame. Quantitative evaluations show that PCVS achieves over 95 percent specification satisfaction rate in multiple datasets, significantly outperforming other methods. The satisfaction rate is consistently above the theoretical bounds across all datasets, indicating that the established bounds hold. Additionally, we deploy PCVS on robots in real-time operation and show that the robots operate normally without being compromised when PCVS conceals objects.

Multi-Fidelity Policy Gradient Algorithms

Many reinforcement learning (RL) algorithms require large amounts of data, prohibiting their use in applications where frequent interactions with operational systems are infeasible, or high-fidelity simulations are expensive or unavailable. Meanwhile, low-fidelity simulators--such as reduced-order models, heuristic reward functions, or generative world models--can cheaply provide useful data for RL training, even if they are too coarse for direct sim-to-real transfer. We propose multi-fidelity policy gradients (MFPGs), an RL framework that mixes a small amount of data from the target environment with a large volume of low-fidelity simulation data to form unbiased, reduced-variance estimators (control variates) for on-policy policy gradients. We instantiate the framework by developing multi-fidelity variants of two policy gradient algorithms: REINFORCE and proximal policy optimization. Experimental results across a suite of simulated robotics benchmark problems demonstrate that when target-environment samples are limited, MFPG achieves up to 3.9x higher reward and improves training stability when compared to baselines that only use high-fidelity data. Moreover, even when the baselines are given more high-fidelity samples--up to 10x as many interactions with the target environment--MFPG continues to match or outperform them. Finally, we observe that MFPG is capable of training effective policies even when the low-fidelity environment is drastically different from the target environment. MFPG thus not only offers a novel paradigm for efficient sim-to-real transfer but also provides a principled approach to managing the trade-off between policy performance and data collection costs.

Inferring Short-Sightedness in Dynamic Noncooperative Games

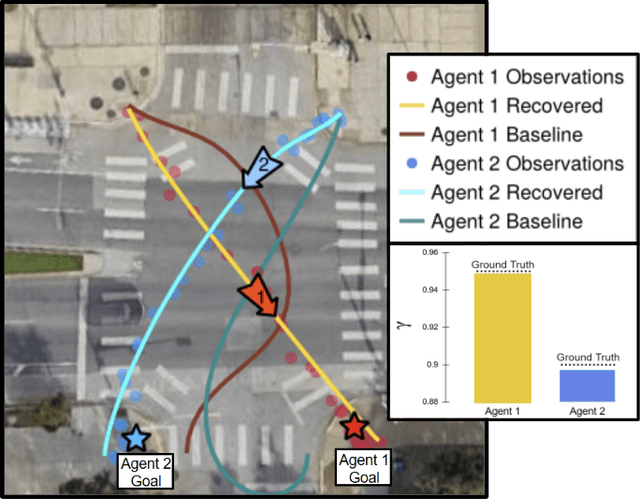
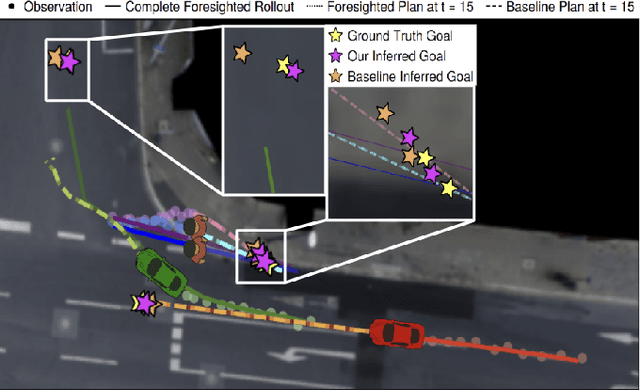
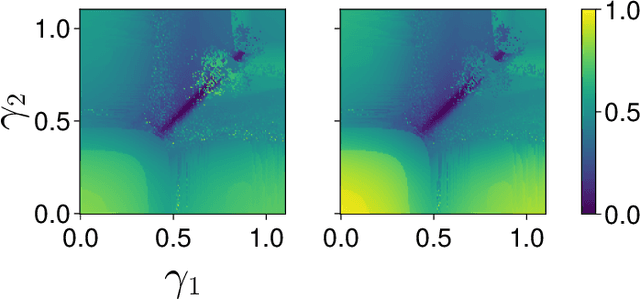
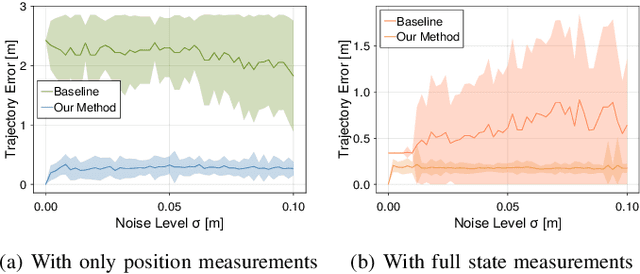
Dynamic game theory is an increasingly popular tool for modeling multi-agent, e.g. human-robot, interactions. Game-theoretic models presume that each agent wishes to minimize a private cost function that depends on others' actions. These games typically evolve over a fixed time horizon, which specifies the degree to which all agents care about the distant future. In practical settings, however, decision-makers may vary in their degree of short-sightedness. We conjecture that quantifying and estimating each agent's short-sightedness from online data will enable safer and more efficient interactions with other agents. To this end, we frame this inference problem as an inverse dynamic game. We consider a specific parametrization of each agent's objective function that smoothly interpolates myopic and farsighted planning. Games of this form are readily transformed into parametric mixed complementarity problems; we exploit the directional differentiability of solutions to these problems with respect to their hidden parameters in order to solve for agents' short-sightedness. We conduct several experiments simulating human behavior at a real-world crosswalk. The results of these experiments clearly demonstrate that by explicitly inferring agents' short-sightedness, we can recover more accurate game-theoretic models, which ultimately allow us to make better predictions of agents' behavior. Specifically, our results show up to a 30% more accurate prediction of myopic behavior compared to the baseline.