Constructive Safety-Critical Control: Synthesizing Control Barrier Functions for Partially Feedback Linearizable Systems

Certifying the safety of nonlinear systems, through the lens of set invariance and control barrier functions (CBFs), offers a powerful method for controller synthesis, provided a CBF can be constructed. This paper draws connections between partial feedback linearization and CBF synthesis. We illustrate that when a control affine system is input-output linearizable with respect to a smooth output function, then, under mild regularity conditions, one may extend any safety constraint defined on the output to a CBF for the full-order dynamics. These more general results are specialized to robotic systems where the conditions required to synthesize CBFs simplify. The CBFs constructed from our approach are applied and verified in simulation and hardware experiments on a quadrotor.

A Constructive Method for Designing Safe Multirate Controllers for Differentially-Flat Systems

We present a multi-rate control architecture that leverages fundamental properties of differential flatness to synthesize controllers for safety-critical nonlinear dynamical systems. We propose a two-layer architecture, where the high-level generates reference trajectories using a linear Model Predictive Controller, and the low-level tracks this reference using a feedback controller. The novelty lies in how we couple these layers, to achieve formal guarantees on recursive feasibility of the MPC problem, and safety of the nonlinear system. Furthermore, using differential flatness, we provide a constructive means to synthesize the multi-rate controller, thereby removing the need to search for suitable Lyapunov or barrier functions, or to approximately linearize/discretize nonlinear dynamics. We show the synthesized controller is a convex optimization problem, making it amenable to real-time implementations. The method is demonstrated experimentally on a ground rover and a quadruped robotic system.

Input-to-State Stability in Probability

Input-to-State Stability (ISS) is fundamental in mathematically quantifying how stability degrades in the presence of bounded disturbances. If a system is ISS, its trajectories will remain bounded, and will converge to a neighborhood of an equilibrium of the undisturbed system. This graceful degradation of stability in the presence of disturbances describes a variety of real-world control implementations. Despite its utility, this property requires the disturbance to be bounded and provides invariance and stability guarantees only with respect to this worst-case bound. In this work, we introduce the concept of ``ISS in probability (ISSp)'' which generalizes ISS to discrete-time systems subject to unbounded stochastic disturbances. Using tools from martingale theory, we provide Lyapunov conditions for a system to be exponentially ISSp, and connect ISSp to stochastic stability conditions found in literature. We exemplify the utility of this method through its application to a bipedal robot confronted with step heights sampled from a truncated Gaussian distribution.

Learning Responsibility Allocations for Safe Human-Robot Interaction with Applications to Autonomous Driving

Drivers have a responsibility to exercise reasonable care to avoid collision with other road users. This assumed responsibility allows interacting agents to maintain safety without explicit coordination. Thus to enable safe autonomous vehicle (AV) interactions, AVs must understand what their responsibilities are to maintain safety and how they affect the safety of nearby agents. In this work we seek to understand how responsibility is shared in multi-agent settings where an autonomous agent is interacting with human counterparts. We introduce Responsibility-Aware Control Barrier Functions (RA-CBFs) and present a method to learn responsibility allocations from data. By combining safety-critical control and learning-based techniques, RA-CBFs allow us to account for scene-dependent responsibility allocations and synthesize safe and efficient driving behaviors without making worst-case assumptions that typically result in overly-conservative behaviors. We test our framework using real-world driving data and demonstrate its efficacy as a tool for both safe control and forensic analysis of unsafe driving.

Safety of Sampled-Data Systems with Control Barrier Functions via Approximate Discrete Time Models

Control Barrier Functions (CBFs) have been demonstrated to be a powerful tool for safety-critical controller design for nonlinear systems. Existing design paradigms do not address the gap between theory (controller design with continuous time models) and practice (the discrete time sampled implementation of the resulting controllers); this can lead to poor performance and violations of safety for hardware instantiations. We propose an approach to close this gap by synthesizing sampled-data counterparts to these CBF-based controllers using approximate discrete time models and Sampled-Data Control Barrier Functions (SD-CBFs). Using properties of a system's continuous time model, we establish a relationship between SD-CBFs and a notion of practical safety for sampled-data systems. Furthermore, we construct convex optimization-based controllers that formally endow nonlinear systems with safety guarantees in practice. We demonstrate the efficacy of these controllers in simulation.

Self-Supervised Online Learning for Safety-Critical Control using Stereo Vision

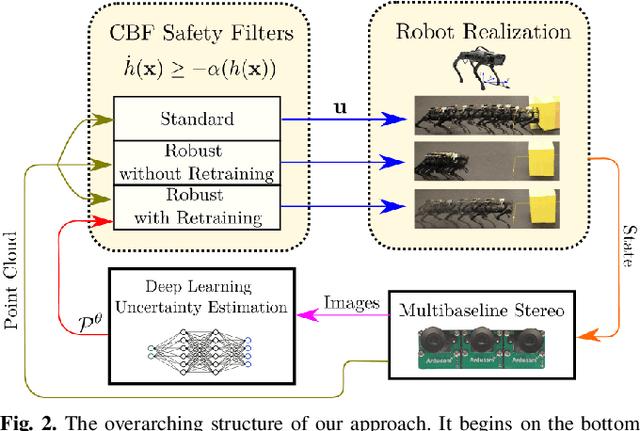
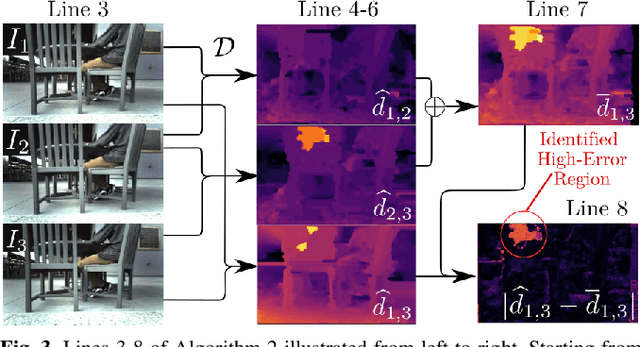
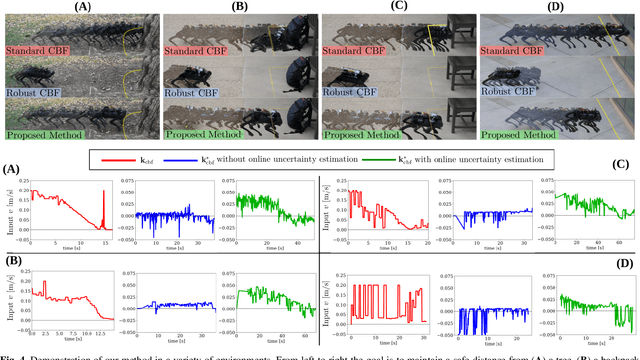
With the increasing prevalence of complex vision-based sensing methods for use in obstacle identification and state estimation, characterizing environment-dependent measurement errors has become a difficult and essential part of modern robotics. This paper presents a self-supervised learning approach to safety-critical control. In particular, the uncertainty associated with stereo vision is estimated, and adapted online to new visual environments, wherein this estimate is leveraged in a safety-critical controller in a robust fashion. To this end, we propose an algorithm that exploits the structure of stereo-vision to learn an uncertainty estimate without the need for ground-truth data. We then robustify existing Control Barrier Function-based controllers to provide safety in the presence of this uncertainty estimate. We demonstrate the efficacy of our method on a quadrupedal robot in a variety of environments. When not using our method safety is violated. With offline training alone we observe the robot is safe, but overly-conservative. With our online method the quadruped remains safe and conservatism is reduced.

Safety-Aware Preference-Based Learning for Safety-Critical Control

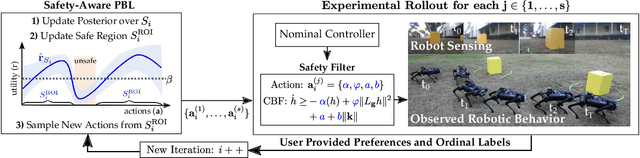
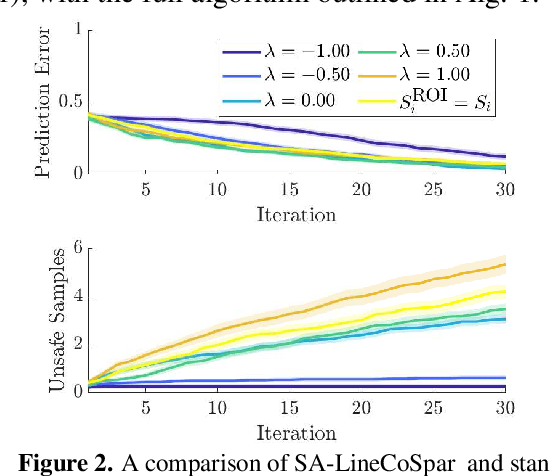
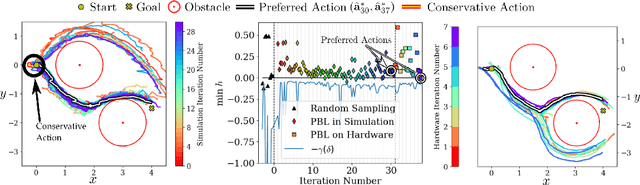
Bringing dynamic robots into the wild requires a tenuous balance between performance and safety. Yet controllers designed to provide robust safety guarantees often result in conservative behavior, and tuning these controllers to find the ideal trade-off between performance and safety typically requires domain expertise or a carefully constructed reward function. This work presents a design paradigm for systematically achieving behaviors that balance performance and robust safety by integrating safety-aware Preference-Based Learning (PBL) with Control Barrier Functions (CBFs). Fusing these concepts -- safety-aware learning and safety-critical control -- gives a robust means to achieve safe behaviors on complex robotic systems in practice. We demonstrate the capability of this design paradigm to achieve safe and performant perception-based autonomous operation of a quadrupedal robot both in simulation and experimentally on hardware.

Model-Free Safety-Critical Control for Robotic Systems

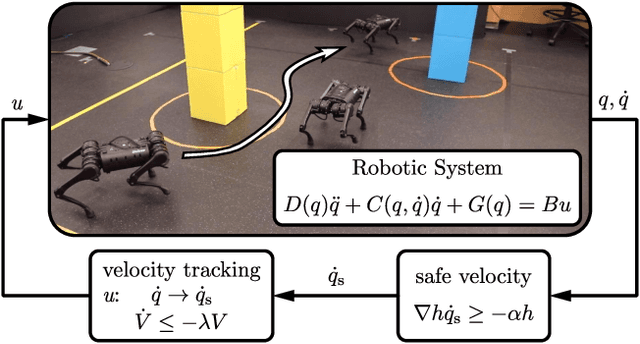
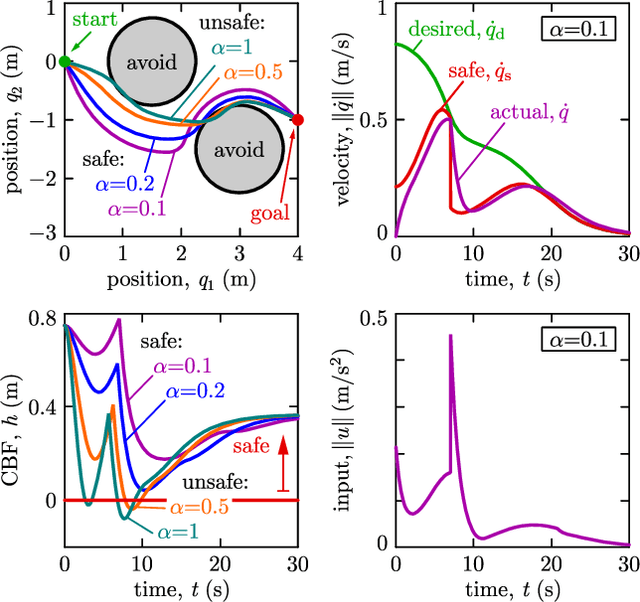
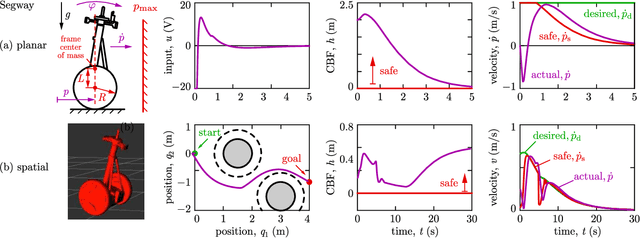
This paper presents a framework for the safety-critical control of robotic systems, when safety is defined on safe regions in the configuration space. To maintain safety, we synthesize a safe velocity based on control barrier function theory without relying on a -- potentially complicated -- high-fidelity dynamical model of the robot. Then, we track the safe velocity with a tracking controller. This culminates in model-free safety critical control. We prove theoretical safety guarantees for the proposed method. Finally, we demonstrate that this approach is application-agnostic. We execute an obstacle avoidance task with a Segway in high-fidelity simulation, as well as with a Drone and a Quadruped in hardware experiments.

Episodic Learning for Safe Bipedal Locomotion with Control Barrier Functions and Projection-to-State Safety

This paper combines episodic learning and control barrier functions in the setting of bipedal locomotion. The safety guarantees that control barrier functions provide are only valid with perfect model knowledge; however, this assumption cannot be met on hardware platforms. To address this, we utilize the notion of projection-to-state safety paired with a machine learning framework in an attempt to learn the model uncertainty as it affects the barrier functions. The proposed approach is demonstrated both in simulation and on hardware for the AMBER-3M bipedal robot in the context of the stepping-stone problem, which requires precise foot placement while walking dynamically.

Guaranteeing Safety of Learned Perception Modules via Measurement-Robust Control Barrier Functions

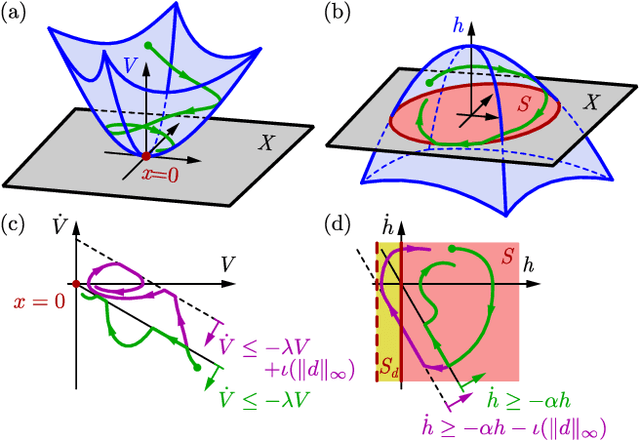
Modern nonlinear control theory seeks to develop feedback controllers that endow systems with properties such as safety and stability. The guarantees ensured by these controllers often rely on accurate estimates of the system state for determining control actions. In practice, measurement model uncertainty can lead to error in state estimates that degrades these guarantees. In this paper, we seek to unify techniques from control theory and machine learning to synthesize controllers that achieve safety in the presence of measurement model uncertainty. We define the notion of a Measurement-Robust Control Barrier Function (MR-CBF) as a tool for determining safe control inputs when facing measurement model uncertainty. Furthermore, MR-CBFs are used to inform sampling methodologies for learning-based perception systems and quantify tolerable error in the resulting learned models. We demonstrate the efficacy of MR-CBFs in achieving safety with measurement model uncertainty on a simulated Segway system.