Safety-Critical Controller Synthesis with Reduced-Order Models

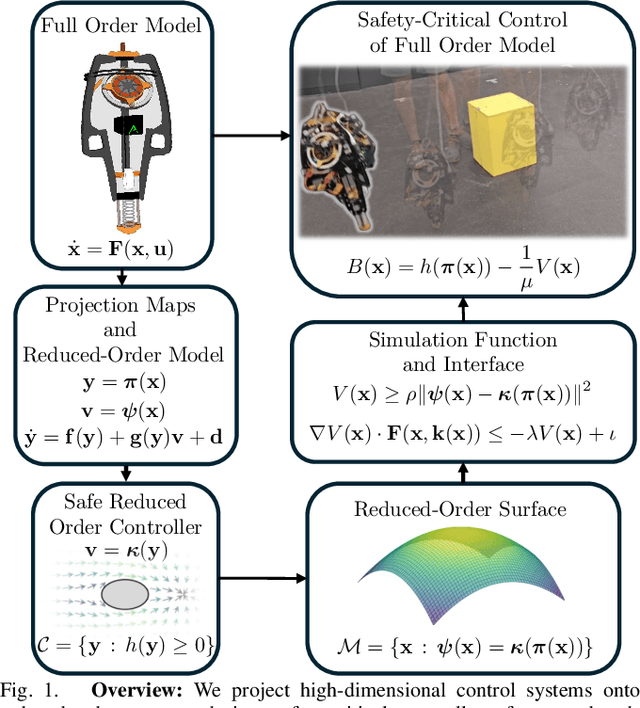
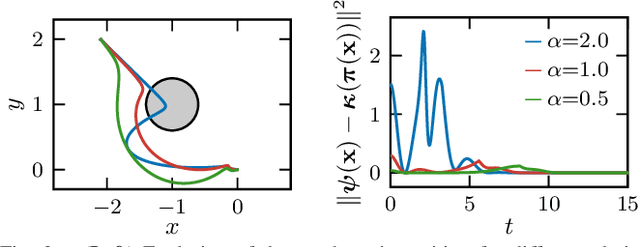
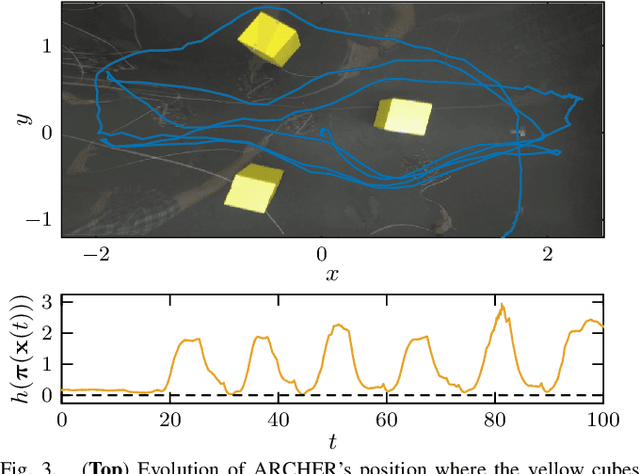
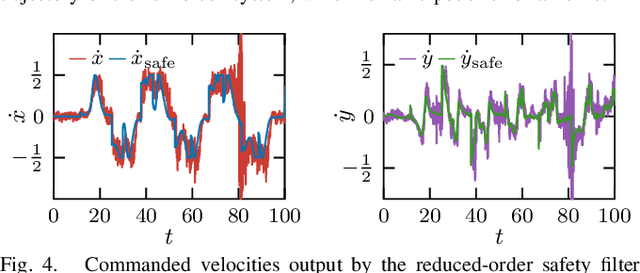
Reduced-order models (ROMs) provide lower dimensional representations of complex systems, capturing their salient features while simplifying control design. Building on previous work, this paper presents an overarching framework for the integration of ROMs and control barrier functions, enabling the use of simplified models to construct safety-critical controllers while providing safety guarantees for complex full-order models. To achieve this, we formalize the connection between full and ROMs by defining projection mappings that relate the states and inputs of these models and leverage simulation functions to establish conditions under which safety guarantees may be transferred from a ROM to its corresponding full-order model. The efficacy of our framework is illustrated through simulation results on a drone and hardware demonstrations on ARCHER, a 3D hopping robot.

Dynamic Tube MPC: Learning Tube Dynamics with Massively Parallel Simulation for Robust Safety in Practice

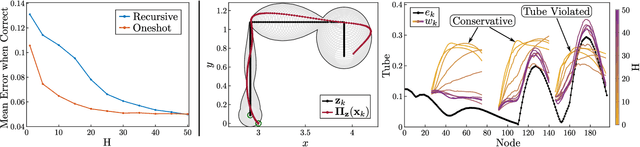
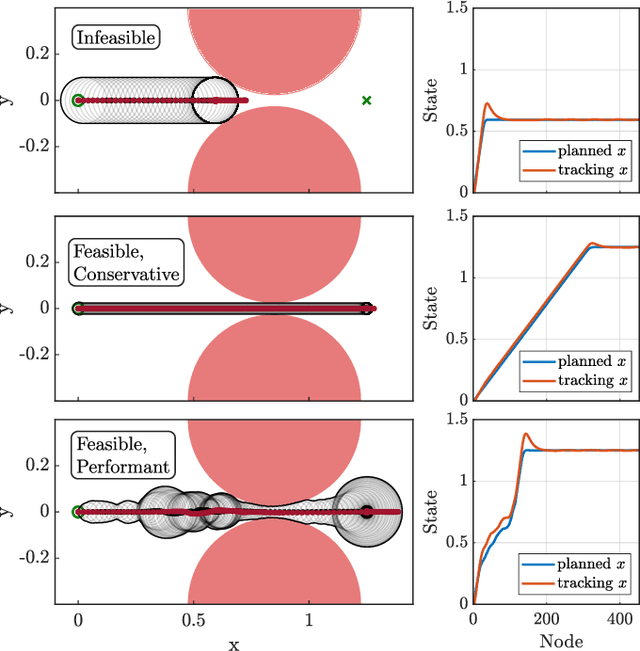
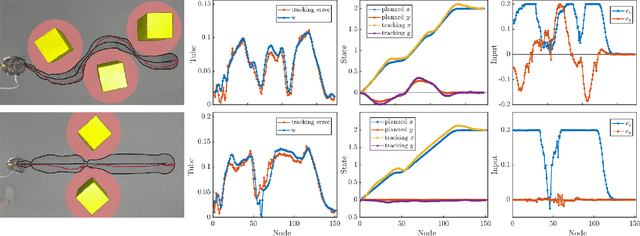
Safe navigation of cluttered environments is a critical challenge in robotics. It is typically approached by separating the planning and tracking problems, with planning executed on a reduced order model to generate reference trajectories, and control techniques used to track these trajectories on the full order dynamics. Inevitable tracking error necessitates robustification of the nominal plan to ensure safety; in many cases, this is accomplished via worst-case bounding, which ignores the fact that some trajectories of the planning model may be easier to track than others. In this work, we present a novel method leveraging massively parallel simulation to learn a dynamic tube representation, which characterizes tracking performance as a function of actions taken by the planning model. Planning model trajectories are then optimized such that the dynamic tube lies in the free space, allowing a balance between performance and safety to be traded off in real time. The resulting Dynamic Tube MPC is applied to the 3D hopping robot ARCHER, enabling agile and performant navigation of cluttered environments, and safe collision-free traversal of narrow corridors.

Bezier Reachable Polytopes: Efficient Certificates for Robust Motion Planning with Layered Architectures

Control architectures are often implemented in a layered fashion, combining independently designed blocks to achieve complex tasks. Providing guarantees for such hierarchical frameworks requires considering the capabilities and limitations of each layer and their interconnections at design time. To address this holistic design challenge, we introduce the notion of Bezier Reachable Polytopes -- certificates of reachable points in the space of Bezier polynomial reference trajectories. This approach captures the set of trajectories that can be tracked by a low-level controller while satisfying state and input constraints, and leverages the geometric properties of Bezier polynomials to maintain an efficient polytopic representation. As a result, these certificates serve as a constructive tool for layered architectures, enabling long-horizon tasks to be reasoned about in a computationally tractable manner.

Dynamically Feasible Path Planning in Cluttered Environments via Reachable Bezier Polytopes

The deployment of robotic systems in real world environments requires the ability to quickly produce paths through cluttered, non-convex spaces. These planned trajectories must be both kinematically feasible (i.e., collision free) and dynamically feasible (i.e., satisfy the underlying system dynamics), necessitating a consideration of both the free space and the dynamics of the robot in the path planning phase. In this work, we explore the application of reachable Bezier polytopes as an efficient tool for generating trajectories satisfying both kinematic and dynamic requirements. Furthermore, we demonstrate that by offloading specific computation tasks to the GPU, such an algorithm can meet tight real time requirements. We propose a layered control architecture that efficiently produces collision free and dynamically feasible paths for nonlinear control systems, and demonstrate the framework on the tasks of 3D hopping in a cluttered environment.

Robust Agility via Learned Zero Dynamics Policies

We study the design of robust and agile controllers for hybrid underactuated systems. Our approach breaks down the task of creating a stabilizing controller into: 1) learning a mapping that is invariant under optimal control, and 2) driving the actuated coordinates to the output of that mapping. This approach, termed Zero Dynamics Policies, exploits the structure of underactuation by restricting the inputs of the target mapping to the subset of degrees of freedom that cannot be directly actuated, thereby achieving significant dimension reduction. Furthermore, we retain the stability and constraint satisfaction of optimal control while reducing the online computational overhead. We prove that controllers of this type stabilize hybrid underactuated systems and experimentally validate our approach on the 3D hopping platform, ARCHER. Over the course of 3000 hops the proposed framework demonstrates robust agility, maintaining stable hopping while rejecting disturbances on rough terrain.

Nonlinear Model Predictive Control of a 3D Hopping Robot: Leveraging Lie Group Integrators for Dynamically Stable Behaviors

Achieving stable hopping has been a hallmark challenge in the field of dynamic legged locomotion. Controlled hopping is notably difficult due to extended periods of underactuation, combined with very short ground phases wherein ground interactions must be modulated to regulate global state. In this work, we explore the use of hybrid nonlinear model predictive control, paired with a low-level feedback controller in a multi-rate hierarchy, to achieve dynamically stable motions on a novel 3D hopping robot. In order to demonstrate richer behaviors on the manifold of rotations, both the planning and feedback layers must be done in a geometrically consistent fashion; therefore, we develop the necessary tools to employ Lie group integrators and an appropriate feedback controller. We experimentally demonstrate stable 3D hopping on a novel robot, as well as trajectory tracking and flipping in simulation.

Robust Bipedal Locomotion: Leveraging Saltation Matrices for Gait Optimization

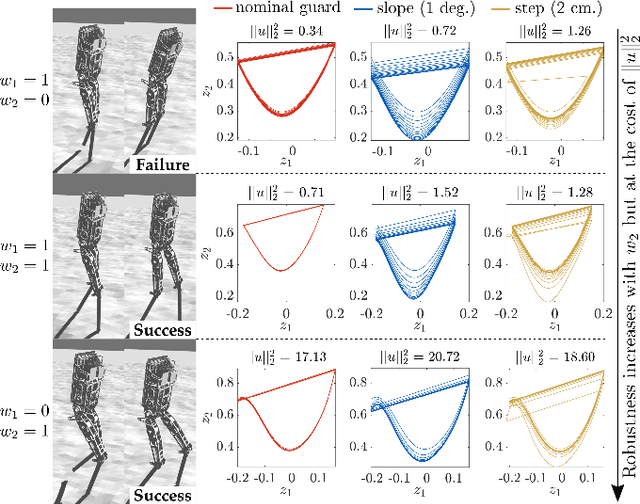
The ability to generate robust walking gaits on bipedal robots is key to their successful realization on hardware. To this end, this work extends the method of Hybrid Zero Dynamics (HZD) -- which traditionally only accounts for locomotive stability via periodicity constraints under perfect impact events -- through the inclusion of the saltation matrix with a view toward synthesizing robust walking gaits. By jointly minimizing the norm of the extended saltation matrix and the torque of the robot directly in the gait generation process, we show that the synthesized gaits are more robust than gaits generated with either term alone; these results are shown in simulation and on hardware for both the AMBER-3M planar biped and the Atalante lower-body exoskeleton (both with and without a human subject). The end result is experimental validation that combining saltation matrices with HZD methods produces more robust bipedal walking in practice.

Neural Gaits: Learning Bipedal Locomotion via Control Barrier Functions and Zero Dynamics Policies

This work presents Neural Gaits, a method for learning dynamic walking gaits through the enforcement of set invariance that can be refined episodically using experimental data from the robot. We frame walking as a set invariance problem enforceable via control barrier functions (CBFs) defined on the reduced-order dynamics quantifying the underactuated component of the robot: the zero dynamics. Our approach contains two learning modules: one for learning a policy that satisfies the CBF condition, and another for learning a residual dynamics model to refine imperfections of the nominal model. Importantly, learning only over the zero dynamics significantly reduces the dimensionality of the learning problem while using CBFs allows us to still make guarantees for the full-order system. The method is demonstrated experimentally on an underactuated bipedal robot, where we are able to show agile and dynamic locomotion, even with partially unknown dynamics.

Bipedal Locomotion with Nonlinear Model Predictive Control: Online Gait Generation using Whole-Body Dynamics

The ability to generate dynamic walking in real-time for bipedal robots with compliance and underactuation has the potential to enable locomotion in complex and unstructured environments. Yet, the high-dimensional nature of bipedal robots has limited the use of full-order rigid body dynamics to gaits which are synthesized offline and then tracked online, e.g., via whole-body controllers. In this work we develop an online nonlinear model predictive control approach that leverages the full-order dynamics to realize diverse walking behaviors. Additionally, this approach can be coupled with gaits synthesized offline via a terminal cost that enables a shorter prediction horizon; this makes rapid online re-planning feasible and bridges the gap between online reactive control and offline gait planning. We demonstrate the proposed method on the planar robot AMBER-3M, both in simulation and on hardware.

Interactive multi-modal motion planning with Branch Model Predictive Control

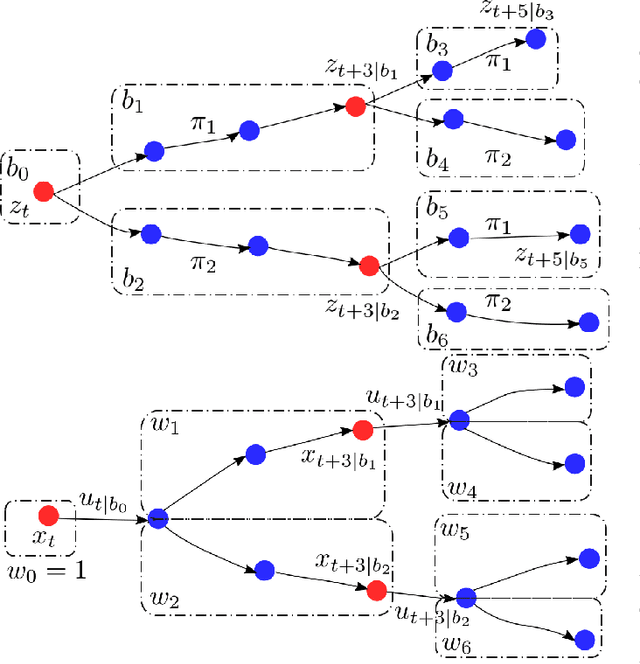
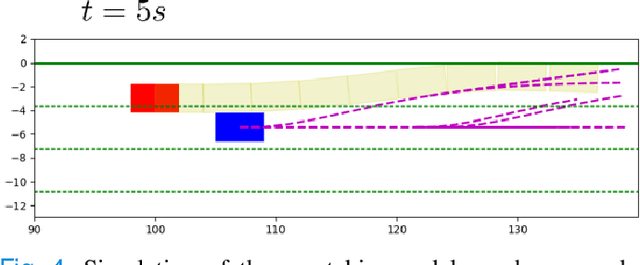
Motion planning for autonomous robots and vehicles in presence of uncontrolled agents remains a challenging problem as the reactive behaviors of the uncontrolled agents must be considered. Since the uncontrolled agents usually demonstrate multimodal reactive behavior, the motion planner needs to solve a continuous motion planning problem under these behaviors, which contains a discrete element. We propose a branch Model Predictive Control (MPC) framework that plans over feedback policies to leverage the reactive behavior of the uncontrolled agent. In particular, a scenario tree is constructed from a finite set of policies of the uncontrolled agent, and the branch MPC solves for a feedback policy in the form of a trajectory tree, which shares the same topology as the scenario tree. Moreover, coherent risk measures such as the Conditional Value at Risk (CVaR) are used as a tuning knob to adjust the tradeoff between performance and robustness. The proposed branch MPC framework is tested on an overtake and lane change task and a merging task for autonomous vehicles in simulation, and on the motion planning of an autonomous quadruped robot alongside an uncontrolled quadruped in experiments. The result demonstrates interesting human-like behaviors, achieving a balance between safety and performance.