Robust Agility via Learned Zero Dynamics Policies

We study the design of robust and agile controllers for hybrid underactuated systems. Our approach breaks down the task of creating a stabilizing controller into: 1) learning a mapping that is invariant under optimal control, and 2) driving the actuated coordinates to the output of that mapping. This approach, termed Zero Dynamics Policies, exploits the structure of underactuation by restricting the inputs of the target mapping to the subset of degrees of freedom that cannot be directly actuated, thereby achieving significant dimension reduction. Furthermore, we retain the stability and constraint satisfaction of optimal control while reducing the online computational overhead. We prove that controllers of this type stabilize hybrid underactuated systems and experimentally validate our approach on the 3D hopping platform, ARCHER. Over the course of 3000 hops the proposed framework demonstrates robust agility, maintaining stable hopping while rejecting disturbances on rough terrain.

FI-ODE: Certified and Robust Forward Invariance in Neural ODEs

We study how to certifiably enforce forward invariance properties in neural ODEs. Forward invariance implies that the hidden states of the ODE will stay in a ``good'' region, and a robust version would hold even under adversarial perturbations to the input. Such properties can be used to certify desirable behaviors such as adversarial robustness (the hidden states stay in the region that generates accurate classification even under input perturbations) and safety in continuous control (the system never leaves some safe set). We develop a general approach using tools from non-linear control theory and sampling-based verification. Our approach empirically produces the strongest adversarial robustness guarantees compared to prior work on certifiably robust ODE-based models (including implicit-depth models).

Safe Drone Flight with Time-Varying Backup Controllers

The weight, space, and power limitations of small aerial vehicles often prevent the application of modern control techniques without significant model simplifications. Moreover, high-speed agile behavior, such as that exhibited in drone racing, make these simplified models too unreliable for safety-critical control. In this work, we introduce the concept of time-varying backup controllers (TBCs): user-specified maneuvers combined with backup controllers that generate reference trajectories which guarantee the safety of nonlinear systems. TBCs reduce conservatism when compared to traditional backup controllers and can be directly applied to multi-agent coordination to guarantee safety. Theoretically, we provide conditions under which TBCs strictly reduce conservatism, describe how to switch between several TBC's and show how to embed TBCs in a multi-agent setting. Experimentally, we verify that TBCs safely increase operational freedom when filtering a pilot's actions and demonstrate robustness and computational efficiency when applied to decentralized safety filtering of two quadrotors.

Neural Gaits: Learning Bipedal Locomotion via Control Barrier Functions and Zero Dynamics Policies

This work presents Neural Gaits, a method for learning dynamic walking gaits through the enforcement of set invariance that can be refined episodically using experimental data from the robot. We frame walking as a set invariance problem enforceable via control barrier functions (CBFs) defined on the reduced-order dynamics quantifying the underactuated component of the robot: the zero dynamics. Our approach contains two learning modules: one for learning a policy that satisfies the CBF condition, and another for learning a residual dynamics model to refine imperfections of the nominal model. Importantly, learning only over the zero dynamics significantly reduces the dimensionality of the learning problem while using CBFs allows us to still make guarantees for the full-order system. The method is demonstrated experimentally on an underactuated bipedal robot, where we are able to show agile and dynamic locomotion, even with partially unknown dynamics.

LyaNet: A Lyapunov Framework for Training Neural ODEs

We propose a method for training ordinary differential equations by using a control-theoretic Lyapunov condition for stability. Our approach, called LyaNet, is based on a novel Lyapunov loss formulation that encourages the inference dynamics to converge quickly to the correct prediction. Theoretically, we show that minimizing Lyapunov loss guarantees exponential convergence to the correct solution and enables a novel robustness guarantee. We also provide practical algorithms, including one that avoids the cost of backpropagating through a solver or using the adjoint method. Relative to standard Neural ODE training, we empirically find that LyaNet can offer improved prediction performance, faster convergence of inference dynamics, and improved adversarial robustness. Our code available at https://github.com/ivandariojr/LyapunovLearning .

Interpretable Reinforcement Learning via Differentiable Decision Trees

Decision trees are ubiquitous in machine learning for their ease of use and interpretability; however, they are not typically implemented in reinforcement learning because they cannot be updated via stochastic gradient descent. Traditional applications of decision trees for reinforcement learning have focused instead on making commitments to decision boundaries as the tree is grown one layer at a time. We overcome this critical limitation by allowing for a gradient update over the entire tree structure that improves sample complexity when a tree is fuzzy and interpretability when sharp. We offer three key contributions towards this goal. First, we motivate the need for policy gradient-based learning by examining the theoretical properties of gradient descent over differentiable decision trees. Second, we introduce a regularization framework that yields interpretability via sparsity in the tree structure. Third, we demonstrate the ability to construct a decision tree via policy gradient in canonical reinforcement learning domains and supervised learning benchmarks.

Differentiable MPC for End-to-end Planning and Control

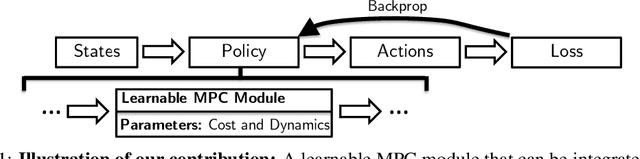
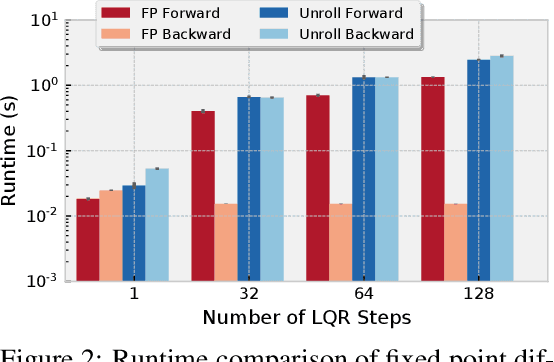
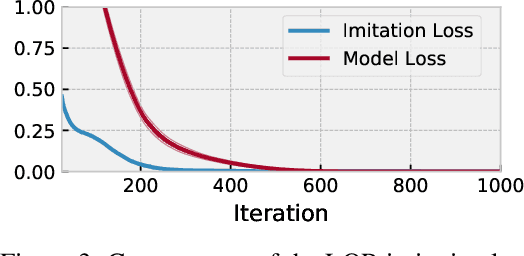
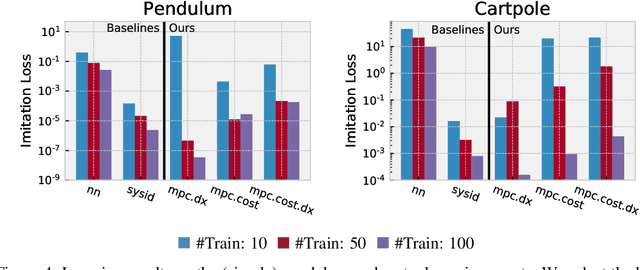
We present foundations for using Model Predictive Control (MPC) as a differentiable policy class for reinforcement learning in continuous state and action spaces. This provides one way of leveraging and combining the advantages of model-free and model-based approaches. Specifically, we differentiate through MPC by using the KKT conditions of the convex approximation at a fixed point of the controller. Using this strategy, we are able to learn the cost and dynamics of a controller via end-to-end learning. Our experiments focus on imitation learning in the pendulum and cartpole domains, where we learn the cost and dynamics terms of an MPC policy class. We show that our MPC policies are significantly more data-efficient than a generic neural network and that our method is superior to traditional system identification in a setting where the expert is unrealizable.