HALO: Hybrid Auto-encoded Locomotion with Learned Latent Dynamics, Poincaré Maps, and Regions of Attraction

Reduced-order models are powerful for analyzing and controlling high-dimensional dynamical systems. Yet constructing these models for complex hybrid systems such as legged robots remains challenging. Classical approaches rely on hand-designed template models (e.g., LIP, SLIP), which, though insightful, only approximate the underlying dynamics. In contrast, data-driven methods can extract more accurate low-dimensional representations, but it remains unclear when stability and safety properties observed in the latent space meaningfully transfer back to the full-order system. To bridge this gap, we introduce HALO (Hybrid Auto-encoded Locomotion), a framework for learning latent reduced-order models of periodic hybrid dynamics directly from trajectory data. HALO employs an autoencoder to identify a low-dimensional latent state together with a learned latent Poincaré map that captures step-to-step locomotion dynamics. This enables Lyapunov analysis and the construction of an associated region of attraction in the latent space, both of which can be lifted back to the full-order state space through the decoder. Experiments on a simulated hopping robot and full-body humanoid locomotion demonstrate that HALO yields low-dimensional models that retain meaningful stability structure and predict full-order region-of-attraction boundaries.

Safety Guardrails in the Sky: Realizing Control Barrier Functions on the VISTA F-16 Jet

The advancement of autonomous systems -- from legged robots to self-driving vehicles and aircraft -- necessitates executing increasingly high-performance and dynamic motions without ever putting the system or its environment in harm's way. In this paper, we introduce Guardrails -- a novel runtime assurance mechanism that guarantees dynamic safety for autonomous systems, allowing them to safely evolve on the edge of their operational domains. Rooted in the theory of control barrier functions, Guardrails offers a control strategy that carefully blends commands from a human or AI operator with safe control actions to guarantee safe behavior. To demonstrate its capabilities, we implemented Guardrails on an F-16 fighter jet and conducted flight tests where Guardrails supervised a human pilot to enforce g-limits, altitude bounds, geofence constraints, and combinations thereof. Throughout extensive flight testing, Guardrails successfully ensured safety, keeping the pilot in control when safe to do so and minimally modifying unsafe pilot inputs otherwise.

Input-to-State Safe Backstepping: Robust Safety-Critical Control with Unmatched Uncertainties

Guaranteeing safety in the presence of unmatched disturbances -- uncertainties that cannot be directly canceled by the control input -- remains a key challenge in nonlinear control. This paper presents a constructive approach to safety-critical control of nonlinear systems with unmatched disturbances. We first present a generalization of the input-to-state safety (ISSf) framework for systems with these uncertainties using the recently developed notion of an Optimal Decay CBF, which provides more flexibility for satisfying the associated Lyapunov-like conditions for safety. From there, we outline a procedure for constructing ISSf-CBFs for two relevant classes of systems with unmatched uncertainties: i) strict-feedback systems; ii) dual-relative-degree systems, which are similar to differentially flat systems. Our theoretical results are illustrated via numerical simulations of an inverted pendulum and planar quadrotor.

Compatibility of Multiple Control Barrier Functions for Constrained Nonlinear Systems

Control barrier functions (CBFs) are a powerful tool for the constrained control of nonlinear systems; however, the majority of results in the literature focus on systems subject to a single CBF constraint, making it challenging to synthesize provably safe controllers that handle multiple state constraints. This paper presents a framework for constrained control of nonlinear systems subject to box constraints on the systems' vector-valued outputs using multiple CBFs. Our results illustrate that when the output has a vector relative degree, the CBF constraints encoding these box constraints are compatible, and the resulting optimization-based controller is locally Lipschitz continuous and admits a closed-form expression. Additional results are presented to characterize the degradation of nominal tracking objectives in the presence of safety constraints. Simulations of a planar quadrotor are presented to demonstrate the efficacy of the proposed framework.

Learning for Layered Safety-Critical Control with Predictive Control Barrier Functions

Safety filters leveraging control barrier functions (CBFs) are highly effective for enforcing safe behavior on complex systems. It is often easier to synthesize CBFs for a Reduced order Model (RoM), and track the resulting safe behavior on the Full order Model (FoM) -- yet gaps between the RoM and FoM can result in safety violations. This paper introduces \emph{predictive CBFs} to address this gap by leveraging rollouts of the FoM to define a predictive robustness term added to the RoM CBF condition. Theoretically, we prove that this guarantees safety in a layered control implementation. Practically, we learn the predictive robustness term through massive parallel simulation with domain randomization. We demonstrate in simulation that this yields safe FoM behavior with minimal conservatism, and experimentally realize predictive CBFs on a 3D hopping robot.

Safety-Critical Controller Synthesis with Reduced-Order Models

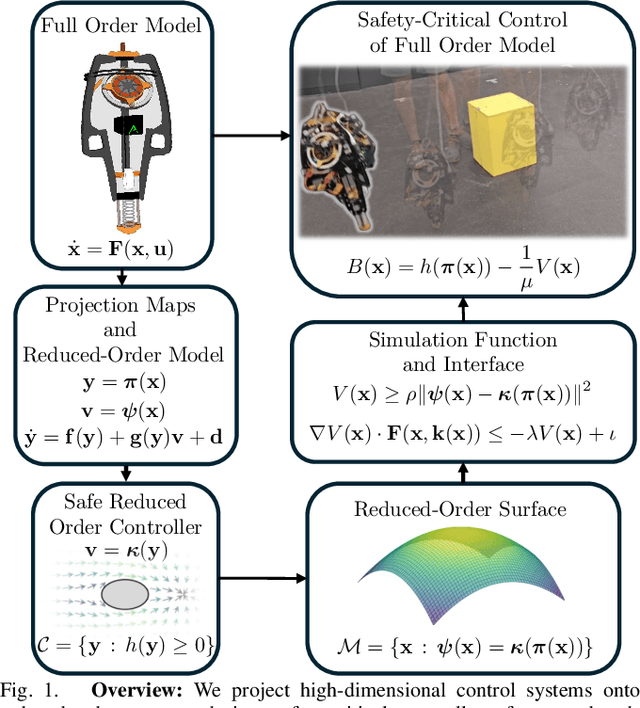
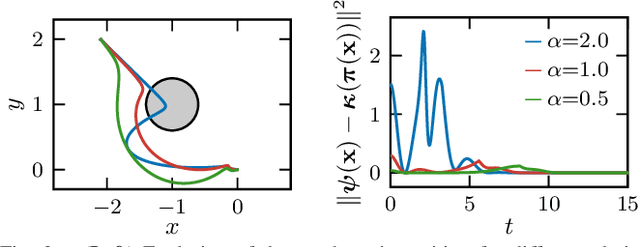
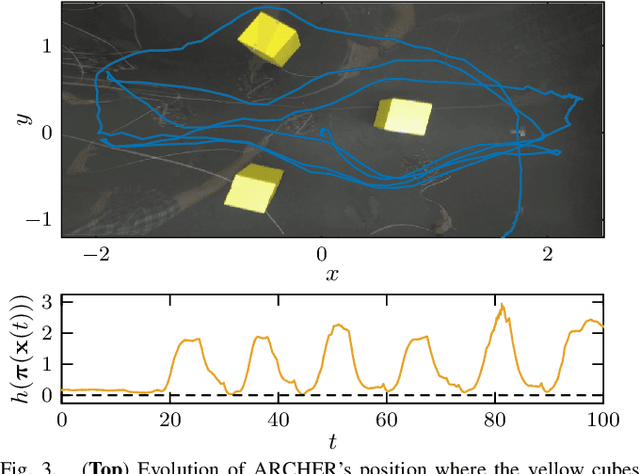
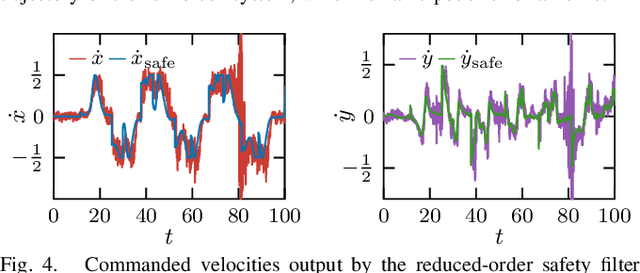
Reduced-order models (ROMs) provide lower dimensional representations of complex systems, capturing their salient features while simplifying control design. Building on previous work, this paper presents an overarching framework for the integration of ROMs and control barrier functions, enabling the use of simplified models to construct safety-critical controllers while providing safety guarantees for complex full-order models. To achieve this, we formalize the connection between full and ROMs by defining projection mappings that relate the states and inputs of these models and leverage simulation functions to establish conditions under which safety guarantees may be transferred from a ROM to its corresponding full-order model. The efficacy of our framework is illustrated through simulation results on a drone and hardware demonstrations on ARCHER, a 3D hopping robot.

Constructive Safety-Critical Control: Synthesizing Control Barrier Functions for Partially Feedback Linearizable Systems

Certifying the safety of nonlinear systems, through the lens of set invariance and control barrier functions (CBFs), offers a powerful method for controller synthesis, provided a CBF can be constructed. This paper draws connections between partial feedback linearization and CBF synthesis. We illustrate that when a control affine system is input-output linearizable with respect to a smooth output function, then, under mild regularity conditions, one may extend any safety constraint defined on the output to a CBF for the full-order dynamics. These more general results are specialized to robotic systems where the conditions required to synthesize CBFs simplify. The CBFs constructed from our approach are applied and verified in simulation and hardware experiments on a quadrotor.

Safety-Critical Control for Autonomous Systems: Control Barrier Functions via Reduced-Order Models

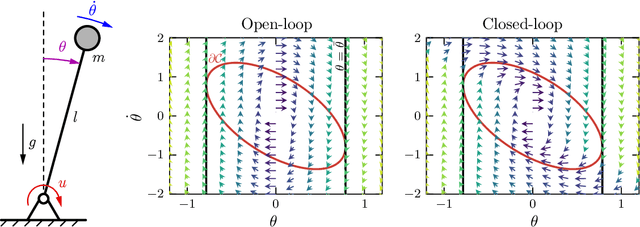
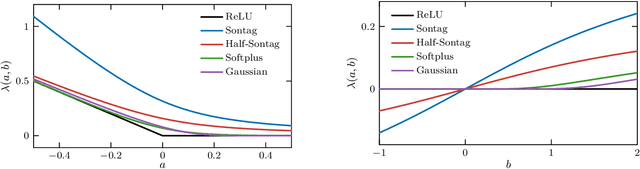
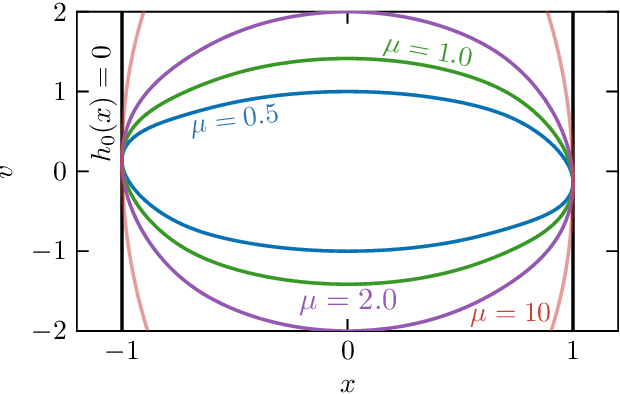
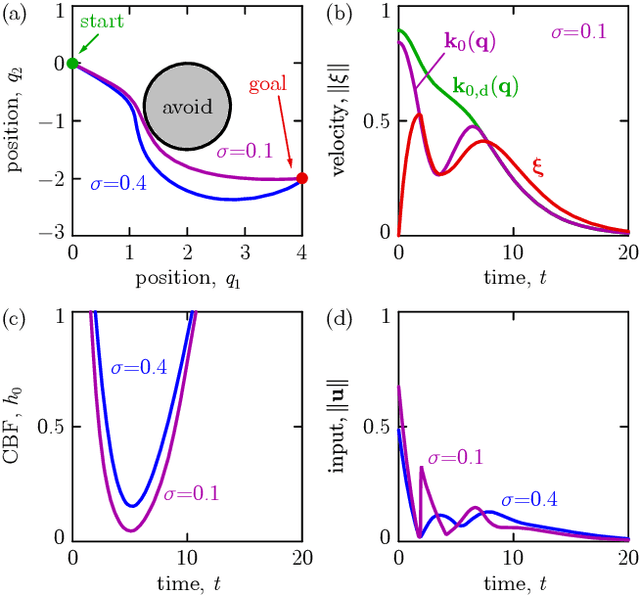
Modern autonomous systems, such as flying, legged, and wheeled robots, are generally characterized by high-dimensional nonlinear dynamics, which presents challenges for model-based safety-critical control design. Motivated by the success of reduced-order models in robotics, this paper presents a tutorial on constructive safety-critical control via reduced-order models and control barrier functions (CBFs). To this end, we provide a unified formulation of techniques in the literature that share a common foundation of constructing CBFs for complex systems from CBFs for much simpler systems. Such ideas are illustrated through formal results, simple numerical examples, and case studies of real-world systems to which these techniques have been experimentally applied.

Characterizing Smooth Safety Filters via the Implicit Function Theorem

Optimization-based safety filters, such as control barrier function (CBF) based quadratic programs (QPs), have demonstrated success in controlling autonomous systems to achieve complex goals. These CBF-QPs can be shown to be continuous, but are generally not smooth, let alone continuously differentiable. In this paper, we present a general characterization of smooth safety filters -- smooth controllers that guarantee safety in a minimally invasive fashion -- based on the Implicit Function Theorem. This characterization leads to families of smooth universal formulas for safety-critical controllers that quantify the conservatism of the resulting safety filter, the utility of which is demonstrated through illustrative examples.

High Order Robust Adaptive Control Barrier Functions and Exponentially Stabilizing Adaptive Control Lyapunov Functions

This paper studies the problem of utilizing data-driven adaptive control techniques to guarantee stability and safety of uncertain nonlinear systems with high relative degree. We first introduce the notion of a High Order Robust Adaptive Control Barrier Function (HO-RaCBF) as a means to compute control policies guaranteeing satisfaction of high relative degree safety constraints in the face of parametric model uncertainty. The developed approach guarantees safety by initially accounting for all possible parameter realizations but adaptively reduces uncertainty in the parameter estimates leveraging data recorded online. We then introduce the notion of an Exponentially Stabilizing Adaptive Control Lyapunov Function (ES-aCLF) that leverages the same data as the HO-RaCBF controller to guarantee exponential convergence of the system trajectory. The developed HO-RaCBF and ES-aCLF are unified in a quadratic programming framework, whose efficacy is showcased via two numerical examples that, to our knowledge, cannot be addressed by existing adaptive control barrier function techniques.