Enabling Safety for Aerial Robots: Planning and Control Architectures

Ensuring safe autonomy is crucial for deploying aerial robots in real-world applications. However, safety is a multifaceted challenge that must be addressed from multiple perspectives, including navigation in dynamic environments, operation under resource constraints, and robustness against adversarial attacks and uncertainties. In this paper, we present the authors' recent work that tackles some of these challenges and highlights key aspects that must be considered to enhance the safety and performance of autonomous aerial systems. All presented approaches are validated through hardware experiments.

Multi-Agent Clarity-Aware Dynamic Coverage with Gaussian Processes

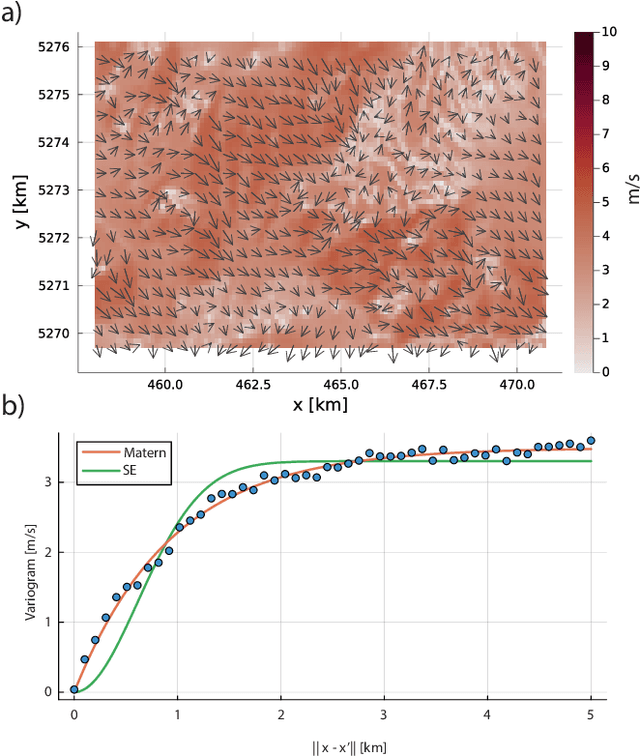
This paper presents two algorithms for multi-agent dynamic coverage in spatiotemporal environments, where the coverage algorithms are informed by the method of data assimilation. In particular, we show that by considering the information assimilation algorithm, here a Numerical Gaussian Process Kalman Filter, the influence of measurements taken at one position on the uncertainty of the estimate at another location can be computed. We use this relationship to propose new coverage algorithms. Furthermore, we show that the controllers naturally extend to the multi-agent context, allowing for a distributed-control central-information paradigm for multi-agent coverage. Finally, we demonstrate the algorithms through a realistic simulation of a team of UAVs collecting wind data over a region in Austria.

A Constructive Method for Designing Safe Multirate Controllers for Differentially-Flat Systems

We present a multi-rate control architecture that leverages fundamental properties of differential flatness to synthesize controllers for safety-critical nonlinear dynamical systems. We propose a two-layer architecture, where the high-level generates reference trajectories using a linear Model Predictive Controller, and the low-level tracks this reference using a feedback controller. The novelty lies in how we couple these layers, to achieve formal guarantees on recursive feasibility of the MPC problem, and safety of the nonlinear system. Furthermore, using differential flatness, we provide a constructive means to synthesize the multi-rate controller, thereby removing the need to search for suitable Lyapunov or barrier functions, or to approximately linearize/discretize nonlinear dynamics. We show the synthesized controller is a convex optimization problem, making it amenable to real-time implementations. The method is demonstrated experimentally on a ground rover and a quadruped robotic system.

Safe and Robust Observer-Controller Synthesis using Control Barrier Functions

This paper addresses the synthesis of safety-critical controllers using estimate feedback. We propose an observer-controller interconnection to ensure that the nonlinear system remains safe despite bounded disturbances on the system dynamics and measurements that correspond to partial state information. The co-design of observers and controllers is critical, since even in undisturbed cases, observers and controllers designed independently may not render the system safe. We propose two approaches to synthesize observer-controller interconnections. The first approach utilizes Input-to-State Stable observers, and the second uses Bounded Error observers. Using these stability and boundedness properties of the observation error, we construct novel Control Barrier Functions that impose inequality constraints on the control inputs which, when satisfied, certifies safety. We propose quadratic program-based controllers to satisfy these constraints, and prove Lipschitz continuity of the derived controllers. Simulations and experiments on a quadrotor demonstrate the efficacy of the proposed methods.