Robust Markov Decision Processes: A Place Where AI and Formal Methods Meet

Markov decision processes (MDPs) are a standard model for sequential decision-making problems and are widely used across many scientific areas, including formal methods and artificial intelligence (AI). MDPs do, however, come with the restrictive assumption that the transition probabilities need to be precisely known. Robust MDPs (RMDPs) overcome this assumption by instead defining the transition probabilities to belong to some uncertainty set. We present a gentle survey on RMDPs, providing a tutorial covering their fundamentals. In particular, we discuss RMDP semantics and how to solve them by extending standard MDP methods such as value iteration and policy iteration. We also discuss how RMDPs relate to other models and how they are used in several contexts, including reinforcement learning and abstraction techniques. We conclude with some challenges for future work on RMDPs.

Pessimistic Iterative Planning for Robust POMDPs

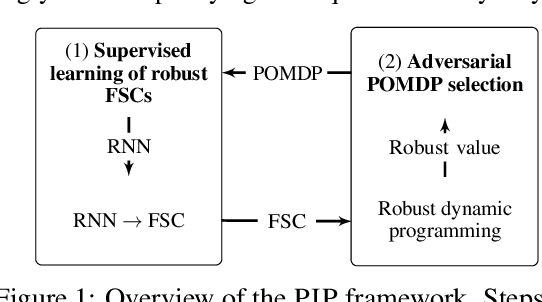
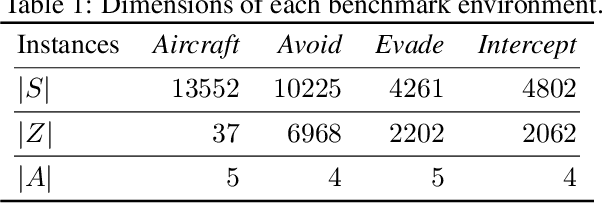
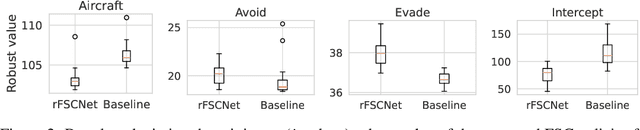
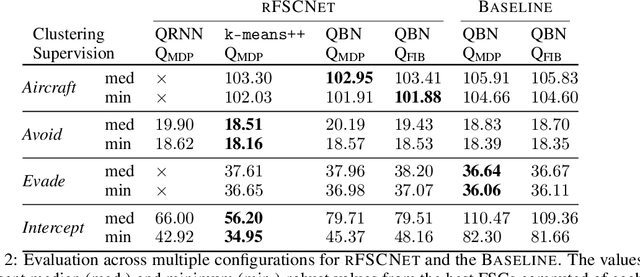
Robust partially observable Markov decision processes (robust POMDPs) extend classical POMDPs to handle additional uncertainty on the transition and observation probabilities via so-called uncertainty sets. Policies for robust POMDPs must not only be memory-based to account for partial observability but also robust against model uncertainty to account for the worst-case instances from the uncertainty sets. We propose the pessimistic iterative planning (PIP) framework, which finds robust memory-based policies for robust POMDPs. PIP alternates between two main steps: (1) selecting an adversarial (non-robust) POMDP via worst-case probability instances from the uncertainty sets; and (2) computing a finite-state controller (FSC) for this adversarial POMDP. We evaluate the performance of this FSC on the original robust POMDP and use this evaluation in step (1) to select the next adversarial POMDP. Within PIP, we propose the rFSCNet algorithm. In each iteration, rFSCNet finds an FSC through a recurrent neural network trained using supervision policies optimized for the adversarial POMDP. The empirical evaluation in four benchmark environments showcases improved robustness against a baseline method in an ablation study and competitive performance compared to a state-of-the-art robust POMDP solver.

Imprecise Probabilities Meet Partial Observability: Game Semantics for Robust POMDPs

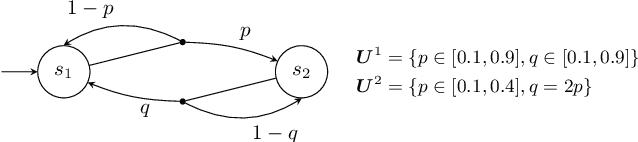
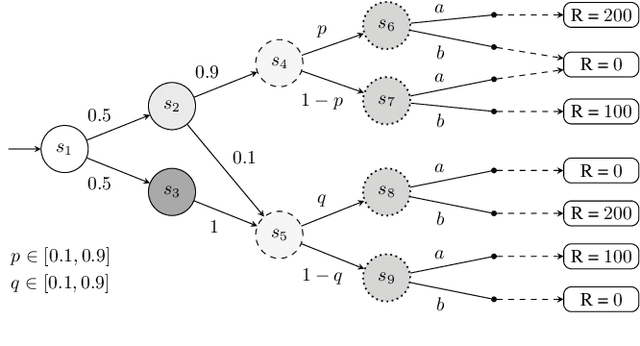
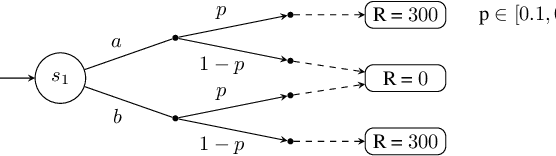
Partially observable Markov decision processes (POMDPs) rely on the key assumption that probability distributions are precisely known. Robust POMDPs (RPOMDPs) alleviate this concern by defining imprecise probabilities, referred to as uncertainty sets. While robust MDPs have been studied extensively, work on RPOMDPs is limited and primarily focuses on algorithmic solution methods. We expand the theoretical understanding of RPOMDPs by showing that 1) different assumptions on the uncertainty sets affect optimal policies and values; 2) RPOMDPs have a partially observable stochastic game (POSG) semantic; and 3) the same RPOMDP with different assumptions leads to semantically different POSGs and, thus, different policies and values. These novel semantics for RPOMDPS give access to results for the widely studied POSG model; concretely, we show the existence of a Nash equilibrium. Finally, we classify the existing RPOMDP literature using our semantics, clarifying under which uncertainty assumptions these existing works operate.

More for Less: Safe Policy Improvement With Stronger Performance Guarantees

In an offline reinforcement learning setting, the safe policy improvement (SPI) problem aims to improve the performance of a behavior policy according to which sample data has been generated. State-of-the-art approaches to SPI require a high number of samples to provide practical probabilistic guarantees on the improved policy's performance. We present a novel approach to the SPI problem that provides the means to require less data for such guarantees. Specifically, to prove the correctness of these guarantees, we devise implicit transformations on the data set and the underlying environment model that serve as theoretical foundations to derive tighter improvement bounds for SPI. Our empirical evaluation, using the well-established SPI with baseline bootstrapping (SPIBB) algorithm, on standard benchmarks shows that our method indeed significantly reduces the sample complexity of the SPIBB algorithm.

Decision-Making Under Uncertainty: Beyond Probabilities

This position paper reflects on the state-of-the-art in decision-making under uncertainty. A classical assumption is that probabilities can sufficiently capture all uncertainty in a system. In this paper, the focus is on the uncertainty that goes beyond this classical interpretation, particularly by employing a clear distinction between aleatoric and epistemic uncertainty. The paper features an overview of Markov decision processes (MDPs) and extensions to account for partial observability and adversarial behavior. These models sufficiently capture aleatoric uncertainty but fail to account for epistemic uncertainty robustly. Consequently, we present a thorough overview of so-called uncertainty models that exhibit uncertainty in a more robust interpretation. We show several solution techniques for both discrete and continuous models, ranging from formal verification, over control-based abstractions, to reinforcement learning. As an integral part of this paper, we list and discuss several key challenges that arise when dealing with rich types of uncertainty in a model-based fashion.

Safe Policy Improvement for POMDPs via Finite-State Controllers

We study safe policy improvement (SPI) for partially observable Markov decision processes (POMDPs). SPI is an offline reinforcement learning (RL) problem that assumes access to (1) historical data about an environment, and (2) the so-called behavior policy that previously generated this data by interacting with the environment. SPI methods neither require access to a model nor the environment itself, and aim to reliably improve the behavior policy in an offline manner. Existing methods make the strong assumption that the environment is fully observable. In our novel approach to the SPI problem for POMDPs, we assume that a finite-state controller (FSC) represents the behavior policy and that finite memory is sufficient to derive optimal policies. This assumption allows us to map the POMDP to a finite-state fully observable MDP, the history MDP. We estimate this MDP by combining the historical data and the memory of the FSC, and compute an improved policy using an off-the-shelf SPI algorithm. The underlying SPI method constrains the policy-space according to the available data, such that the newly computed policy only differs from the behavior policy when sufficient data was available. We show that this new policy, converted into a new FSC for the (unknown) POMDP, outperforms the behavior policy with high probability. Experimental results on several well-established benchmarks show the applicability of the approach, even in cases where finite memory is not sufficient.

Robust Anytime Learning of Markov Decision Processes

Markov decision processes (MDPs) are formal models commonly used in sequential decision-making. MDPs capture the stochasticity that may arise, for instance, from imprecise actuators via probabilities in the transition function. However, in data-driven applications, deriving precise probabilities from (limited) data introduces statistical errors that may lead to unexpected or undesirable outcomes. Uncertain MDPs (uMDPs) do not require precise probabilities but instead use so-called uncertainty sets in the transitions, accounting for such limited data. Tools from the formal verification community efficiently compute robust policies that provably adhere to formal specifications, like safety constraints, under the worst-case instance in the uncertainty set. We continuously learn the transition probabilities of an MDP in a robust anytime-learning approach that combines a dedicated Bayesian inference scheme with the computation of robust policies. In particular, our method (1) approximates probabilities as intervals, (2) adapts to new data that may be inconsistent with an intermediate model, and (3) may be stopped at any time to compute a robust policy on the uMDP that faithfully captures the data so far. We show the effectiveness of our approach and compare it to robust policies computed on uMDPs learned by the UCRL2 reinforcement learning algorithm in an experimental evaluation on several benchmarks.

Robust Finite-State Controllers for Uncertain POMDPs

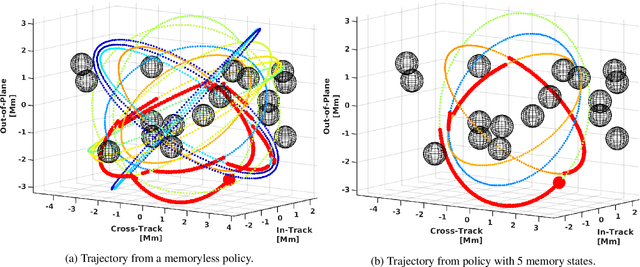
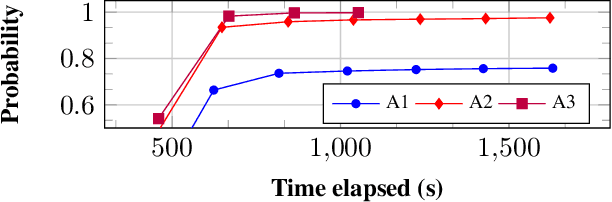
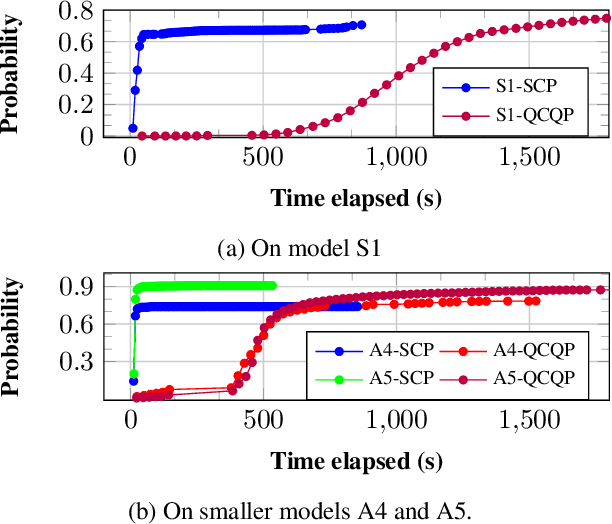
Uncertain partially observable Markov decision processes (uPOMDPs) allow the probabilistic transition and observation functions of standard POMDPs to belong to a so-called uncertainty set. Such uncertainty sets capture uncountable sets of probability distributions. We develop an algorithm to compute finite-memory policies for uPOMDPs that robustly satisfy given specifications against any admissible distribution. In general, computing such policies is both theoretically and practically intractable. We provide an efficient solution to this problem in four steps. (1) We state the underlying problem as a nonconvex optimization problem with infinitely many constraints. (2) A dedicated dualization scheme yields a dual problem that is still nonconvex but has finitely many constraints. (3) We linearize this dual problem and (4) solve the resulting finite linear program to obtain locally optimal solutions to the original problem. The resulting problem formulation is exponentially smaller than those resulting from existing methods. We demonstrate the applicability of our algorithm using large instances of an aircraft collision-avoidance scenario and a novel spacecraft motion planning case study.