Robust Markov Decision Processes: A Place Where AI and Formal Methods Meet

Markov decision processes (MDPs) are a standard model for sequential decision-making problems and are widely used across many scientific areas, including formal methods and artificial intelligence (AI). MDPs do, however, come with the restrictive assumption that the transition probabilities need to be precisely known. Robust MDPs (RMDPs) overcome this assumption by instead defining the transition probabilities to belong to some uncertainty set. We present a gentle survey on RMDPs, providing a tutorial covering their fundamentals. In particular, we discuss RMDP semantics and how to solve them by extending standard MDP methods such as value iteration and policy iteration. We also discuss how RMDPs relate to other models and how they are used in several contexts, including reinforcement learning and abstraction techniques. We conclude with some challenges for future work on RMDPs.

Imprecise Probabilities Meet Partial Observability: Game Semantics for Robust POMDPs

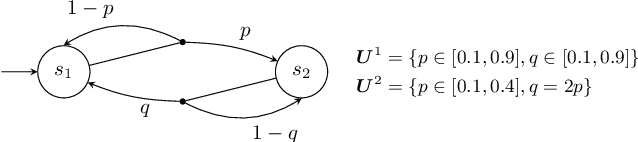
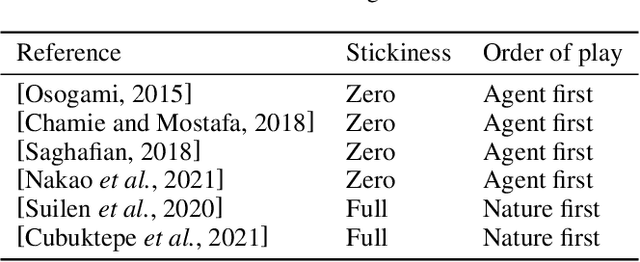
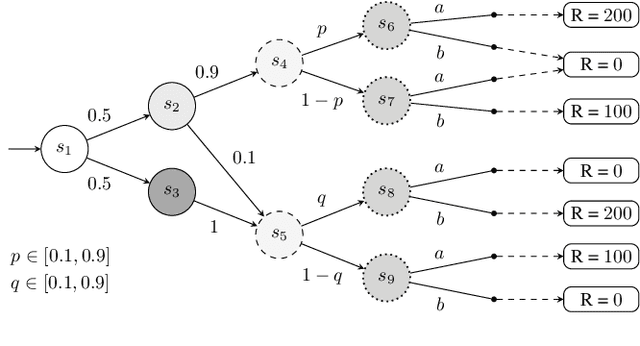
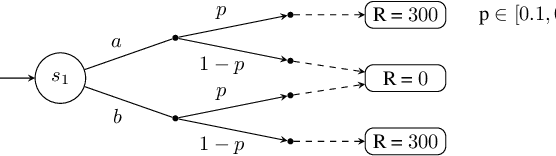
Partially observable Markov decision processes (POMDPs) rely on the key assumption that probability distributions are precisely known. Robust POMDPs (RPOMDPs) alleviate this concern by defining imprecise probabilities, referred to as uncertainty sets. While robust MDPs have been studied extensively, work on RPOMDPs is limited and primarily focuses on algorithmic solution methods. We expand the theoretical understanding of RPOMDPs by showing that 1) different assumptions on the uncertainty sets affect optimal policies and values; 2) RPOMDPs have a partially observable stochastic game (POSG) semantic; and 3) the same RPOMDP with different assumptions leads to semantically different POSGs and, thus, different policies and values. These novel semantics for RPOMDPS give access to results for the widely studied POSG model; concretely, we show the existence of a Nash equilibrium. Finally, we classify the existing RPOMDP literature using our semantics, clarifying under which uncertainty assumptions these existing works operate.