Robust Markov Decision Processes: A Place Where AI and Formal Methods Meet

Markov decision processes (MDPs) are a standard model for sequential decision-making problems and are widely used across many scientific areas, including formal methods and artificial intelligence (AI). MDPs do, however, come with the restrictive assumption that the transition probabilities need to be precisely known. Robust MDPs (RMDPs) overcome this assumption by instead defining the transition probabilities to belong to some uncertainty set. We present a gentle survey on RMDPs, providing a tutorial covering their fundamentals. In particular, we discuss RMDP semantics and how to solve them by extending standard MDP methods such as value iteration and policy iteration. We also discuss how RMDPs relate to other models and how they are used in several contexts, including reinforcement learning and abstraction techniques. We conclude with some challenges for future work on RMDPs.

Learning-Based Verification of Stochastic Dynamical Systems with Neural Network Policies

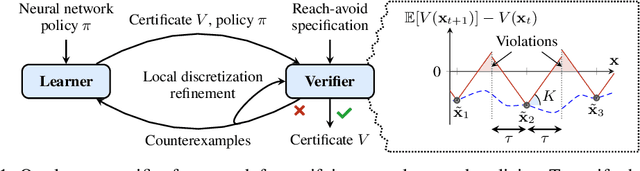
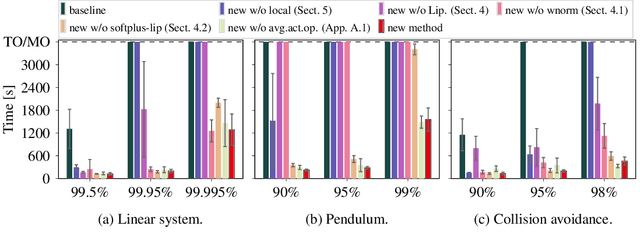
We consider the verification of neural network policies for reach-avoid control tasks in stochastic dynamical systems. We use a verification procedure that trains another neural network, which acts as a certificate proving that the policy satisfies the task. For reach-avoid tasks, it suffices to show that this certificate network is a reach-avoid supermartingale (RASM). As our main contribution, we significantly accelerate algorithmic approaches for verifying that a neural network is indeed a RASM. The main bottleneck of these approaches is the discretization of the state space of the dynamical system. The following two key contributions allow us to use a coarser discretization than existing approaches. First, we present a novel and fast method to compute tight upper bounds on Lipschitz constants of neural networks based on weighted norms. We further improve these bounds on Lipschitz constants based on the characteristics of the certificate network. Second, we integrate an efficient local refinement scheme that dynamically refines the state space discretization where necessary. Our empirical evaluation shows the effectiveness of our approach for verifying neural network policies in several benchmarks and trained with different reinforcement learning algorithms.

Correct-by-Construction Control for Stochastic and Uncertain Dynamical Models via Formal Abstractions

Automated synthesis of correct-by-construction controllers for autonomous systems is crucial for their deployment in safety-critical scenarios. Such autonomous systems are naturally modeled as stochastic dynamical models. The general problem is to compute a controller that provably satisfies a given task, represented as a probabilistic temporal logic specification. However, factors such as stochastic uncertainty, imprecisely known parameters, and hybrid features make this problem challenging. We have developed an abstraction framework that can be used to solve this problem under various modeling assumptions. Our approach is based on a robust finite-state abstraction of the stochastic dynamical model in the form of a Markov decision process with intervals of probabilities (iMDP). We use state-of-the-art verification techniques to compute an optimal policy on the iMDP with guarantees for satisfying the given specification. We then show that, by construction, we can refine this policy into a feedback controller for which these guarantees carry over to the dynamical model. In this short paper, we survey our recent research in this area and highlight two challenges (related to scalability and dealing with nonlinear dynamics) that we aim to address with our ongoing research.

Efficient Sensitivity Analysis for Parametric Robust Markov Chains

We provide a novel method for sensitivity analysis of parametric robust Markov chains. These models incorporate parameters and sets of probability distributions to alleviate the often unrealistic assumption that precise probabilities are available. We measure sensitivity in terms of partial derivatives with respect to the uncertain transition probabilities regarding measures such as the expected reward. As our main contribution, we present an efficient method to compute these partial derivatives. To scale our approach to models with thousands of parameters, we present an extension of this method that selects the subset of $k$ parameters with the highest partial derivative. Our methods are based on linear programming and differentiating these programs around a given value for the parameters. The experiments show the applicability of our approach on models with over a million states and thousands of parameters. Moreover, we embed the results within an iterative learning scheme that profits from having access to a dedicated sensitivity analysis.

Decision-Making Under Uncertainty: Beyond Probabilities

This position paper reflects on the state-of-the-art in decision-making under uncertainty. A classical assumption is that probabilities can sufficiently capture all uncertainty in a system. In this paper, the focus is on the uncertainty that goes beyond this classical interpretation, particularly by employing a clear distinction between aleatoric and epistemic uncertainty. The paper features an overview of Markov decision processes (MDPs) and extensions to account for partial observability and adversarial behavior. These models sufficiently capture aleatoric uncertainty but fail to account for epistemic uncertainty robustly. Consequently, we present a thorough overview of so-called uncertainty models that exhibit uncertainty in a more robust interpretation. We show several solution techniques for both discrete and continuous models, ranging from formal verification, over control-based abstractions, to reinforcement learning. As an integral part of this paper, we list and discuss several key challenges that arise when dealing with rich types of uncertainty in a model-based fashion.

Robust Control for Dynamical Systems With Non-Gaussian Noise via Formal Abstractions

Controllers for dynamical systems that operate in safety-critical settings must account for stochastic disturbances. Such disturbances are often modeled as process noise in a dynamical system, and common assumptions are that the underlying distributions are known and/or Gaussian. In practice, however, these assumptions may be unrealistic and can lead to poor approximations of the true noise distribution. We present a novel controller synthesis method that does not rely on any explicit representation of the noise distributions. In particular, we address the problem of computing a controller that provides probabilistic guarantees on safely reaching a target, while also avoiding unsafe regions of the state space. First, we abstract the continuous control system into a finite-state model that captures noise by probabilistic transitions between discrete states. As a key contribution, we adapt tools from the scenario approach to compute probably approximately correct (PAC) bounds on these transition probabilities, based on a finite number of samples of the noise. We capture these bounds in the transition probability intervals of a so-called interval Markov decision process (iMDP). This iMDP is, with a user-specified confidence probability, robust against uncertainty in the transition probabilities, and the tightness of the probability intervals can be controlled through the number of samples. We use state-of-the-art verification techniques to provide guarantees on the iMDP and compute a controller for which these guarantees carry over to the original control system. In addition, we develop a tailored computational scheme that reduces the complexity of the synthesis of these guarantees on the iMDP. Benchmarks on realistic control systems show the practical applicability of our method, even when the iMDP has hundreds of millions of transitions.

Formal Controller Synthesis for Markov Jump Linear Systems with Uncertain Dynamics

Automated synthesis of provably correct controllers for cyber-physical systems is crucial for deploying these systems in safety-critical scenarios. However, their hybrid features and stochastic or unknown behaviours make this synthesis problem challenging. In this paper, we propose a method for synthesizing controllers for Markov jump linear systems (MJLSs), a particular class of cyber-physical systems, that certifiably satisfy a requirement expressed as a specification in probabilistic computation tree logic (PCTL). An MJLS consists of a finite set of linear dynamics with unknown additive disturbances, where jumps between these modes are governed by a Markov decision process (MDP). We consider both the case where the transition function of this MDP is given by probability intervals or where it is completely unknown. Our approach is based on generating a finite-state abstraction which captures both the discrete and the continuous behaviour of the original system. We formalise such abstraction as an interval Markov decision process (iMDP): intervals of transition probabilities are computed using sampling techniques from the so-called "scenario approach", resulting in a probabilistically sound approximation of the MJLS. This iMDP abstracts both the jump dynamics between modes, as well as the continuous dynamics within the modes. To demonstrate the efficacy of our technique, we apply our method to multiple realistic benchmark problems, in particular, temperature control, and aerial vehicle delivery problems.

Probabilities Are Not Enough: Formal Controller Synthesis for Stochastic Dynamical Models with Epistemic Uncertainty

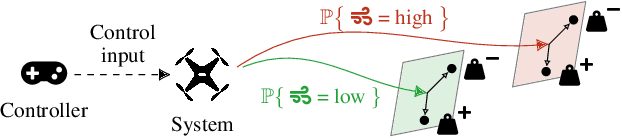
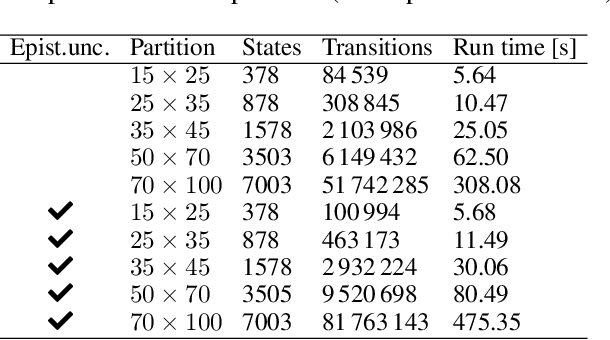
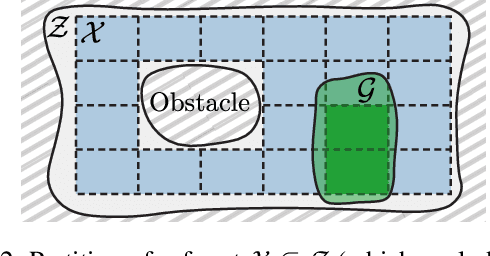
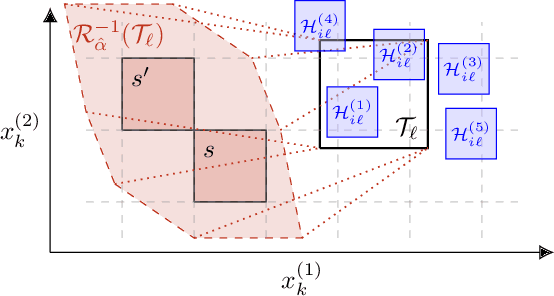
Capturing uncertainty in models of complex dynamical systems is crucial to designing safe controllers. Stochastic noise causes aleatoric uncertainty, whereas imprecise knowledge of model parameters and the presence of external disturbances lead to epistemic uncertainty. Several approaches use formal abstractions to synthesize policies that satisfy temporal specifications related to safety and reachability. However, the underlying models exclusively capture aleatoric but not epistemic uncertainty, and thus require that model parameters and disturbances are known precisely. Our contribution to overcoming this restriction is a novel abstraction-based controller synthesis method for continuous-state models with stochastic noise, uncertain parameters, and external disturbances. By sampling techniques and robust analysis, we capture both aleatoric and epistemic uncertainty, with a user-specified confidence level, in the transition probability intervals of a so-called interval Markov decision process (iMDP). We then synthesize an optimal policy on this abstract iMDP, which translates (with the specified confidence level) to a feedback controller for the continuous model, with the same performance guarantees. Our experimental benchmarks confirm that accounting for epistemic uncertainty leads to controllers that are more robust against variations in parameter values.