Provably Correct Sensor-driven Path-following for Unicycles using Monotonic Score Functions

This paper develops a provably stable sensor-driven controller for path-following applications of robots with unicycle kinematics, one specific class of which is the wheeled mobile robot (WMR). The sensor measurement is converted to a scalar value (the score) through some mapping (the score function); the latter may be designed or learned. The score is then mapped to forward and angular velocities using a simple rule with three parameters. The key contribution is that the correctness of this controller only relies on the score function satisfying monotonicity conditions with respect to the underlying state -- local path coordinates -- instead of achieving specific values at all states. The monotonicity conditions may be checked online by moving the WMR, without state estimation, or offline using a generative model of measurements such as in a simulator. Our approach provides both the practicality of a purely measurement-based control and the correctness of state-based guarantees. We demonstrate the effectiveness of this path-following approach on both a simulated and a physical WMR that use a learned score function derived from a binary classifier trained on real depth images.

Robust Control for Dynamical Systems With Non-Gaussian Noise via Formal Abstractions

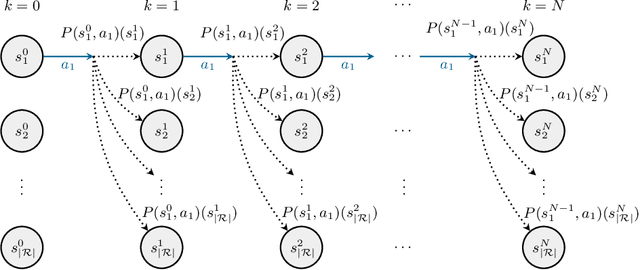
Controllers for dynamical systems that operate in safety-critical settings must account for stochastic disturbances. Such disturbances are often modeled as process noise in a dynamical system, and common assumptions are that the underlying distributions are known and/or Gaussian. In practice, however, these assumptions may be unrealistic and can lead to poor approximations of the true noise distribution. We present a novel controller synthesis method that does not rely on any explicit representation of the noise distributions. In particular, we address the problem of computing a controller that provides probabilistic guarantees on safely reaching a target, while also avoiding unsafe regions of the state space. First, we abstract the continuous control system into a finite-state model that captures noise by probabilistic transitions between discrete states. As a key contribution, we adapt tools from the scenario approach to compute probably approximately correct (PAC) bounds on these transition probabilities, based on a finite number of samples of the noise. We capture these bounds in the transition probability intervals of a so-called interval Markov decision process (iMDP). This iMDP is, with a user-specified confidence probability, robust against uncertainty in the transition probabilities, and the tightness of the probability intervals can be controlled through the number of samples. We use state-of-the-art verification techniques to provide guarantees on the iMDP and compute a controller for which these guarantees carry over to the original control system. In addition, we develop a tailored computational scheme that reduces the complexity of the synthesis of these guarantees on the iMDP. Benchmarks on realistic control systems show the practical applicability of our method, even when the iMDP has hundreds of millions of transitions.

Sampling-Based Robust Control of Autonomous Systems with Non-Gaussian Noise

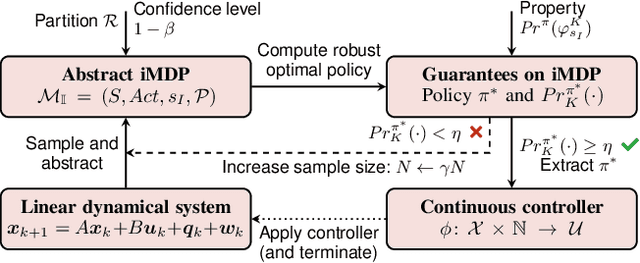
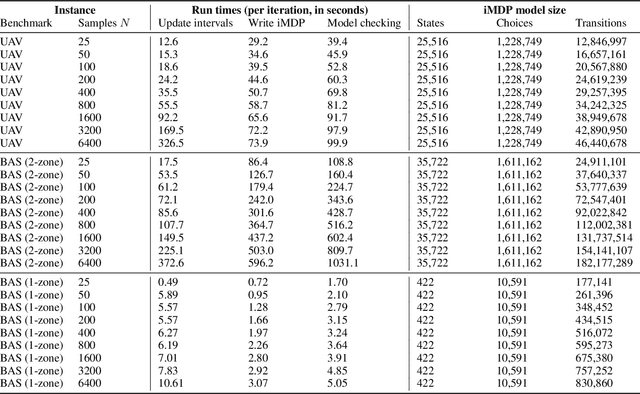
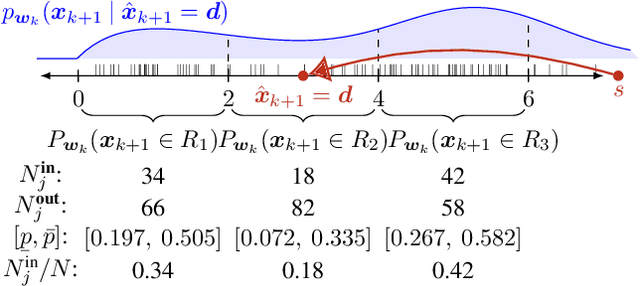
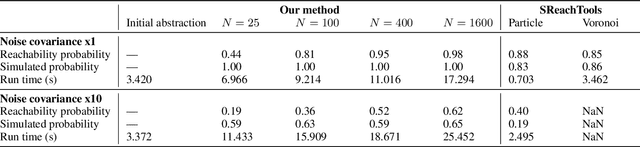
Controllers for autonomous systems that operate in safety-critical settings must account for stochastic disturbances. Such disturbances are often modelled as process noise, and common assumptions are that the underlying distributions are known and/or Gaussian. In practice, however, these assumptions may be unrealistic and can lead to poor approximations of the true noise distribution. We present a novel planning method that does not rely on any explicit representation of the noise distributions. In particular, we address the problem of computing a controller that provides probabilistic guarantees on safely reaching a target. First, we abstract the continuous system into a discrete-state model that captures noise by probabilistic transitions between states. As a key contribution, we adapt tools from the scenario approach to compute probably approximately correct (PAC) bounds on these transition probabilities, based on a finite number of samples of the noise. We capture these bounds in the transition probability intervals of a so-called interval Markov decision process (iMDP). This iMDP is robust against uncertainty in the transition probabilities, and the tightness of the probability intervals can be controlled through the number of samples. We use state-of-the-art verification techniques to provide guarantees on the iMDP, and compute a controller for which these guarantees carry over to the autonomous system. Realistic benchmarks show the practical applicability of our method, even when the iMDP has millions of states or transitions.

Filter-Based Abstractions with Correctness Guarantees for Planning under Uncertainty

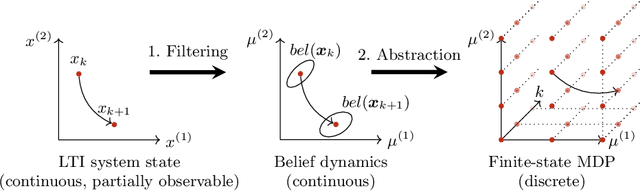
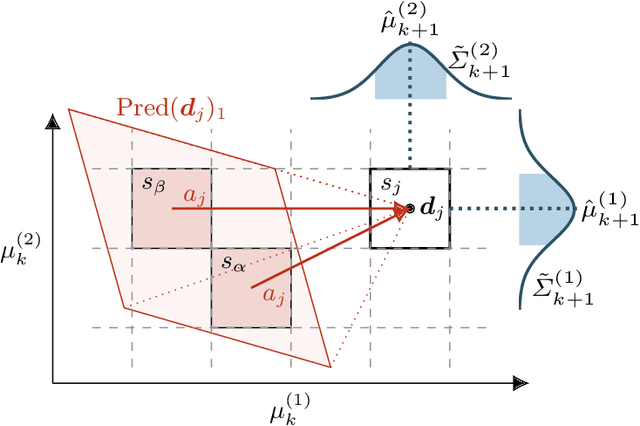
We study planning problems for continuous control systems with uncertainty caused by measurement and process noise. The goal is to find an optimal plan that guarantees that the system reaches a desired goal state within finite time. Measurement noise causes limited observability of system states, and process noise causes uncertainty in the outcome of a given plan. These factors render the problem undecidable in general. Our key contribution is a novel abstraction scheme that employs Kalman filtering as a state estimator to obtain a finite-state model, which we formalize as a Markov decision process (MDP). For this MDP, we employ state-of-the-art model checking techniques to efficiently compute plans that maximize the probability of reaching goal states. Moreover, we account for numerical imprecision in computing the abstraction by extending the MDP with intervals of probabilities as a more robust model. We show the correctness of the abstraction and provide several optimizations that aim to balance the quality of the plan and the scalability of the approach. We demonstrate that our method can handle systems that result in MDPs with thousands of states and millions of transitions.