Maintenance Strategies for Sewer Pipes with Multi-State Degradation and Deep Reinforcement Learning

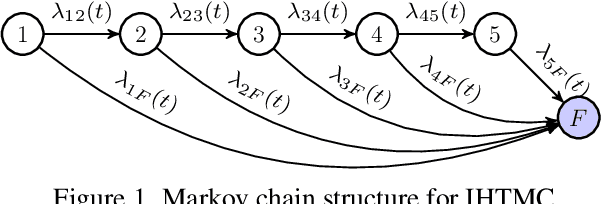
Large-scale infrastructure systems are crucial for societal welfare, and their effective management requires strategic forecasting and intervention methods that account for various complexities. Our study addresses two challenges within the Prognostics and Health Management (PHM) framework applied to sewer assets: modeling pipe degradation across severity levels and developing effective maintenance policies. We employ Multi-State Degradation Models (MSDM) to represent the stochastic degradation process in sewer pipes and use Deep Reinforcement Learning (DRL) to devise maintenance strategies. A case study of a Dutch sewer network exemplifies our methodology. Our findings demonstrate the model's effectiveness in generating intelligent, cost-saving maintenance strategies that surpass heuristics. It adapts its management strategy based on the pipe's age, opting for a passive approach for newer pipes and transitioning to active strategies for older ones to prevent failures and reduce costs. This research highlights DRL's potential in optimizing maintenance policies. Future research will aim improve the model by incorporating partial observability, exploring various reinforcement learning algorithms, and extending this methodology to comprehensive infrastructure management.

Robust Control for Dynamical Systems With Non-Gaussian Noise via Formal Abstractions

Controllers for dynamical systems that operate in safety-critical settings must account for stochastic disturbances. Such disturbances are often modeled as process noise in a dynamical system, and common assumptions are that the underlying distributions are known and/or Gaussian. In practice, however, these assumptions may be unrealistic and can lead to poor approximations of the true noise distribution. We present a novel controller synthesis method that does not rely on any explicit representation of the noise distributions. In particular, we address the problem of computing a controller that provides probabilistic guarantees on safely reaching a target, while also avoiding unsafe regions of the state space. First, we abstract the continuous control system into a finite-state model that captures noise by probabilistic transitions between discrete states. As a key contribution, we adapt tools from the scenario approach to compute probably approximately correct (PAC) bounds on these transition probabilities, based on a finite number of samples of the noise. We capture these bounds in the transition probability intervals of a so-called interval Markov decision process (iMDP). This iMDP is, with a user-specified confidence probability, robust against uncertainty in the transition probabilities, and the tightness of the probability intervals can be controlled through the number of samples. We use state-of-the-art verification techniques to provide guarantees on the iMDP and compute a controller for which these guarantees carry over to the original control system. In addition, we develop a tailored computational scheme that reduces the complexity of the synthesis of these guarantees on the iMDP. Benchmarks on realistic control systems show the practical applicability of our method, even when the iMDP has hundreds of millions of transitions.

Automatic inference of fault tree models via multi-objective evolutionary algorithms

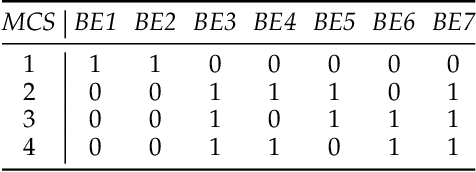
Fault tree analysis is a well-known technique in reliability engineering and risk assessment, which supports decision-making processes and the management of complex systems. Traditionally, fault tree (FT) models are built manually together with domain experts, considered a time-consuming process prone to human errors. With Industry 4.0, there is an increasing availability of inspection and monitoring data, making techniques that enable knowledge extraction from large data sets relevant. Thus, our goal with this work is to propose a data-driven approach to infer efficient FT structures that achieve a complete representation of the failure mechanisms contained in the failure data set without human intervention. Our algorithm, the FT-MOEA, based on multi-objective evolutionary algorithms, enables the simultaneous optimization of different relevant metrics such as the FT size, the error computed based on the failure data set and the Minimal Cut Sets. Our results show that, for six case studies from the literature, our approach successfully achieved automatic, efficient, and consistent inference of the associated FT models. We also present the results of a parametric analysis that tests our algorithm for different relevant conditions that influence its performance, as well as an overview of the data-driven methods used to automatically infer FT models.

Sampling-Based Robust Control of Autonomous Systems with Non-Gaussian Noise

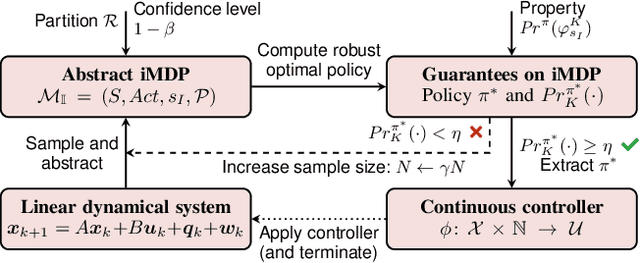
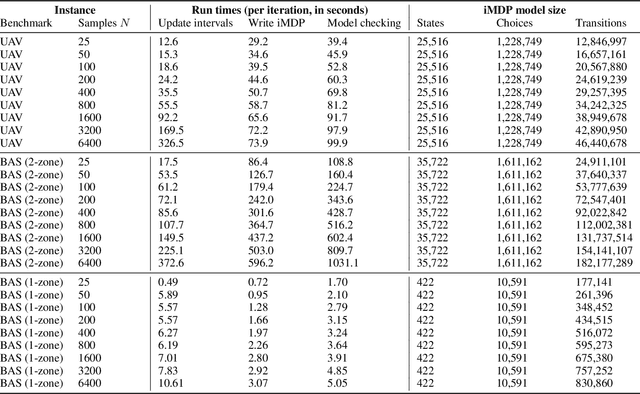
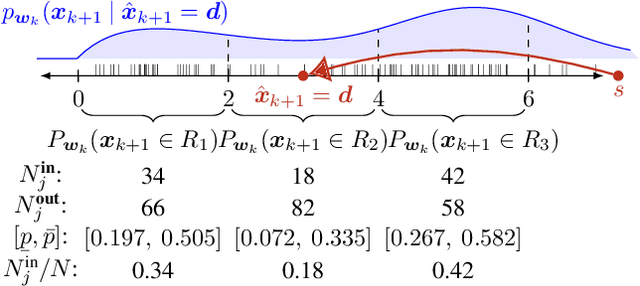
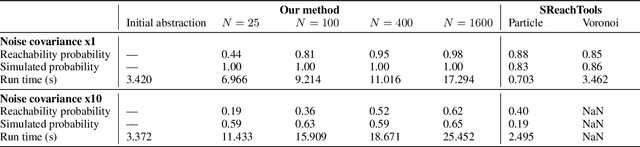
Controllers for autonomous systems that operate in safety-critical settings must account for stochastic disturbances. Such disturbances are often modelled as process noise, and common assumptions are that the underlying distributions are known and/or Gaussian. In practice, however, these assumptions may be unrealistic and can lead to poor approximations of the true noise distribution. We present a novel planning method that does not rely on any explicit representation of the noise distributions. In particular, we address the problem of computing a controller that provides probabilistic guarantees on safely reaching a target. First, we abstract the continuous system into a discrete-state model that captures noise by probabilistic transitions between states. As a key contribution, we adapt tools from the scenario approach to compute probably approximately correct (PAC) bounds on these transition probabilities, based on a finite number of samples of the noise. We capture these bounds in the transition probability intervals of a so-called interval Markov decision process (iMDP). This iMDP is robust against uncertainty in the transition probabilities, and the tightness of the probability intervals can be controlled through the number of samples. We use state-of-the-art verification techniques to provide guarantees on the iMDP, and compute a controller for which these guarantees carry over to the autonomous system. Realistic benchmarks show the practical applicability of our method, even when the iMDP has millions of states or transitions.

Filter-Based Abstractions with Correctness Guarantees for Planning under Uncertainty

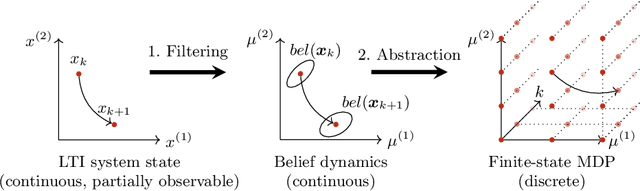
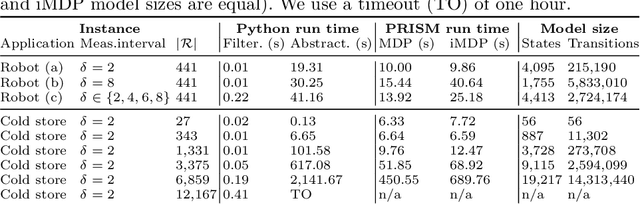
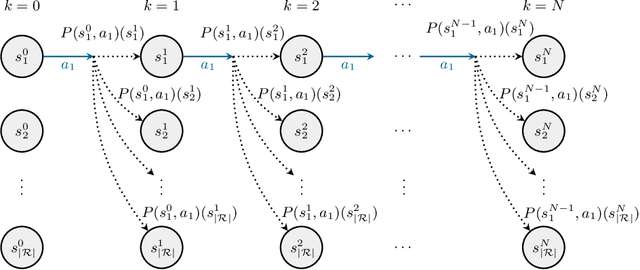
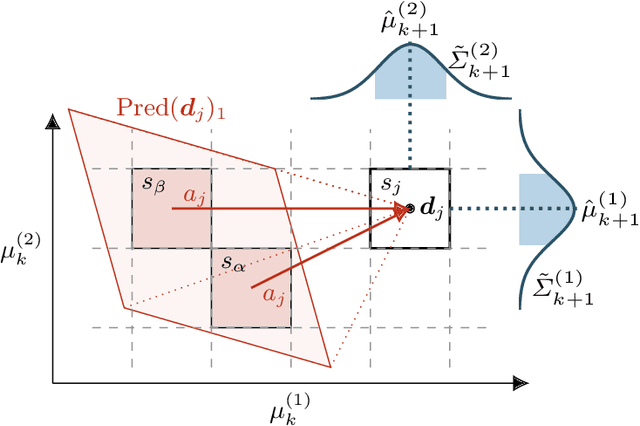
We study planning problems for continuous control systems with uncertainty caused by measurement and process noise. The goal is to find an optimal plan that guarantees that the system reaches a desired goal state within finite time. Measurement noise causes limited observability of system states, and process noise causes uncertainty in the outcome of a given plan. These factors render the problem undecidable in general. Our key contribution is a novel abstraction scheme that employs Kalman filtering as a state estimator to obtain a finite-state model, which we formalize as a Markov decision process (MDP). For this MDP, we employ state-of-the-art model checking techniques to efficiently compute plans that maximize the probability of reaching goal states. Moreover, we account for numerical imprecision in computing the abstraction by extending the MDP with intervals of probabilities as a more robust model. We show the correctness of the abstraction and provide several optimizations that aim to balance the quality of the plan and the scalability of the approach. We demonstrate that our method can handle systems that result in MDPs with thousands of states and millions of transitions.