Probabilities Are Not Enough: Formal Controller Synthesis for Stochastic Dynamical Models with Epistemic Uncertainty

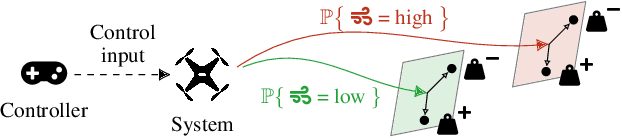
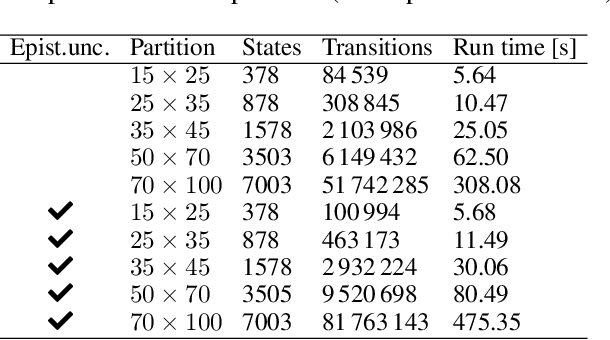
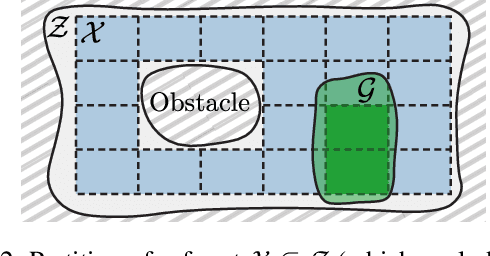
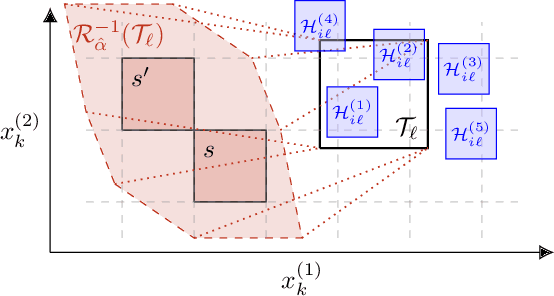
Capturing uncertainty in models of complex dynamical systems is crucial to designing safe controllers. Stochastic noise causes aleatoric uncertainty, whereas imprecise knowledge of model parameters and the presence of external disturbances lead to epistemic uncertainty. Several approaches use formal abstractions to synthesize policies that satisfy temporal specifications related to safety and reachability. However, the underlying models exclusively capture aleatoric but not epistemic uncertainty, and thus require that model parameters and disturbances are known precisely. Our contribution to overcoming this restriction is a novel abstraction-based controller synthesis method for continuous-state models with stochastic noise, uncertain parameters, and external disturbances. By sampling techniques and robust analysis, we capture both aleatoric and epistemic uncertainty, with a user-specified confidence level, in the transition probability intervals of a so-called interval Markov decision process (iMDP). We then synthesize an optimal policy on this abstract iMDP, which translates (with the specified confidence level) to a feedback controller for the continuous model, with the same performance guarantees. Our experimental benchmarks confirm that accounting for epistemic uncertainty leads to controllers that are more robust against variations in parameter values.