Tighter Value-Function Approximations for POMDPs

Solving partially observable Markov decision processes (POMDPs) typically requires reasoning about the values of exponentially many state beliefs. Towards practical performance, state-of-the-art solvers use value bounds to guide this reasoning. However, sound upper value bounds are often computationally expensive to compute, and there is a tradeoff between the tightness of such bounds and their computational cost. This paper introduces new and provably tighter upper value bounds than the commonly used fast informed bound. Our empirical evaluation shows that, despite their additional computational overhead, the new upper bounds accelerate state-of-the-art POMDP solvers on a wide range of benchmarks.

Learning-Based Verification of Stochastic Dynamical Systems with Neural Network Policies

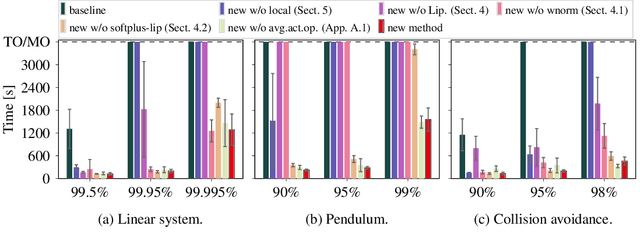
We consider the verification of neural network policies for reach-avoid control tasks in stochastic dynamical systems. We use a verification procedure that trains another neural network, which acts as a certificate proving that the policy satisfies the task. For reach-avoid tasks, it suffices to show that this certificate network is a reach-avoid supermartingale (RASM). As our main contribution, we significantly accelerate algorithmic approaches for verifying that a neural network is indeed a RASM. The main bottleneck of these approaches is the discretization of the state space of the dynamical system. The following two key contributions allow us to use a coarser discretization than existing approaches. First, we present a novel and fast method to compute tight upper bounds on Lipschitz constants of neural networks based on weighted norms. We further improve these bounds on Lipschitz constants based on the characteristics of the certificate network. Second, we integrate an efficient local refinement scheme that dynamically refines the state space discretization where necessary. Our empirical evaluation shows the effectiveness of our approach for verifying neural network policies in several benchmarks and trained with different reinforcement learning algorithms.

Approximate Dec-POMDP Solving Using Multi-Agent A*

We present an A*-based algorithm to compute policies for finite-horizon Dec-POMDPs. Our goal is to sacrifice optimality in favor of scalability for larger horizons. The main ingredients of our approach are (1) using clustered sliding window memory, (2) pruning the A* search tree, and (3) using novel A* heuristics. Our experiments show competitive performance to the state-of-the-art. Moreover, for multiple benchmarks, we achieve superior performance. In addition, we provide an A* algorithm that finds upper bounds for the optimum, tailored towards problems with long horizons. The main ingredient is a new heuristic that periodically reveals the state, thereby limiting the number of reachable beliefs. Our experiments demonstrate the efficacy and scalability of the approach.