Tighter Value-Function Approximations for POMDPs
Paper and Code
Feb 10, 2025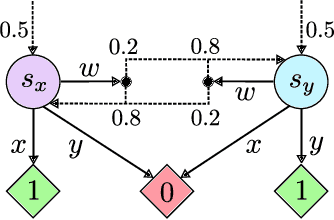

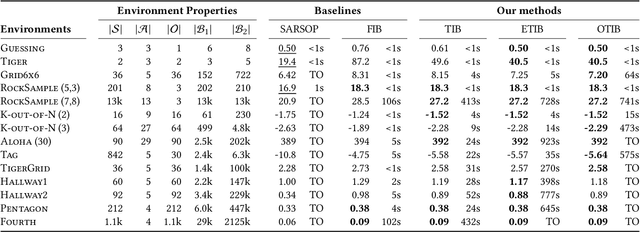
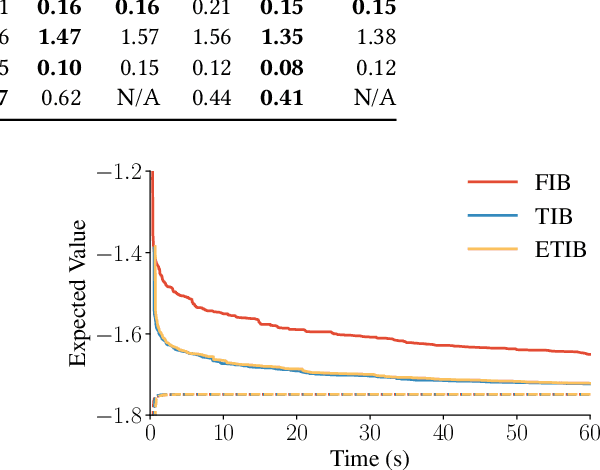
Solving partially observable Markov decision processes (POMDPs) typically requires reasoning about the values of exponentially many state beliefs. Towards practical performance, state-of-the-art solvers use value bounds to guide this reasoning. However, sound upper value bounds are often computationally expensive to compute, and there is a tradeoff between the tightness of such bounds and their computational cost. This paper introduces new and provably tighter upper value bounds than the commonly used fast informed bound. Our empirical evaluation shows that, despite their additional computational overhead, the new upper bounds accelerate state-of-the-art POMDP solvers on a wide range of benchmarks.
* AAMAS 2025 submission
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge