Tighter Value-Function Approximations for POMDPs

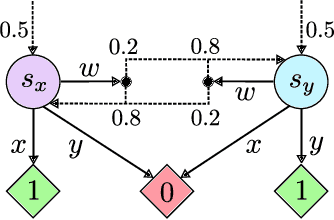
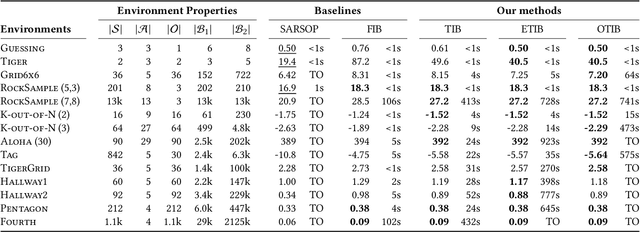
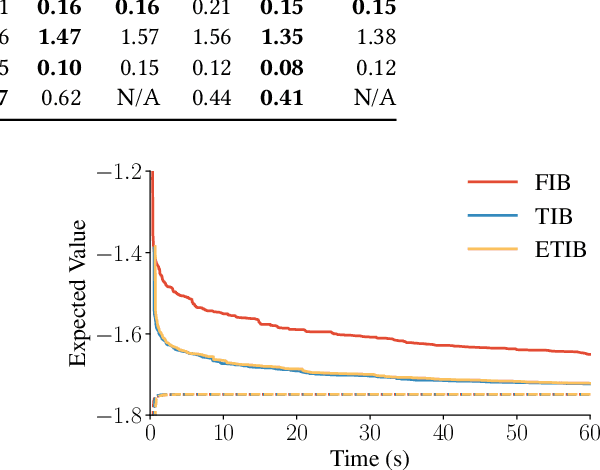
Solving partially observable Markov decision processes (POMDPs) typically requires reasoning about the values of exponentially many state beliefs. Towards practical performance, state-of-the-art solvers use value bounds to guide this reasoning. However, sound upper value bounds are often computationally expensive to compute, and there is a tradeoff between the tightness of such bounds and their computational cost. This paper introduces new and provably tighter upper value bounds than the commonly used fast informed bound. Our empirical evaluation shows that, despite their additional computational overhead, the new upper bounds accelerate state-of-the-art POMDP solvers on a wide range of benchmarks.

Robust Active Measuring under Model Uncertainty

Partial observability and uncertainty are common problems in sequential decision-making that particularly impede the use of formal models such as Markov decision processes (MDPs). However, in practice, agents may be able to employ costly sensors to measure their environment and resolve partial observability by gathering information. Moreover, imprecise transition functions can capture model uncertainty. We combine these concepts and extend MDPs to robust active-measuring MDPs (RAM-MDPs). We present an active-measure heuristic to solve RAM-MDPs efficiently and show that model uncertainty can, counterintuitively, let agents take fewer measurements. We propose a method to counteract this behavior while only incurring a bounded additional cost. We empirically compare our methods to several baselines and show their superior scalability and performance.

Act-Then-Measure: Reinforcement Learning for Partially Observable Environments with Active Measuring

We study Markov decision processes (MDPs), where agents have direct control over when and how they gather information, as formalized by action-contingent noiselessly observable MDPs (ACNO-MPDs). In these models, actions consist of two components: a control action that affects the environment, and a measurement action that affects what the agent can observe. To solve ACNO-MDPs, we introduce the act-then-measure (ATM) heuristic, which assumes that we can ignore future state uncertainty when choosing control actions. We show how following this heuristic may lead to shorter policy computation times and prove a bound on the performance loss incurred by the heuristic. To decide whether or not to take a measurement action, we introduce the concept of measuring value. We develop a reinforcement learning algorithm based on the ATM heuristic, using a Dyna-Q variant adapted for partially observable domains, and showcase its superior performance compared to prior methods on a number of partially-observable environments.