On the Detection of Markov Decision Processes
Paper and Code
Dec 23, 2021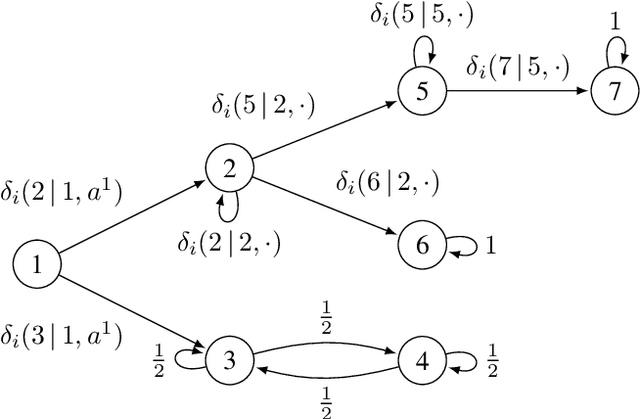
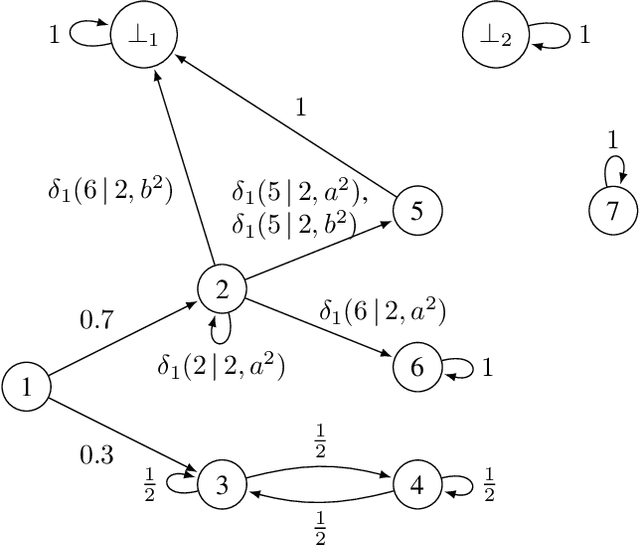
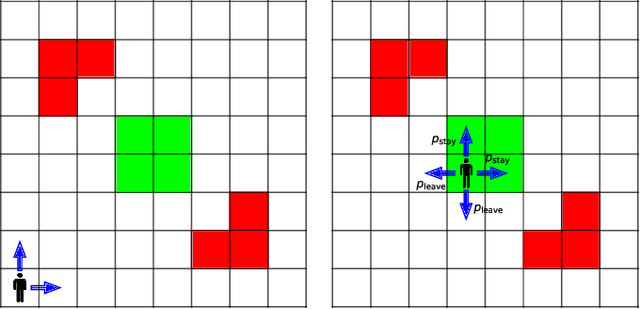
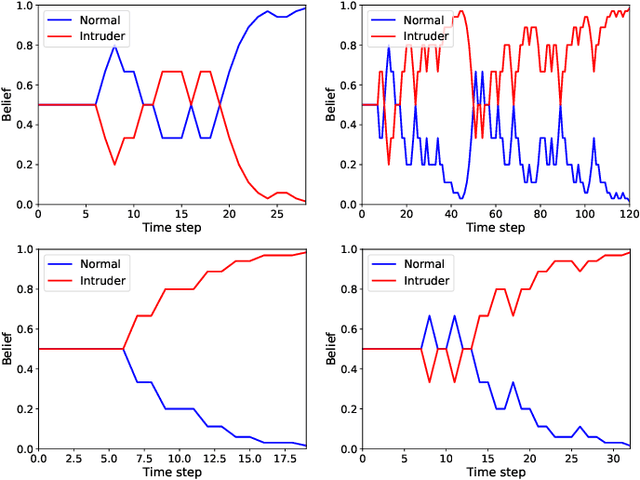
We study the detection problem for a finite set of Markov decision processes (MDPs) where the MDPs have the same state and action spaces but possibly different probabilistic transition functions. Any one of these MDPs could be the model for some underlying controlled stochastic process, but it is unknown a priori which MDP is the ground truth. We investigate whether it is possible to asymptotically detect the ground truth MDP model perfectly based on a single observed history (state-action sequence). Since the generation of histories depends on the policy adopted to control the MDPs, we discuss the existence and synthesis of policies that allow for perfect detection. We start with the case of two MDPs and establish a necessary and sufficient condition for the existence of policies that lead to perfect detection. Based on this condition, we then develop an algorithm that efficiently (in time polynomial in the size of the MDPs) determines the existence of policies and synthesizes one when they exist. We further extend the results to the more general case where there are more than two MDPs in the candidate set, and we develop a policy synthesis algorithm based on the breadth-first search and recursion. We demonstrate the effectiveness of our algorithms through numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge