Physical-Layer Security via Distributed Beamforming in the Presence of Adversaries with Unknown Locations
Paper and Code
Feb 28, 2021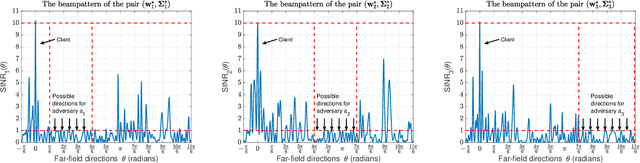
We study the problem of securely communicating a sequence of information bits with a client in the presence of multiple adversaries at unknown locations in the environment. We assume that the client and the adversaries are located in the far-field region, and all possible directions for each adversary can be expressed as a continuous interval of directions. In such a setting, we develop a periodic transmission strategy, i.e., a sequence of joint beamforming gain and artificial noise pairs, that prevents the adversaries from decreasing their uncertainty on the information sequence by eavesdropping on the transmission. We formulate a series of nonconvex semi-infinite optimization problems to synthesize the transmission strategy. We show that the semi-definite program (SDP) relaxations of these nonconvex problems are exact under an efficiently verifiable sufficient condition. We approximate the SDP relaxations, which are subject to infinitely many constraints, by randomly sampling a finite subset of the constraints and establish the probability with which optimal solutions to the obtained finite SDPs and the semi-infinite SDPs coincide. We demonstrate with numerical simulations that the proposed periodic strategy can ensure the security of communication in scenarios in which all stationary strategies fail to guarantee security.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge