Multiple Plans are Better than One: Diverse Stochastic Planning
Paper and Code
Dec 31, 2020

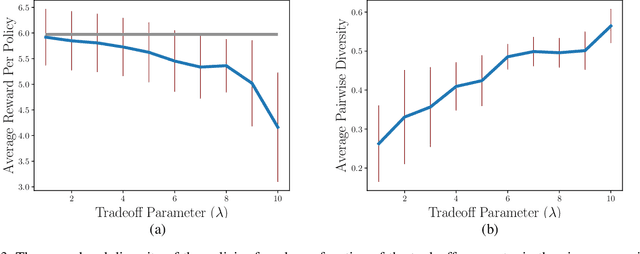
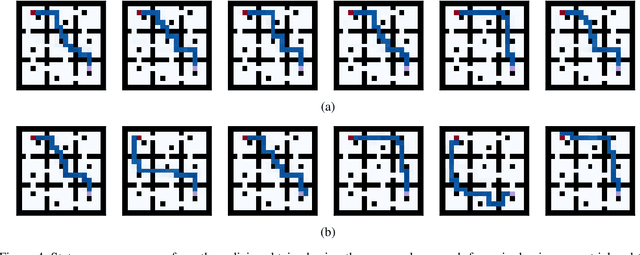
In planning problems, it is often challenging to fully model the desired specifications. In particular, in human-robot interaction, such difficulty may arise due to human's preferences that are either private or complex to model. Consequently, the resulting objective function can only partially capture the specifications and optimizing that may lead to poor performance with respect to the true specifications. Motivated by this challenge, we formulate a problem, called diverse stochastic planning, that aims to generate a set of representative -- small and diverse -- behaviors that are near-optimal with respect to the known objective. In particular, the problem aims to compute a set of diverse and near-optimal policies for systems modeled by a Markov decision process. We cast the problem as a constrained nonlinear optimization for which we propose a solution relying on the Frank-Wolfe method. We then prove that the proposed solution converges to a stationary point and demonstrate its efficacy in several planning problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge