MotionTTT: 2D Test-Time-Training Motion Estimation for 3D Motion Corrected MRI

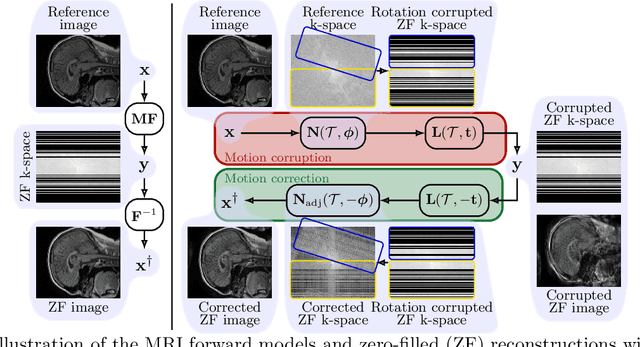
A major challenge of the long measurement times in magnetic resonance imaging (MRI), an important medical imaging technology, is that patients may move during data acquisition. This leads to severe motion artifacts in the reconstructed images and volumes. In this paper, we propose a deep learning-based test-time-training method for accurate motion estimation. The key idea is that a neural network trained for motion-free reconstruction has a small loss if there is no motion, thus optimizing over motion parameters passed through the reconstruction network enables accurate estimation of motion. The estimated motion parameters enable to correct for the motion and to reconstruct accurate motion-corrected images. Our method uses 2D reconstruction networks to estimate rigid motion in 3D, and constitutes the first deep learning based method for 3D rigid motion estimation towards 3D-motion-corrected MRI. We show that our method can provably reconstruct motion parameters for a simple signal and neural network model. We demonstrate the effectiveness of our method for both retrospectively simulated motion and prospectively collected real motion-corrupted data.

Analyzing the Sample Complexity of Self-Supervised Image Reconstruction Methods

Supervised training of deep neural networks on pairs of clean image and noisy measurement achieves state-of-the-art performance for many image reconstruction tasks, but such training pairs are usually difficult to collect. A variety of self-supervised methods enable training based on noisy measurements only, without clean images. In this work, we investigate the cost of self-supervised training by characterizing its sample complexity. We focus on a class of self-supervised methods that enable the computation of unbiased estimates of gradients of the supervised loss, including noise2noise methods. We first analytically show that a model trained with such self-supervised training is as good as the same model trained in a supervised fashion, but self-supervised training requires more examples than supervised training. We then study self-supervised denoising and accelerated MRI empirically and characterize the cost of self-supervised training in terms of the number of additional samples required, and find that the performance gap between self-supervised and supervised training vanishes as a function of the training examples, at a problem-dependent rate, as predicted by our theory.

Scaling Laws For Deep Learning Based Image Reconstruction

Deep neural networks trained end-to-end to map a measurement of a (noisy) image to a clean image perform excellent for a variety of linear inverse problems. Current methods are only trained on a few hundreds or thousands of images as opposed to the millions of examples deep networks are trained on in other domains. In this work, we study whether major performance gains are expected from scaling up the training set size. We consider image denoising, accelerated magnetic resonance imaging, and super-resolution and empirically determine the reconstruction quality as a function of training set size, while optimally scaling the network size. For all three tasks we find that an initially steep power-law scaling slows significantly already at moderate training set sizes. Interpolating those scaling laws suggests that even training on millions of images would not significantly improve performance. To understand the expected behavior, we analytically characterize the performance of a linear estimator learned with early stopped gradient descent. The result formalizes the intuition that once the error induced by learning the signal model is small relative to the error floor, more training examples do not improve performance.