Resolution-Robust 3D MRI Reconstruction with 2D Diffusion Priors: Diverse-Resolution Training Outperforms Interpolation

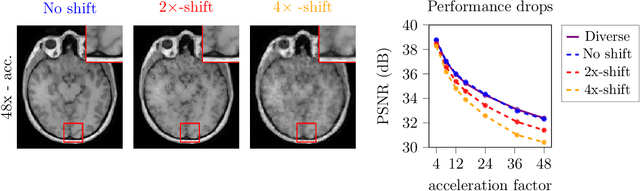
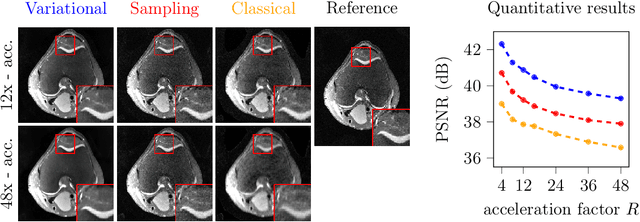
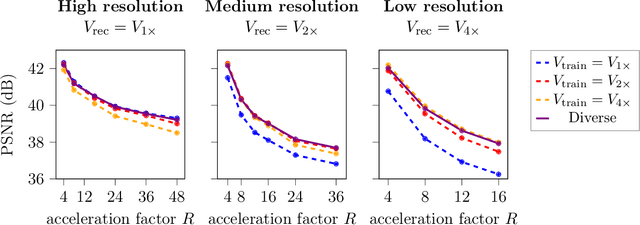
Deep learning-based 3D imaging, in particular magnetic resonance imaging (MRI), is challenging because of limited availability of 3D training data. Therefore, 2D diffusion models trained on 2D slices are starting to be leveraged for 3D MRI reconstruction. However, as we show in this paper, existing methods pertain to a fixed voxel size, and performance degrades when the voxel size is varied, as it is often the case in clinical practice. In this paper, we propose and study several approaches for resolution-robust 3D MRI reconstruction with 2D diffusion priors. As a result of this investigation, we obtain a simple resolution-robust variational 3D reconstruction approach based on diffusion-guided regularization of randomly sampled 2D slices. This method provides competitive reconstruction quality compared to posterior sampling baselines. Towards resolving the sensitivity to resolution-shifts, we investigate state-of-the-art model-based approaches including Gaussian splatting, neural representations, and infinite-dimensional diffusion models, as well as a simple data-centric approach of training the diffusion model on several resolutions. Our experiments demonstrate that the model-based approaches fail to close the performance gap in 3D MRI. In contrast, the data-centric approach of training the diffusion model on various resolutions effectively provides a resolution-robust method without compromising accuracy.

Learning Provably Robust Estimators for Inverse Problems via Jittering

Deep neural networks provide excellent performance for inverse problems such as denoising. However, neural networks can be sensitive to adversarial or worst-case perturbations. This raises the question of whether such networks can be trained efficiently to be worst-case robust. In this paper, we investigate whether jittering, a simple regularization technique that adds isotropic Gaussian noise during training, is effective for learning worst-case robust estimators for inverse problems. While well studied for prediction in classification tasks, the effectiveness of jittering for inverse problems has not been systematically investigated. In this paper, we present a novel analytical characterization of the optimal $\ell_2$-worst-case robust estimator for linear denoising and show that jittering yields optimal robust denoisers. Furthermore, we examine jittering empirically via training deep neural networks (U-nets) for natural image denoising, deconvolution, and accelerated magnetic resonance imaging (MRI). The results show that jittering significantly enhances the worst-case robustness, but can be suboptimal for inverse problems beyond denoising. Moreover, our results imply that training on real data which often contains slight noise is somewhat robustness enhancing.