High-Dimensional Confidence Regions in Sparse MRI
Paper and Code
Jul 18, 2024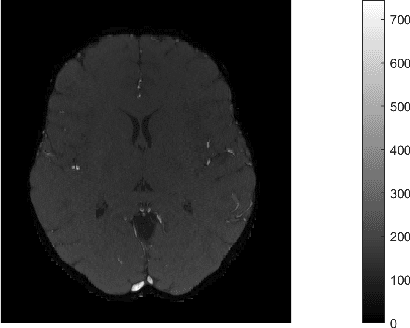
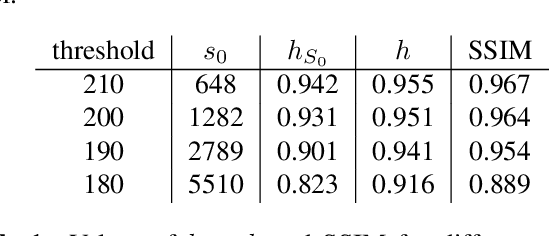
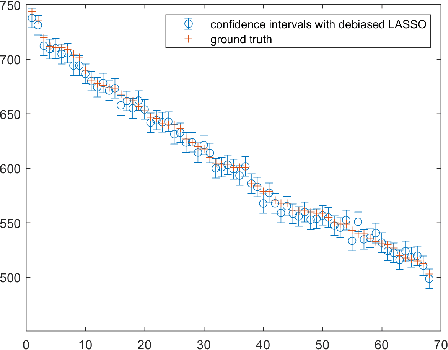
One of the most promising solutions for uncertainty quantification in high-dimensional statistics is the debiased LASSO that relies on unconstrained $\ell_1$-minimization. The initial works focused on real Gaussian designs as a toy model for this problem. However, in medical imaging applications, such as compressive sensing for MRI, the measurement system is represented by a (subsampled) complex Fourier matrix. The purpose of this work is to extend the method to the MRI case in order to construct confidence intervals for each pixel of an MR image. We show that a sufficient amount of data is $n \gtrsim \max\{ s_0\log^2 s_0\log p, s_0 \log^2 p \}$.
* Recognized with Best Student Paper Award at ICASSP 2023. arXiv admin
note: substantial text overlap with arXiv:2212.14864
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge