Inference-Time Reward Hacking in Large Language Models

A common paradigm to improve the performance of large language models is optimizing for a reward model. Reward models assign a numerical score to LLM outputs indicating, for example, which response would likely be preferred by a user or is most aligned with safety goals. However, reward models are never perfect. They inevitably function as proxies for complex desiderata such as correctness, helpfulness, and safety. By overoptimizing for a misspecified reward, we can subvert intended alignment goals and reduce overall performance -- a phenomenon commonly referred to as reward hacking. In this work, we characterize reward hacking in inference-time alignment and demonstrate when and how we can mitigate it by hedging on the proxy reward. We study this phenomenon under Best-of-$n$ (BoN) and Soft-Best-of-$n$ (SBoN), and we introduce Best-of-Poisson (BoP) that provides an efficient, near-exact approximation of the optimal reward-KL divergence policy at inference time. We show that the characteristic pattern of hacking as observed in practice (where the true reward first increases before declining) is an inevitable property of a broad class of inference-time mechanisms, including BoN and BoP. To counter this effect, hedging offers a tactical choice to avoid placing undue confidence in high but potentially misleading proxy reward signals. We introduce HedgeTune, an efficient algorithm to find the optimal inference-time parameter and avoid reward hacking. We demonstrate through experiments that hedging mitigates reward hacking and achieves superior distortion-reward tradeoffs with minimal computational overhead.

Rigor in AI: Doing Rigorous AI Work Requires a Broader, Responsible AI-Informed Conception of Rigor

In AI research and practice, rigor remains largely understood in terms of methodological rigor -- such as whether mathematical, statistical, or computational methods are correctly applied. We argue that this narrow conception of rigor has contributed to the concerns raised by the responsible AI community, including overblown claims about AI capabilities. Our position is that a broader conception of what rigorous AI research and practice should entail is needed. We believe such a conception -- in addition to a more expansive understanding of (1) methodological rigor -- should include aspects related to (2) what background knowledge informs what to work on (epistemic rigor); (3) how disciplinary, community, or personal norms, standards, or beliefs influence the work (normative rigor); (4) how clearly articulated the theoretical constructs under use are (conceptual rigor); (5) what is reported and how (reporting rigor); and (6) how well-supported the inferences from existing evidence are (interpretative rigor). In doing so, we also aim to provide useful language and a framework for much-needed dialogue about the AI community's work by researchers, policymakers, journalists, and other stakeholders.

Attack-Aware Noise Calibration for Differential Privacy

Differential privacy (DP) is a widely used approach for mitigating privacy risks when training machine learning models on sensitive data. DP mechanisms add noise during training to limit the risk of information leakage. The scale of the added noise is critical, as it determines the trade-off between privacy and utility. The standard practice is to select the noise scale in terms of a privacy budget parameter $\epsilon$. This parameter is in turn interpreted in terms of operational attack risk, such as accuracy, or sensitivity and specificity of inference attacks against the privacy of the data. We demonstrate that this two-step procedure of first calibrating the noise scale to a privacy budget $\epsilon$, and then translating $\epsilon$ to attack risk leads to overly conservative risk assessments and unnecessarily low utility. We propose methods to directly calibrate the noise scale to a desired attack risk level, bypassing the intermediate step of choosing $\epsilon$. For a target attack risk, our approach significantly decreases noise scale, leading to increased utility at the same level of privacy. We empirically demonstrate that calibrating noise to attack sensitivity/specificity, rather than $\epsilon$, when training privacy-preserving ML models substantially improves model accuracy for the same risk level. Our work provides a principled and practical way to improve the utility of privacy-preserving ML without compromising on privacy.

Predictive Churn with the Set of Good Models

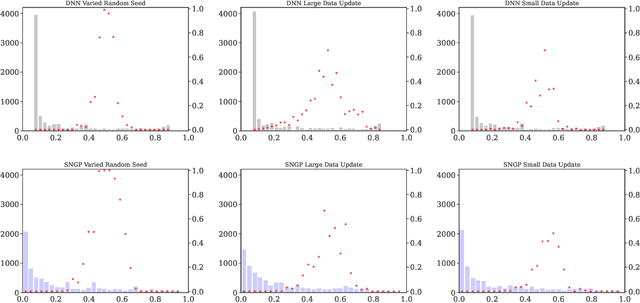
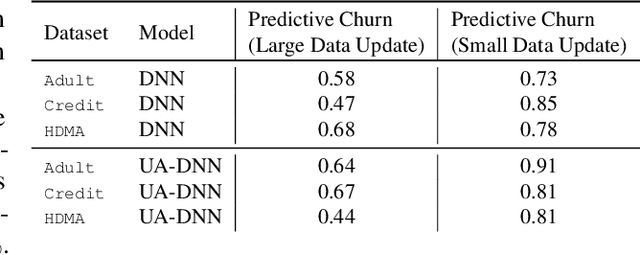
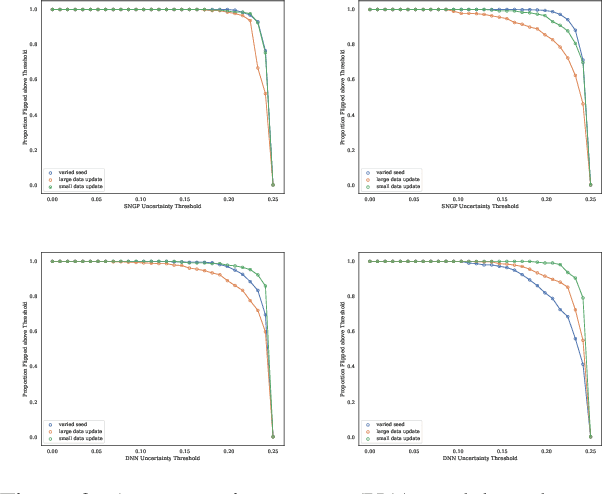
Machine learning models in modern mass-market applications are often updated over time. One of the foremost challenges faced is that, despite increasing overall performance, these updates may flip specific model predictions in unpredictable ways. In practice, researchers quantify the number of unstable predictions between models pre and post update -- i.e., predictive churn. In this paper, we study this effect through the lens of predictive multiplicity -- i.e., the prevalence of conflicting predictions over the set of near-optimal models (the Rashomon set). We show how traditional measures of predictive multiplicity can be used to examine expected churn over this set of prospective models -- i.e., the set of models that may be used to replace a baseline model in deployment. We present theoretical results on the expected churn between models within the Rashomon set from different perspectives. And we characterize expected churn over model updates via the Rashomon set, pairing our analysis with empirical results on real-world datasets -- showing how our approach can be used to better anticipate, reduce, and avoid churn in consumer-facing applications. Further, we show that our approach is useful even for models enhanced with uncertainty awareness.

Rashomon Capacity: A Metric for Predictive Multiplicity in Probabilistic Classification

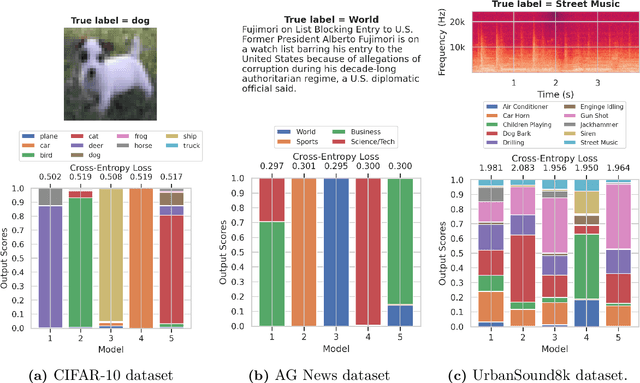
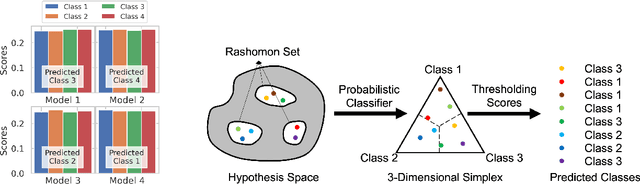
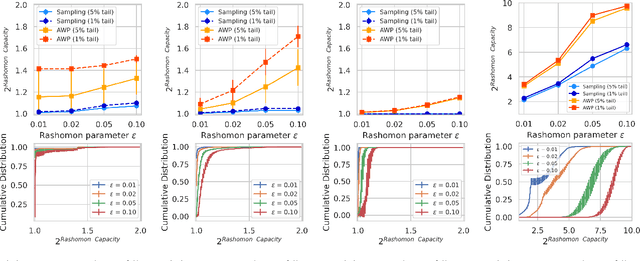
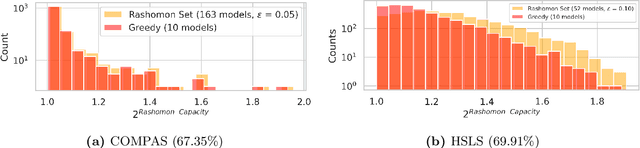
Predictive multiplicity occurs when classification models with nearly indistinguishable average performances assign conflicting predictions to individual samples. When used for decision-making in applications of consequence (e.g., lending, education, criminal justice), models developed without regard for predictive multiplicity may result in unjustified and arbitrary decisions for specific individuals. We introduce a new measure of predictive multiplicity in probabilistic classification called Rashomon Capacity. Prior metrics for predictive multiplicity focus on classifiers that output thresholded (i.e., 0-1) predicted classes. In contrast, Rashomon Capacity applies to probabilistic classifiers, capturing more nuanced score variations for individual samples. We provide a rigorous derivation for Rashomon Capacity, argue its intuitive appeal, and demonstrate how to estimate it in practice. We show that Rashomon Capacity yields principled strategies for disclosing conflicting models to stakeholders. Our numerical experiments illustrate how Rashomon Capacity captures predictive multiplicity in various datasets and learning models, including neural networks. The tools introduced in this paper can help data scientists measure, report, and ultimately resolve predictive multiplicity prior to model deployment.

Obfuscation via Information Density Estimation

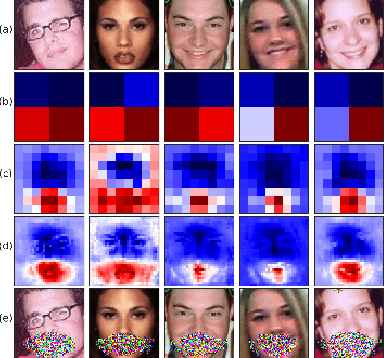
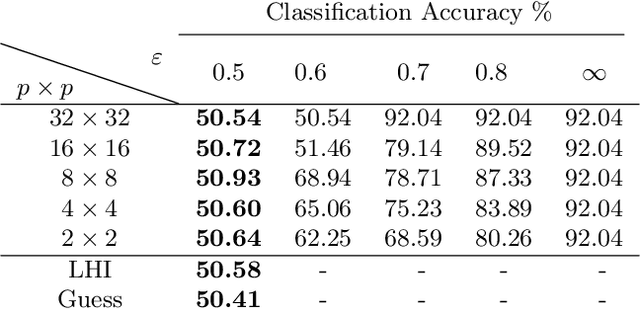
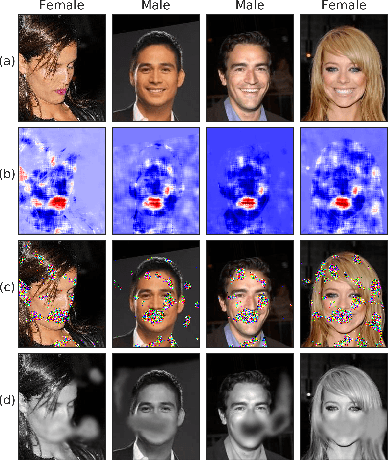
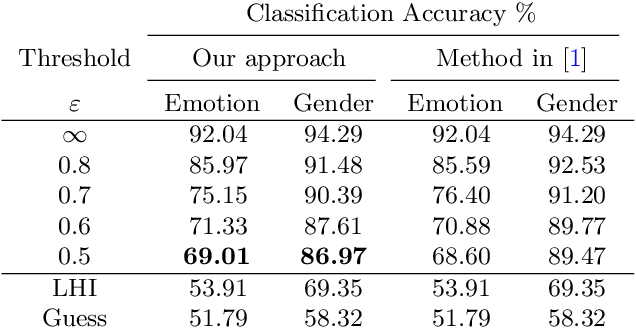
Identifying features that leak information about sensitive attributes is a key challenge in the design of information obfuscation mechanisms. In this paper, we propose a framework to identify information-leaking features via information density estimation. Here, features whose information densities exceed a pre-defined threshold are deemed information-leaking features. Once these features are identified, we sequentially pass them through a targeted obfuscation mechanism with a provable leakage guarantee in terms of $\mathsf{E}_\gamma$-divergence. The core of this mechanism relies on a data-driven estimate of the trimmed information density for which we propose a novel estimator, named the trimmed information density estimator (TIDE). We then use TIDE to implement our mechanism on three real-world datasets. Our approach can be used as a data-driven pipeline for designing obfuscation mechanisms targeting specific features.

Predictive Multiplicity in Classification

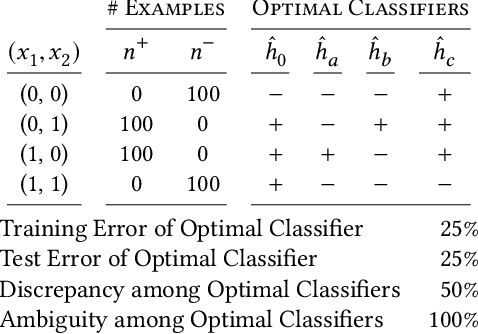
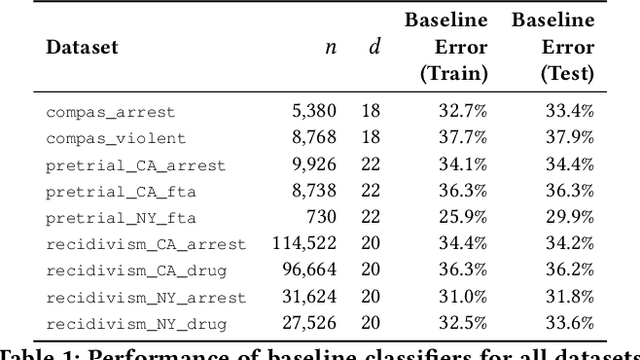
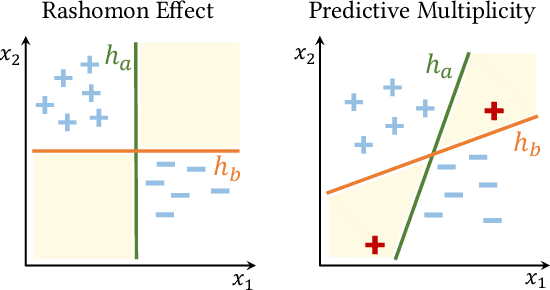
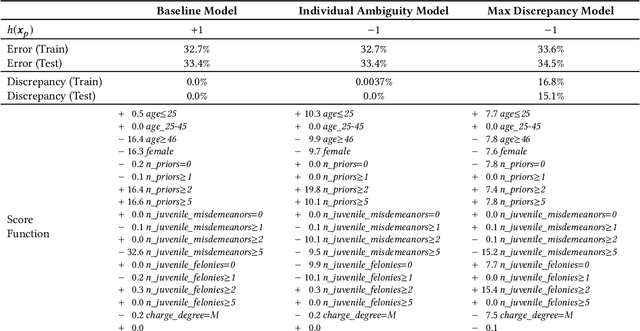
In the context of machine learning, a prediction problem exhibits predictive multiplicity if there exist several "good" models that attain identical or near-identical performance (i.e., accuracy, AUC, etc.). In this paper, we study the effects of multiplicity in human-facing applications, such as credit scoring and recidivism prediction. We introduce a specific notion of multiplicity -- predictive multiplicity -- to describe the existence of good models that output conflicting predictions. Unlike existing notions of multiplicity (e.g., the Rashomon effect), predictive multiplicity reflects irreconcilable differences in the predictions of models with comparable performance, and presents new challenges for common practices such as model selection and local explanation. We propose measures to evaluate the predictive multiplicity in classification problems. We present integer programming methods to compute these measures for a given datasets by solving empirical risk minimization problems with discrete constraints. We demonstrate how these tools can inform stakeholders on a large collection of recidivism prediction problems. Our results show that real-world prediction problems often admit many good models that output wildly conflicting predictions, and support the need to report predictive multiplicity in model development.

Optimized Score Transformation for Fair Classification

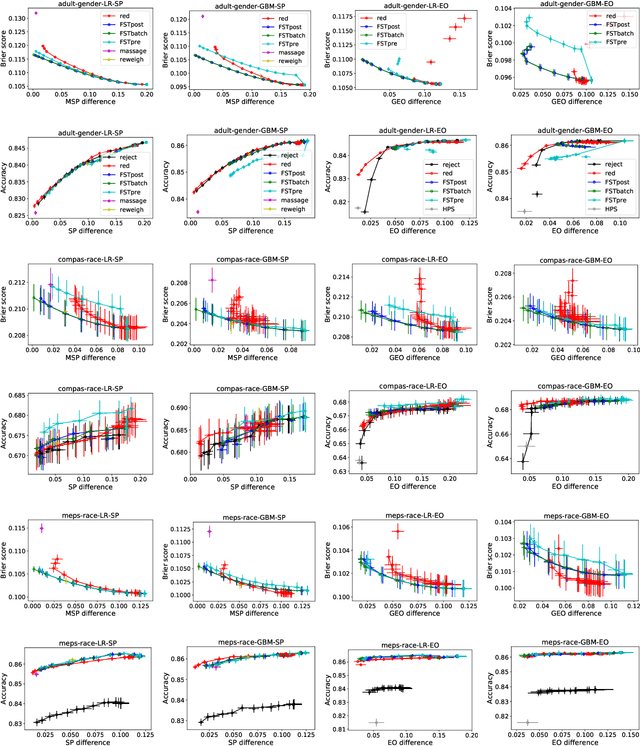
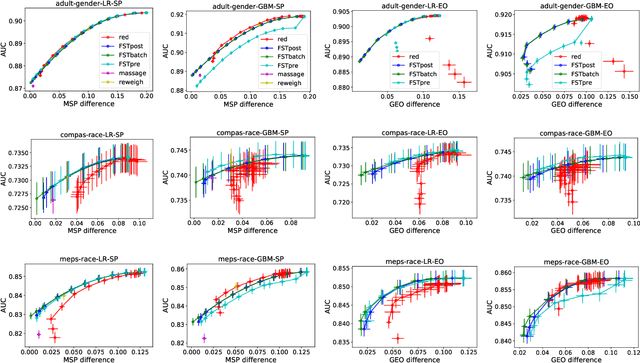
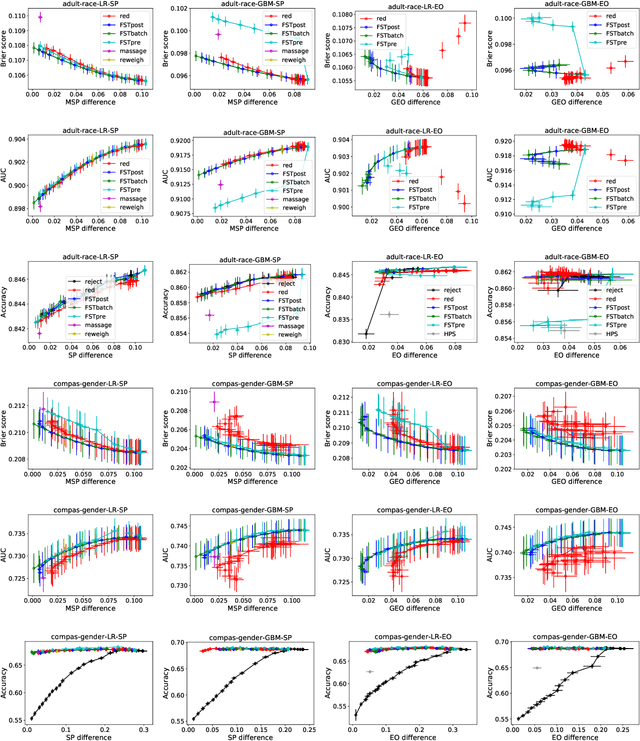
This paper considers fair probabilistic classification where the outputs of primary interest are predicted probabilities, commonly referred to as scores. We formulate the problem of transforming scores to satisfy fairness constraints that are linear in conditional means of scores while minimizing the loss in utility. The same formulation can be applied both to post-process classifier outputs as well as to pre-process training data. We derive a closed-form expression for the optimal transformed scores and a convex optimization problem for the transformation parameters. In the population limit, the transformed score function is the fairness-constrained minimizer of cross-entropy with respect to the optimal unconstrained scores. In the finite sample setting, we propose to approach this solution using a combination of standard probabilistic classifiers and ADMM. Comprehensive experiments show that the proposed \mname has advantages for score-based metrics such as Brier score and AUC while remaining competitive for binary label-based metrics such as accuracy.