Predictive Multiplicity in Classification
Paper and Code
Sep 14, 2019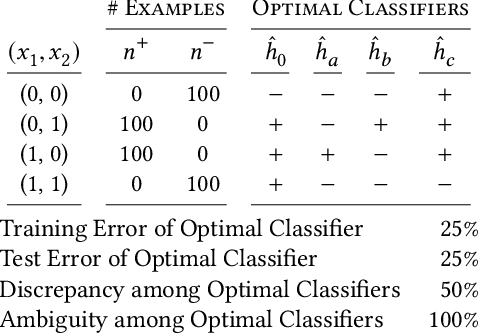
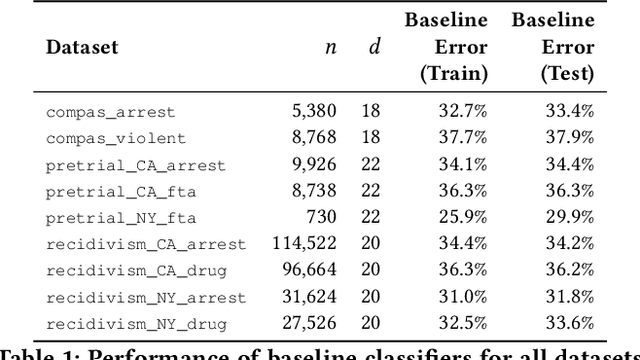
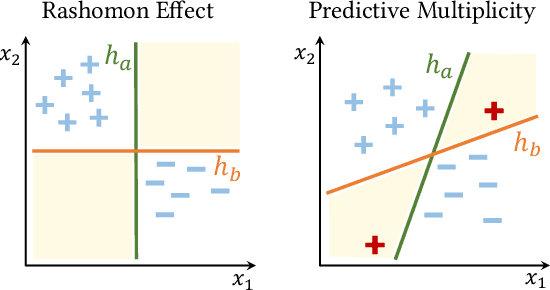
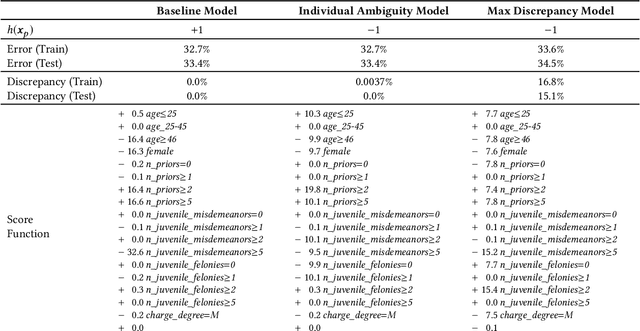
In the context of machine learning, a prediction problem exhibits predictive multiplicity if there exist several "good" models that attain identical or near-identical performance (i.e., accuracy, AUC, etc.). In this paper, we study the effects of multiplicity in human-facing applications, such as credit scoring and recidivism prediction. We introduce a specific notion of multiplicity -- predictive multiplicity -- to describe the existence of good models that output conflicting predictions. Unlike existing notions of multiplicity (e.g., the Rashomon effect), predictive multiplicity reflects irreconcilable differences in the predictions of models with comparable performance, and presents new challenges for common practices such as model selection and local explanation. We propose measures to evaluate the predictive multiplicity in classification problems. We present integer programming methods to compute these measures for a given datasets by solving empirical risk minimization problems with discrete constraints. We demonstrate how these tools can inform stakeholders on a large collection of recidivism prediction problems. Our results show that real-world prediction problems often admit many good models that output wildly conflicting predictions, and support the need to report predictive multiplicity in model development.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge