Optimized Score Transformation for Fair Classification

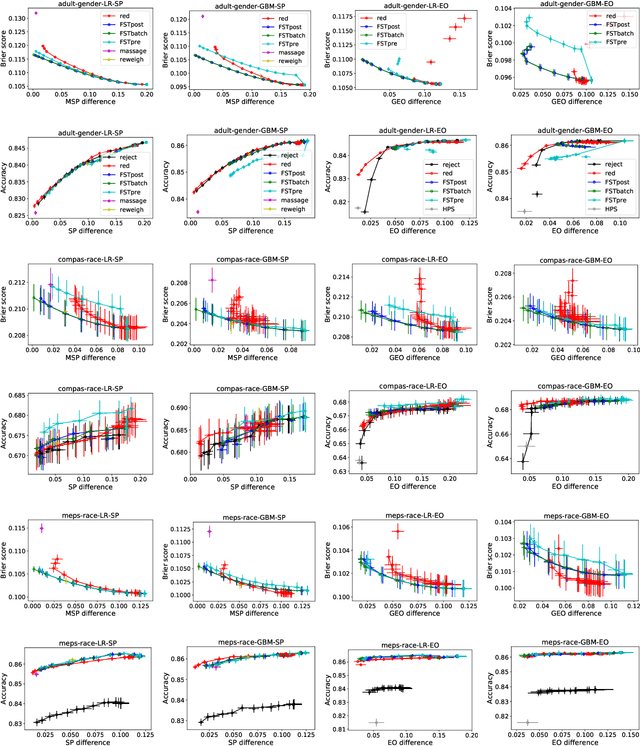
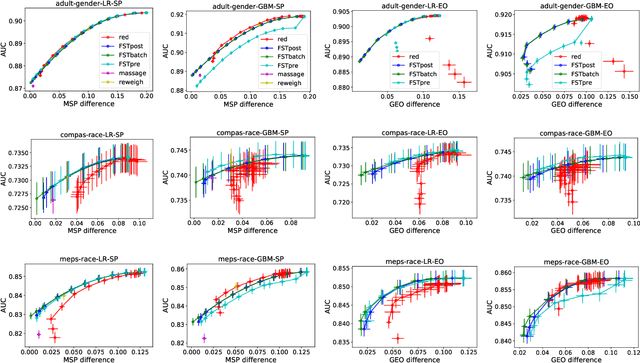
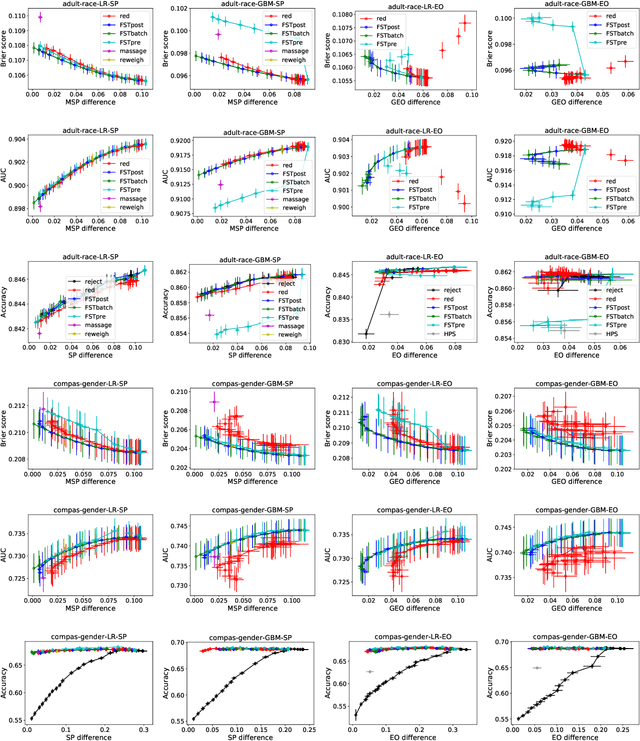
This paper considers fair probabilistic classification where the outputs of primary interest are predicted probabilities, commonly referred to as scores. We formulate the problem of transforming scores to satisfy fairness constraints that are linear in conditional means of scores while minimizing the loss in utility. The same formulation can be applied both to post-process classifier outputs as well as to pre-process training data. We derive a closed-form expression for the optimal transformed scores and a convex optimization problem for the transformation parameters. In the population limit, the transformed score function is the fairness-constrained minimizer of cross-entropy with respect to the optimal unconstrained scores. In the finite sample setting, we propose to approach this solution using a combination of standard probabilistic classifiers and ADMM. Comprehensive experiments show that the proposed \mname has advantages for score-based metrics such as Brier score and AUC while remaining competitive for binary label-based metrics such as accuracy.