Joshua K. Behne
Rank-one matrix estimation with groupwise heteroskedasticity
Jun 22, 2021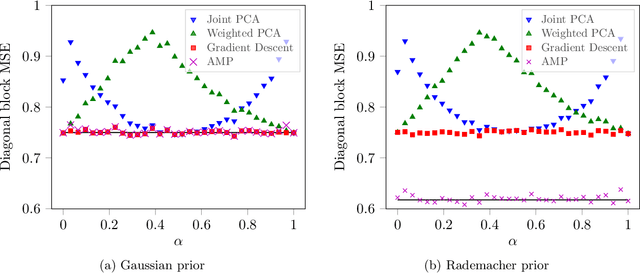
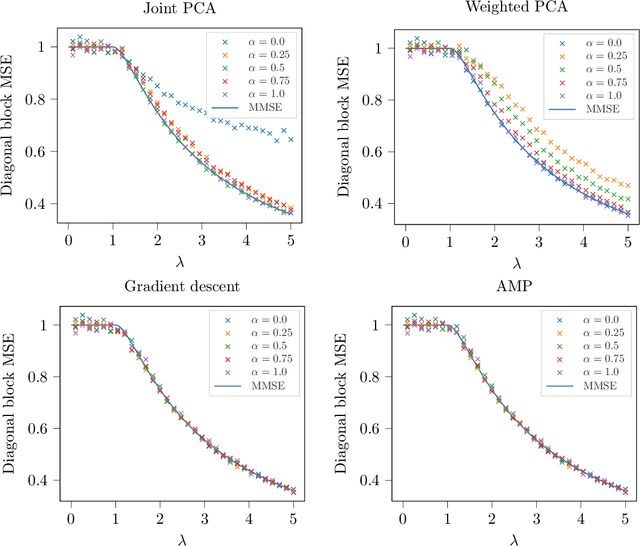
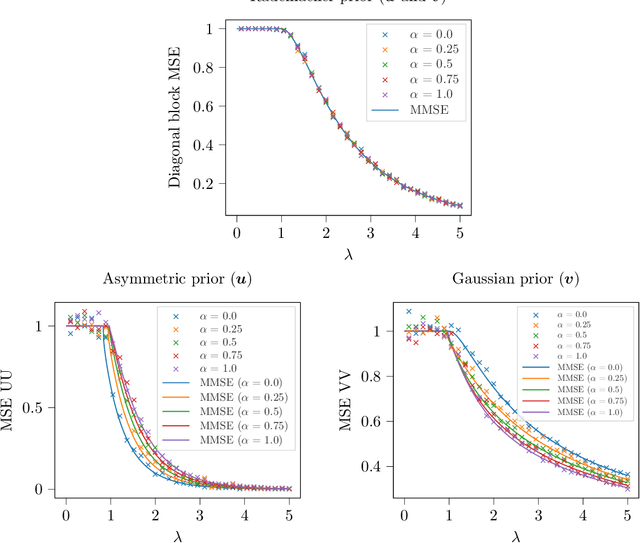
Abstract:We study the problem of estimating a rank-one matrix from Gaussian observations where different blocks of the matrix are observed under different noise levels. This problem is motivated by applications in clustering and community detection where latent variables can be partitioned into a fixed number of known groups (e.g., users and items) and the blocks of the matrix correspond to different types of pairwise interactions (e.g., user-user, user-item, or item-item interactions). In the setting where the number of blocks is fixed while the number of variables tends to infinity, we prove asymptotically exact formulas for the minimum mean-squared error in estimating both the matrix and the latent variables. These formulas describe the weak recovery thresholds for the problem and reveal invariance properties with respect to certain scalings of the noise variance. We also derive an approximate message passing algorithm and a gradient descent algorithm and show empirically that these algorithms achieve the information-theoretic limits in certain regimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge