SPICE: Submodular Penalized Information-Conflict Selection for Efficient Large Language Model Training

Information-based data selection for instruction tuning is compelling: maximizing the log-determinant of the Fisher information yields a monotone submodular objective, enabling greedy algorithms to achieve a $(1-1/e)$ approximation under a cardinality budget. In practice, however, we identify alleviating gradient conflicts, misalignment between per-sample gradients, is a key factor that slows down the decay of marginal log-determinant information gains, thereby preventing significant loss of information. We formalize this via an $\varepsilon$-decomposition that quantifies the deviation from ideal submodularity as a function of conflict statistics, yielding data-dependent approximation factors that tighten as conflicts diminish. Guided by this analysis, we propose SPICE, a conflict-aware selector that maximizes information while penalizing misalignment, and that supports early stopping and proxy models for efficiency. Empirically, SPICE selects subsets with higher log-determinant information than original criteria, and these informational gains translate into performance improvements: across 8 benchmarks with LLaMA2-7B and Qwen2-7B, SPICE uses only 10% of the data, yet matches or exceeds 6 methods including full-data tuning. This achieves performance improvements with substantially lower training cost.

Identification of mental fatigue in language comprehension tasks based on EEG and deep learning

Mental fatigue increases the risk of operator error in language comprehension tasks. In order to prevent operator performance degradation, we used EEG signals to assess the mental fatigue of operators in human-computer systems. This study presents an experimental design for fatigue detection in language comprehension tasks. We obtained EEG signals from a 14-channel wireless EEG detector in 15 healthy participants. Each participant was given a cognitive test of a language comprehension task, in the form of multiple choice questions, in which pronoun references were selected between nominal and surrogate sentences. In this paper, the 2400 EEG fragments collected are divided into three data sets according to different utilization rates, namely 1200s data set with 50% utilization rate, 1500s data set with 62.5% utilization rate, and 1800s data set with 75% utilization rate. In the aspect of feature extraction, different EEG features were extracted, including time domain features, frequency domain features and entropy features, and the effects of different features and feature combinations on classification accuracy were explored. In terms of classification, we introduced the Convolutional Neural Network (CNN) method as the preferred method, It was compared with Least Squares Support Vector Machines(LSSVM),Support Vector Machines(SVM),Logistic Regression (LR), Random Forest(RF), Naive Bayes (NB), K-Nearest Neighbor (KNN) and Decision Tree(DT).According to the results, the classification accuracy of convolutional neural network (CNN) is higher than that of other classification methods. The classification results show that the classification accuracy of 1200S dataset is higher than the other two datasets. The combination of Frequency and entropy feature and CNN has the highest classification accuracy, which is 85.34%.

Convergence of Gaussian-smoothed optimal transport distance with sub-gamma distributions and dependent samples

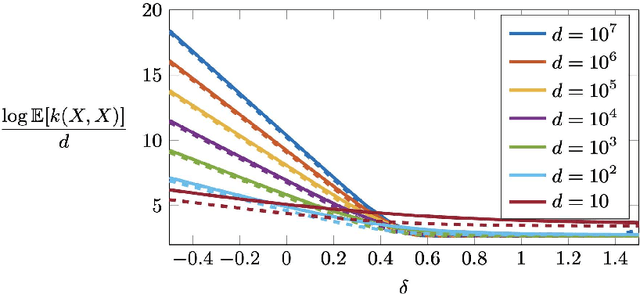
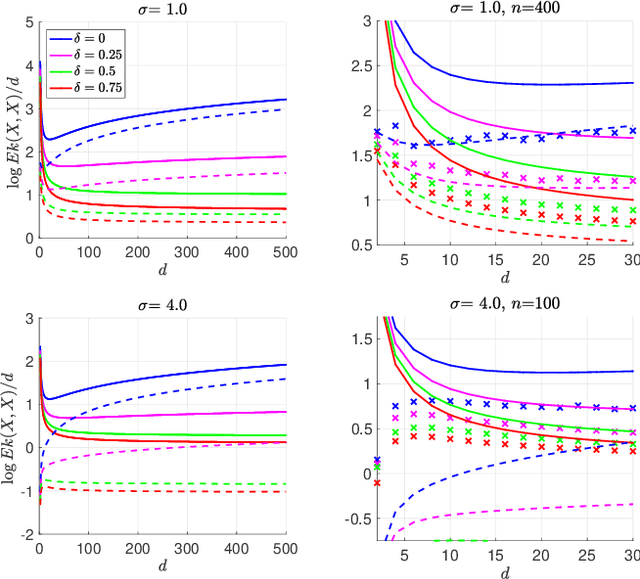
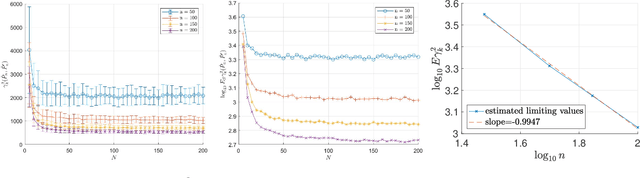
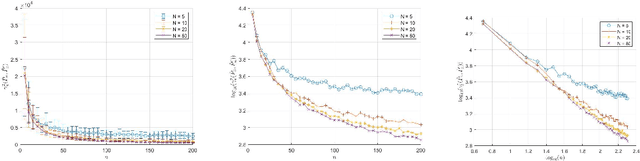
The Gaussian-smoothed optimal transport (GOT) framework, recently proposed by Goldfeld et al., scales to high dimensions in estimation and provides an alternative to entropy regularization. This paper provides convergence guarantees for estimating the GOT distance under more general settings. For the Gaussian-smoothed $p$-Wasserstein distance in $d$ dimensions, our results require only the existence of a moment greater than $d + 2p$. For the special case of sub-gamma distributions, we quantify the dependence on the dimension $d$ and establish a phase transition with respect to the scale parameter. We also prove convergence for dependent samples, only requiring a condition on the pairwise dependence of the samples measured by the covariance of the feature map of a kernel space. A key step in our analysis is to show that the GOT distance is dominated by a family of kernel maximum mean discrepancy (MMD) distances with a kernel that depends on the cost function as well as the amount of Gaussian smoothing. This insight provides further interpretability for the GOT framework and also introduces a class of kernel MMD distances with desirable properties. The theoretical results are supported by numerical experiments.