Screening for Sparse Online Learning
Paper and Code
Jan 18, 2021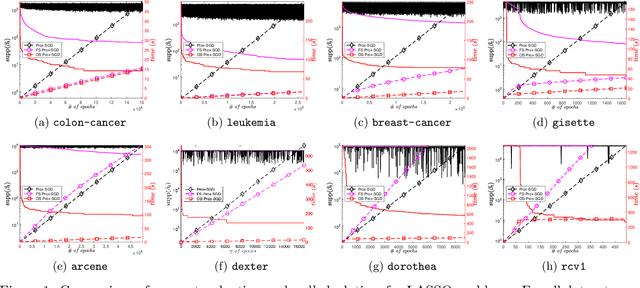
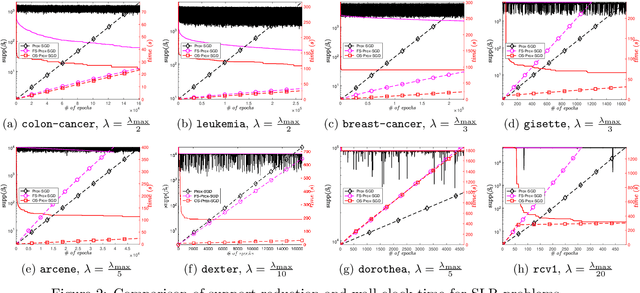
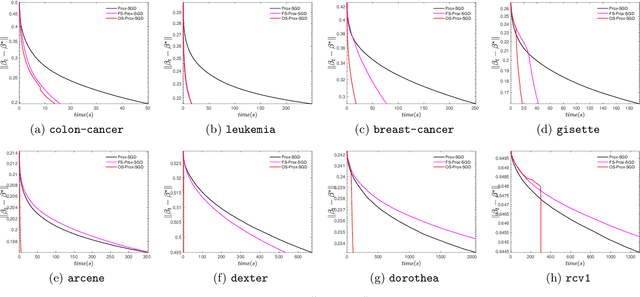
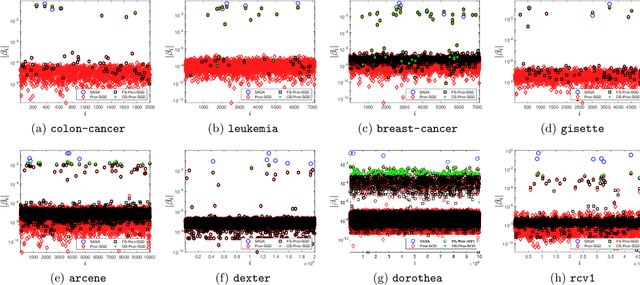
Sparsity promoting regularizers are widely used to impose low-complexity structure (e.g. l1-norm for sparsity) to the regression coefficients of supervised learning. In the realm of deterministic optimization, the sequence generated by iterative algorithms (such as proximal gradient descent) exhibit "finite activity identification", namely, they can identify the low-complexity structure in a finite number of iterations. However, most online algorithms (such as proximal stochastic gradient descent) do not have the property owing to the vanishing step-size and non-vanishing variance. In this paper, by combining with a screening rule, we show how to eliminate useless features of the iterates generated by online algorithms, and thereby enforce finite activity identification. One consequence is that when combined with any convergent online algorithm, sparsity properties imposed by the regularizer can be exploited for computational gains. Numerically, significant acceleration can be obtained.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge