A Guide to Stochastic Optimisation for Large-Scale Inverse Problems

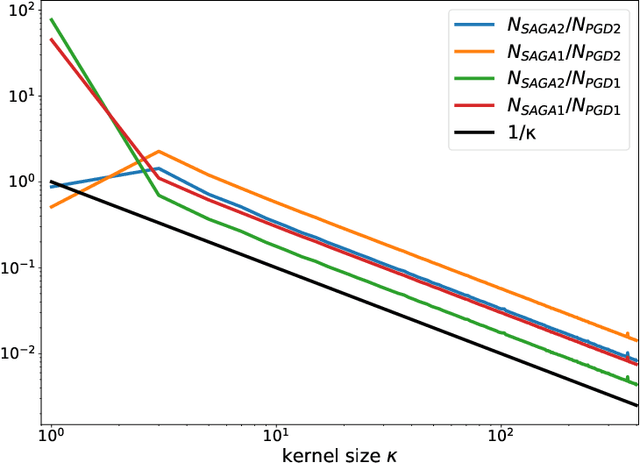
Stochastic optimisation algorithms are the de facto standard for machine learning with large amounts of data. Handling only a subset of available data in each optimisation step dramatically reduces the per-iteration computational costs, while still ensuring significant progress towards the solution. Driven by the need to solve large-scale optimisation problems as efficiently as possible, the last decade has witnessed an explosion of research in this area. Leveraging the parallels between machine learning and inverse problems has allowed harnessing the power of this research wave for solving inverse problems. In this survey, we provide a comprehensive account of the state-of-the-art in stochastic optimisation from the viewpoint of inverse problems. We present algorithms with diverse modalities of problem randomisation and discuss the roles of variance reduction, acceleration, higher-order methods, and other algorithmic modifications, and compare theoretical results with practical behaviour. We focus on the potential and the challenges for stochastic optimisation that are unique to inverse imaging problems and are not commonly encountered in machine learning. We conclude the survey with illustrative examples from imaging problems to examine the advantages and disadvantages that this new generation of algorithms bring to the field of inverse problems.

Graph Neural Network for Local Corruption Recovery

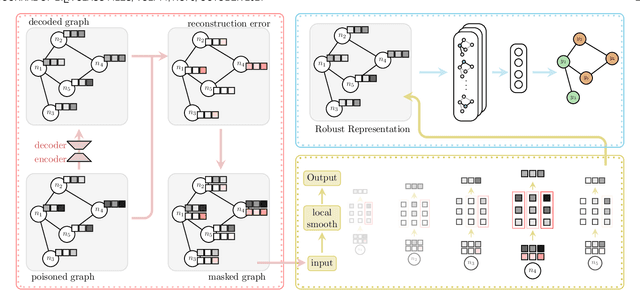
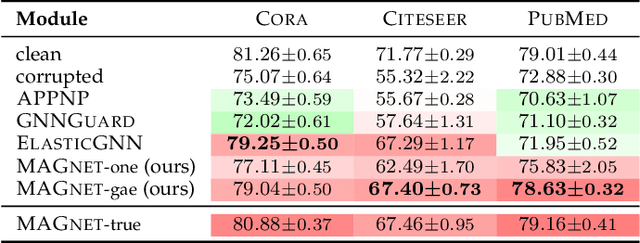
Graph neural networks (GNNs) have seen a surge of development for exploiting the relational information of input graphs. Nevertheless, messages propagating through a graph contain both interpretable patterns and small perturbations. Despite global noise could be distributed over the entire graph data, it is not uncommon that corruptions appear well-concealed and merely pollute local regions while still having a vital influence on the GNN learning and prediction performance. This work tackles the graph recovery problem from local poisons by a robustness representation learning. Our developed strategy identifies regional graph perturbations and formulates a robust hidden feature representation for GNNs. A mask function pinpointed the anomalies without prior knowledge, and an $\ell_{p,q}$ regularizer defends local poisonings through pursuing sparsity in the framelet domain while maintaining a conditional closeness between the observation and new representation. The proposed robust computational unit alleviates the inertial alternating direction method of multipliers to achieve an efficient solution. Extensive experiments show that our new model recovers graph representations from local pollution and achieves excellent performance.

Screening for Sparse Online Learning

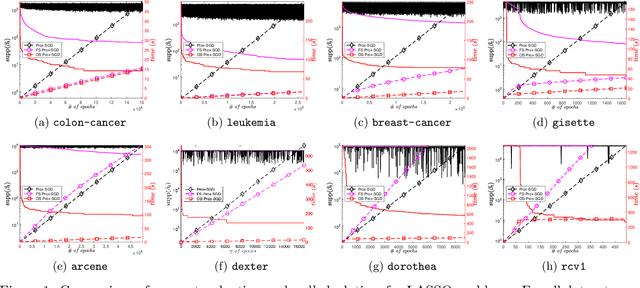
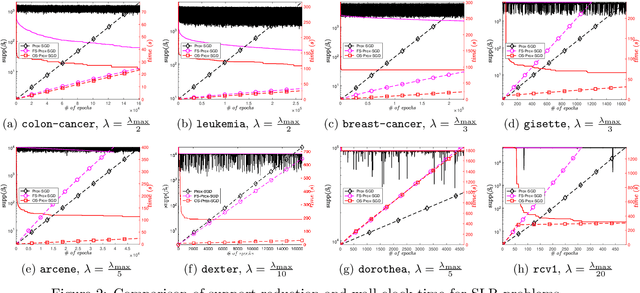
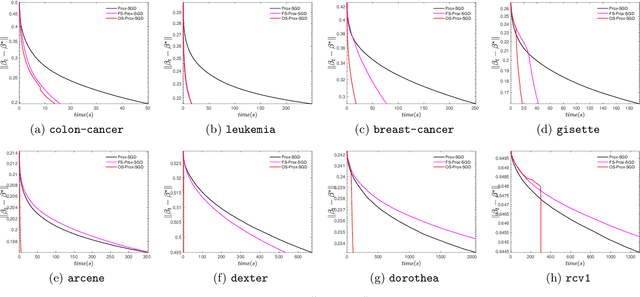
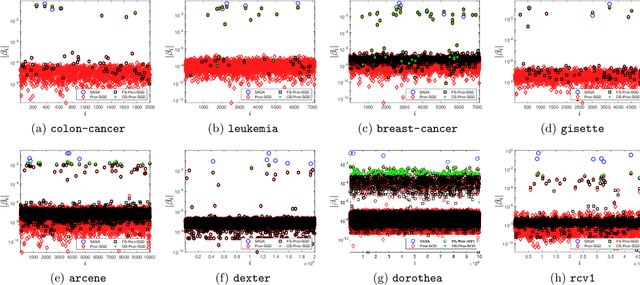
Sparsity promoting regularizers are widely used to impose low-complexity structure (e.g. l1-norm for sparsity) to the regression coefficients of supervised learning. In the realm of deterministic optimization, the sequence generated by iterative algorithms (such as proximal gradient descent) exhibit "finite activity identification", namely, they can identify the low-complexity structure in a finite number of iterations. However, most online algorithms (such as proximal stochastic gradient descent) do not have the property owing to the vanishing step-size and non-vanishing variance. In this paper, by combining with a screening rule, we show how to eliminate useless features of the iterates generated by online algorithms, and thereby enforce finite activity identification. One consequence is that when combined with any convergent online algorithm, sparsity properties imposed by the regularizer can be exploited for computational gains. Numerically, significant acceleration can be obtained.

TFPnP: Tuning-free Plug-and-Play Proximal Algorithm with Applications to Inverse Imaging Problems

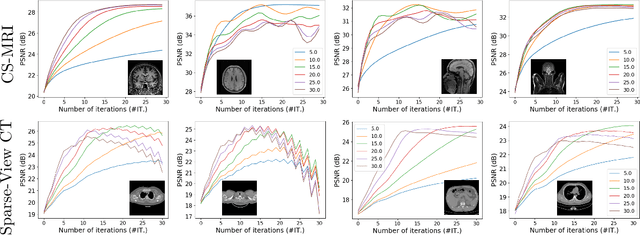
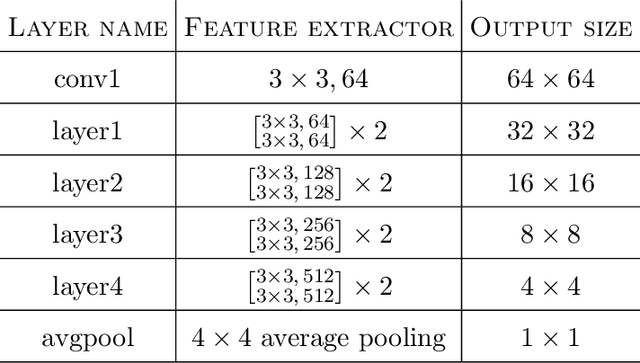
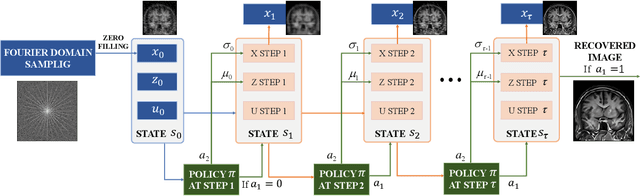
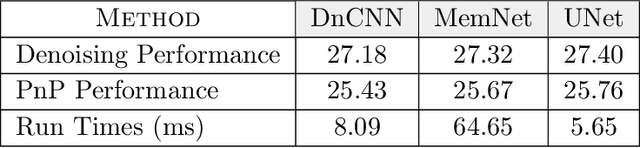
Plug-and-Play (PnP) is a non-convex framework that combines proximal algorithms, for example alternating direction method of multipliers (ADMM), with advanced denoiser priors. Over the past few years, great empirical success has been obtained by PnP algorithms, especially for the ones integrated with deep learning-based denoisers. However, a crucial issue of PnP approaches is the need of manual parameter tweaking. As it is essential to obtain high-quality results across the high discrepancy in terms of imaging conditions and varying scene content. In this work, we present a tuning-free PnP proximal algorithm, which can automatically determine the internal parameters including the penalty parameter, the denoising strength and the termination time. A core part of our approach is to develop a policy network for automatic search of parameters, which can be effectively learned via mixed model-free and model-based deep reinforcement learning. We demonstrate, through a set of numerical and visual experiments, that the learned policy can customize different parameters for different states, and often more efficient and effective than existing handcrafted criteria. Moreover, we discuss the practical considerations of the plugged denoisers, which together with our learned policy yield to state-of-the-art results. This is prevalent on both linear and nonlinear exemplary inverse imaging problems, and in particular, we show promising results on compressed sensing MRI, sparse-view CT and phase retrieval.

Tuning-free Plug-and-Play Proximal Algorithm for Inverse Imaging Problems

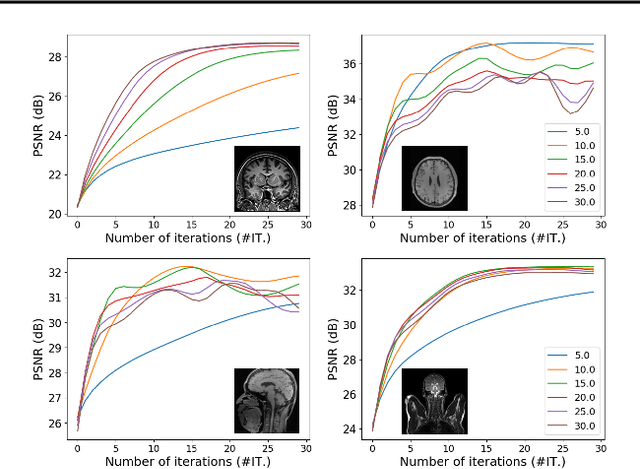
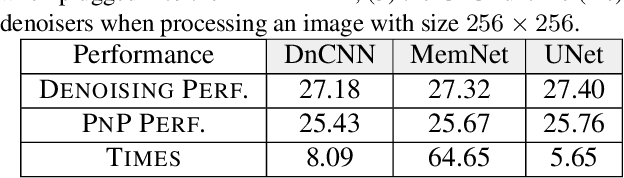
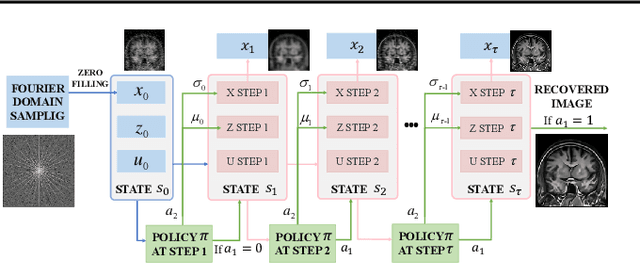
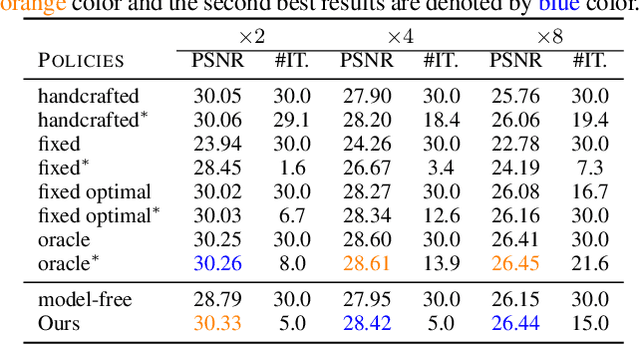
Plug-and-play (PnP) is a non-convex framework that combines ADMM or other proximal algorithms with advanced denoiser priors. Recently, PnP has achieved great empirical success, especially with the integration of deep learning-based denoisers. However, a key problem of PnP based approaches is that they require manual parameter tweaking. It is necessary to obtain high-quality results across the high discrepancy in terms of imaging conditions and varying scene content. In this work, we present a tuning-free PnP proximal algorithm, which can automatically determine the internal parameters including the penalty parameter, the denoising strength and the terminal time. A key part of our approach is to develop a policy network for automatic search of parameters, which can be effectively learned via mixed model-free and model-based deep reinforcement learning. We demonstrate, through numerical and visual experiments, that the learned policy can customize different parameters for different states, and often more efficient and effective than existing handcrafted criteria. Moreover, we discuss the practical considerations of the plugged denoisers, which together with our learned policy yield state-of-the-art results. This is prevalent on both linear and nonlinear exemplary inverse imaging problems, and in particular, we show promising results on Compressed Sensing MRI and phase retrieval.

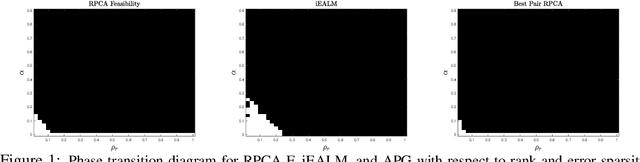
Best Pair Formulation & Accelerated Scheme for Non-convex Principal Component Pursuit

The best pair problem aims to find a pair of points that minimize the distance between two disjoint sets. In this paper, we formulate the classical robust principal component analysis (RPCA) as the best pair; which was not considered before. We design an accelerated proximal gradient scheme to solve it, for which we show global convergence, as well as the local linear rate. Our extensive numerical experiments on both real and synthetic data suggest that the algorithm outperforms relevant baseline algorithms in the literature.