Best Pair Formulation & Accelerated Scheme for Non-convex Principal Component Pursuit
Paper and Code
May 28, 2019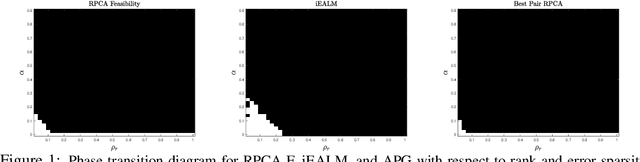


The best pair problem aims to find a pair of points that minimize the distance between two disjoint sets. In this paper, we formulate the classical robust principal component analysis (RPCA) as the best pair; which was not considered before. We design an accelerated proximal gradient scheme to solve it, for which we show global convergence, as well as the local linear rate. Our extensive numerical experiments on both real and synthetic data suggest that the algorithm outperforms relevant baseline algorithms in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge