Plug-and-Play Half-Quadratic Splitting for Ptychography

Ptychography is a coherent diffraction imaging method that uses phase retrieval techniques to reconstruct complex-valued images. It achieves this by sequentially illuminating overlapping regions of a sample with a coherent beam and recording the diffraction pattern. Although this addresses traditional imaging system challenges, it is computationally intensive and highly sensitive to noise, especially with reduced illumination overlap. Data-driven regularisation techniques have been applied in phase retrieval to improve reconstruction quality. In particular, plug-and-play (PnP) offers flexibility by integrating data-driven denoisers as implicit priors. In this work, we propose a half-quadratic splitting framework for using PnP and other data-driven priors for ptychography. We evaluate our method both on natural images and real test objects to validate its effectiveness for ptychographic image reconstruction.

Why do we regularise in every iteration for imaging inverse problems?

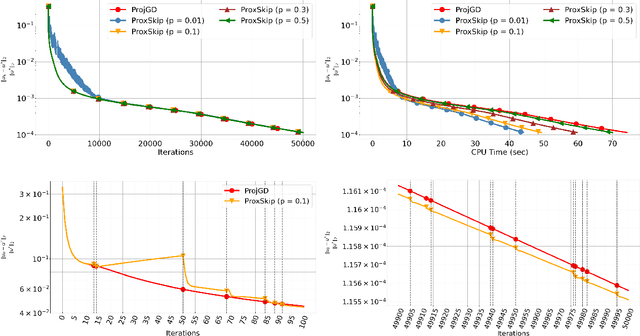
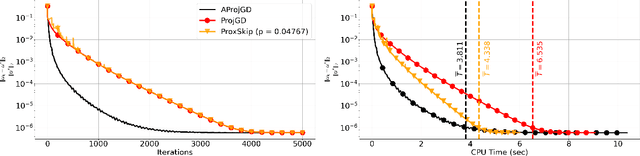
Regularisation is commonly used in iterative methods for solving imaging inverse problems. Many algorithms involve the evaluation of the proximal operator of the regularisation term in every iteration, leading to a significant computational overhead since such evaluation can be costly. In this context, the ProxSkip algorithm, recently proposed for federated learning purposes, emerges as an solution. It randomly skips regularisation steps, reducing the computational time of an iterative algorithm without affecting its convergence. Here we explore for the first time the efficacy of ProxSkip to a variety of imaging inverse problems and we also propose a novel PDHGSkip version. Extensive numerical results highlight the potential of these methods to accelerate computations while maintaining high-quality reconstructions.

Stochastic Optimisation Framework using the Core Imaging Library and Synergistic Image Reconstruction Framework for PET Reconstruction

We introduce a stochastic framework into the open--source Core Imaging Library (CIL) which enables easy development of stochastic algorithms. Five such algorithms from the literature are developed, Stochastic Gradient Descent, Stochastic Average Gradient (-Am\'elior\'e), (Loopless) Stochastic Variance Reduced Gradient. We showcase the functionality of the framework with a comparative study against a deterministic algorithm on a simulated 2D PET dataset, with the use of the open-source Synergistic Image Reconstruction Framework. We observe that stochastic optimisation methods can converge in fewer passes of the data than a standard deterministic algorithm.

A Guide to Stochastic Optimisation for Large-Scale Inverse Problems

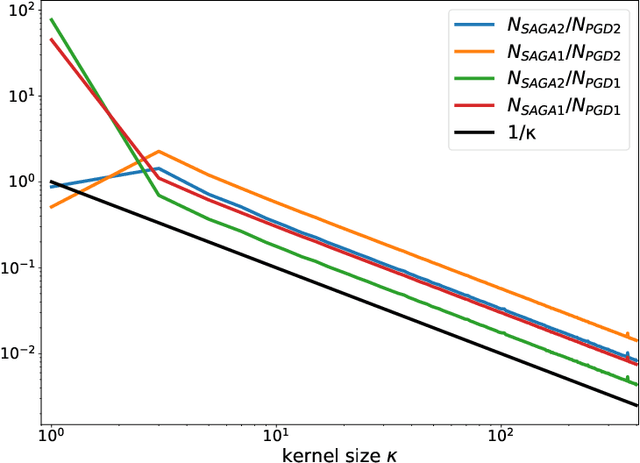
Stochastic optimisation algorithms are the de facto standard for machine learning with large amounts of data. Handling only a subset of available data in each optimisation step dramatically reduces the per-iteration computational costs, while still ensuring significant progress towards the solution. Driven by the need to solve large-scale optimisation problems as efficiently as possible, the last decade has witnessed an explosion of research in this area. Leveraging the parallels between machine learning and inverse problems has allowed harnessing the power of this research wave for solving inverse problems. In this survey, we provide a comprehensive account of the state-of-the-art in stochastic optimisation from the viewpoint of inverse problems. We present algorithms with diverse modalities of problem randomisation and discuss the roles of variance reduction, acceleration, higher-order methods, and other algorithmic modifications, and compare theoretical results with practical behaviour. We focus on the potential and the challenges for stochastic optimisation that are unique to inverse imaging problems and are not commonly encountered in machine learning. We conclude the survey with illustrative examples from imaging problems to examine the advantages and disadvantages that this new generation of algorithms bring to the field of inverse problems.

StreaMRAK a Streaming Multi-Resolution Adaptive Kernel Algorithm

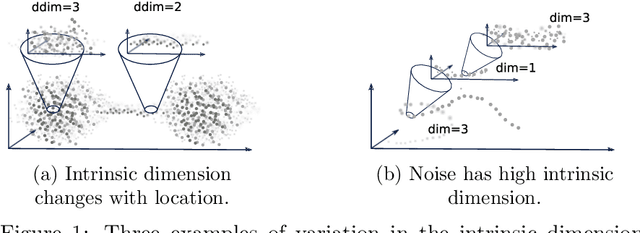
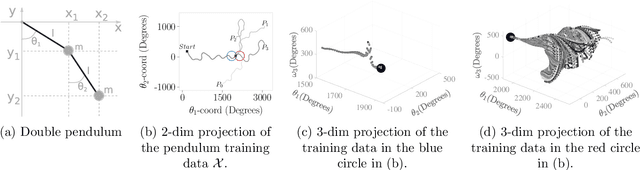
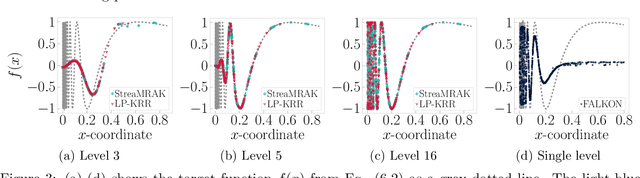
Kernel ridge regression (KRR) is a popular scheme for non-linear non-parametric learning. However, existing implementations of KRR require that all the data is stored in the main memory, which severely limits the use of KRR in contexts where data size far exceeds the memory size. Such applications are increasingly common in data mining, bioinformatics, and control. A powerful paradigm for computing on data sets that are too large for memory is the streaming model of computation, where we process one data sample at a time, discarding each sample before moving on to the next one. In this paper, we propose StreaMRAK - a streaming version of KRR. StreaMRAK improves on existing KRR schemes by dividing the problem into several levels of resolution, which allows continual refinement to the predictions. The algorithm reduces the memory requirement by continuously and efficiently integrating new samples into the training model. With a novel sub-sampling scheme, StreaMRAK reduces memory and computational complexities by creating a sketch of the original data, where the sub-sampling density is adapted to the bandwidth of the kernel and the local dimensionality of the data. We present a showcase study on two synthetic problems and the prediction of the trajectory of a double pendulum. The results show that the proposed algorithm is fast and accurate.

Unsupervised Knowledge-Transfer for Learned Image Reconstruction

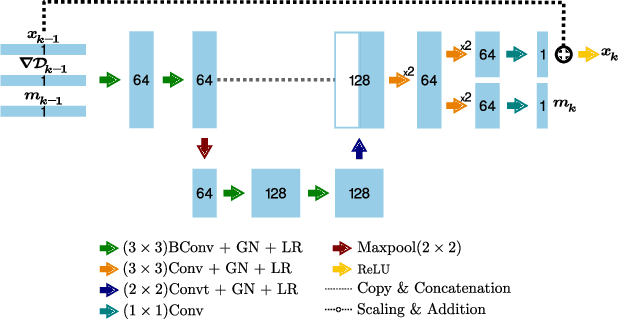
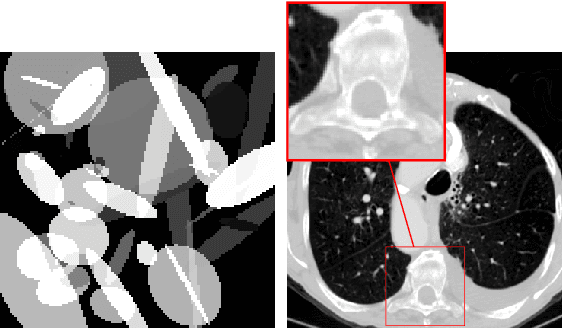
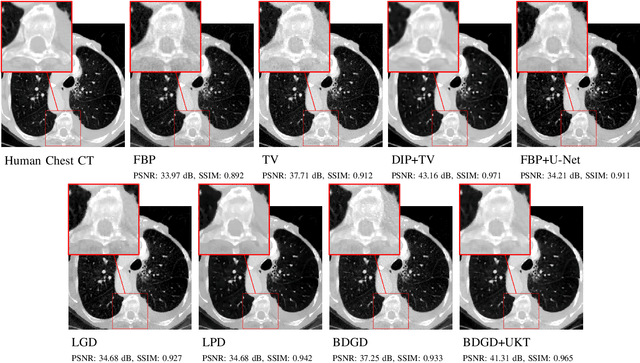
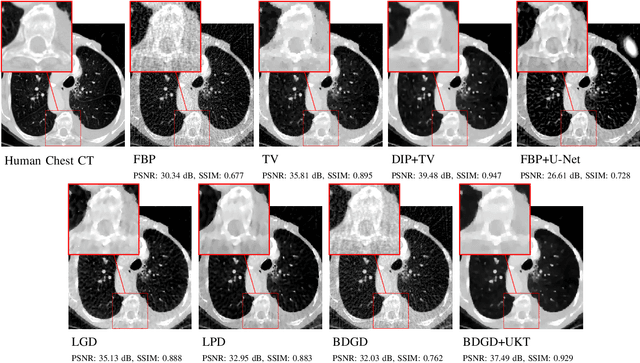
Deep learning-based image reconstruction approaches have demonstrated impressive empirical performance in many imaging modalities. These approaches generally require a large amount of high-quality training data, which is often not available. To circumvent this issue, we develop a novel unsupervised knowledge-transfer paradigm for learned iterative reconstruction within a Bayesian framework. The proposed approach learns an iterative reconstruction network in two phases. The first phase trains a reconstruction network with a set of ordered pairs comprising of ground truth images and measurement data. The second phase fine-tunes the pretrained network to the measurement data without supervision. Furthermore, the framework delivers uncertainty information over the reconstructed image. We present extensive experimental results on low-dose and sparse-view computed tomography, showing that the proposed framework significantly improves reconstruction quality not only visually, but also quantitatively in terms of PSNR and SSIM, and is competitive with several state-of-the-art supervised and unsupervised reconstruction techniques.

Estimating covariance and precision matrices along subspaces

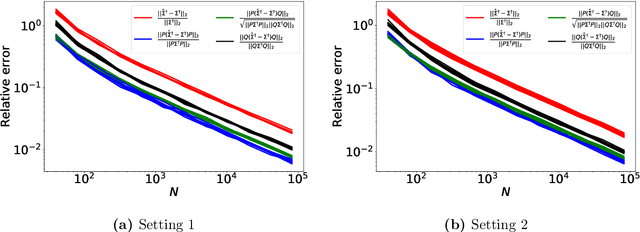
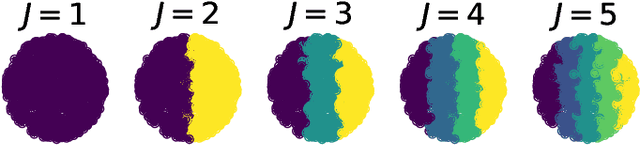
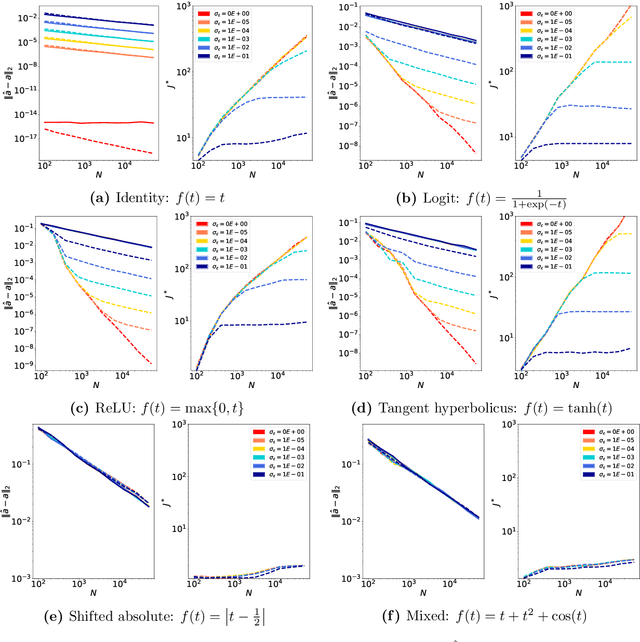
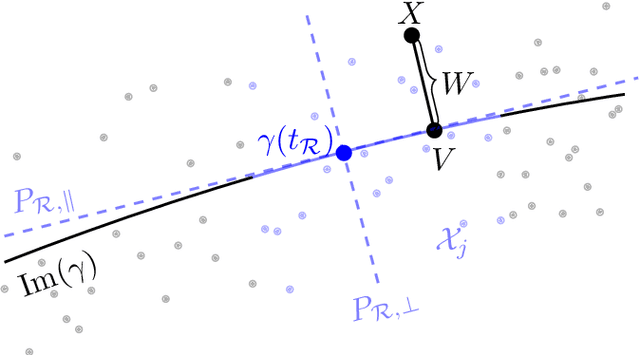
We study the accuracy of estimating the covariance and the precision matrix of a $D$-variate sub-Gaussian distribution along a prescribed subspace or direction using the finite sample covariance with $N \geq D$ samples. Our results show that the estimation accuracy depends almost exclusively only on the components of the distribution that correspond to desired subspaces or directions. This is relevant for problems where behavior of data along a lower-dimensional space is of specific interest, such as dimension reduction or structured regression problems. As a by-product of the analysis, we reduce the effect the matrix condition number has on the estimation of precision matrices. Two applications are presented: direction-sensitive eigenspace perturbation bounds, and estimation of the single-index model. For the latter, a new estimator, derived from the analysis, with strong theoretical guarantees and superior numerical performance is proposed.

Nonlinear generalization of the single index model

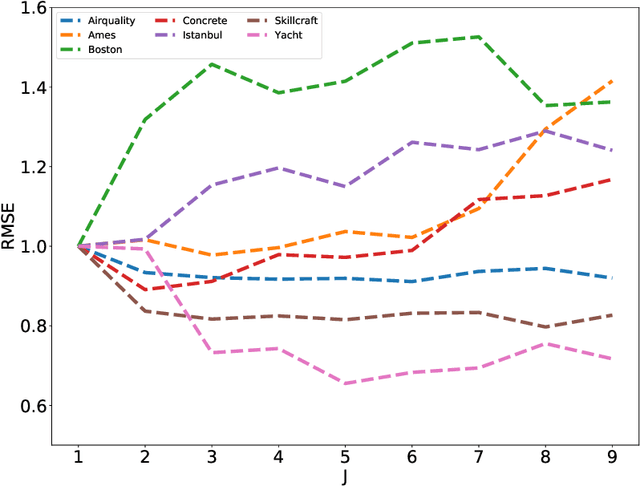
Single index model is a powerful yet simple model, widely used in statistics, machine learning, and other scientific fields. It models the regression function as $g(<a,x>)$, where a is an unknown index vector and x are the features. This paper deals with a nonlinear generalization of this framework to allow for a regressor that uses multiple index vectors, adapting to local changes in the responses. To do so we exploit the conditional distribution over function-driven partitions, and use linear regression to locally estimate index vectors. We then regress by applying a kNN type estimator that uses a localized proxy of the geodesic metric. We present theoretical guarantees for estimation of local index vectors and out-of-sample prediction, and demonstrate the performance of our method with experiments on synthetic and real-world data sets, comparing it with state-of-the-art methods.

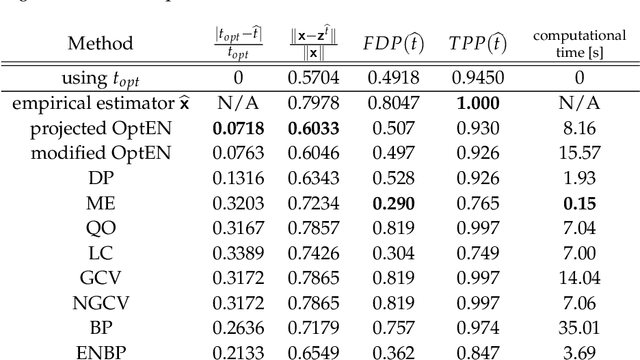
A Learning Theory Approach to a Computationally Efficient Parameter Selection for the Elastic Net

Despite recent advances in regularisation theory, the issue of parameter selection still remains a challenge for most applications. In a recent work the framework of statistical learning was used to approximate the optimal Tikhonov regularisation parameter from noisy data. In this work, we improve their results and extend the analysis to the elastic net regularisation, providing explicit error bounds on the accuracy of the approximated parameter and the corresponding regularisation solution in a simplified case. Furthermore, in the general case we design a data-driven, automated algorithm for the computation of an approximate regularisation parameter. Our analysis combines statistical learning theory with insights from regularisation theory. We compare our approach with state-of-the-art parameter selection criteria and illustrate its superiority in terms of accuracy and computational time on simulated and real data sets.