Nonlinear generalization of the single index model

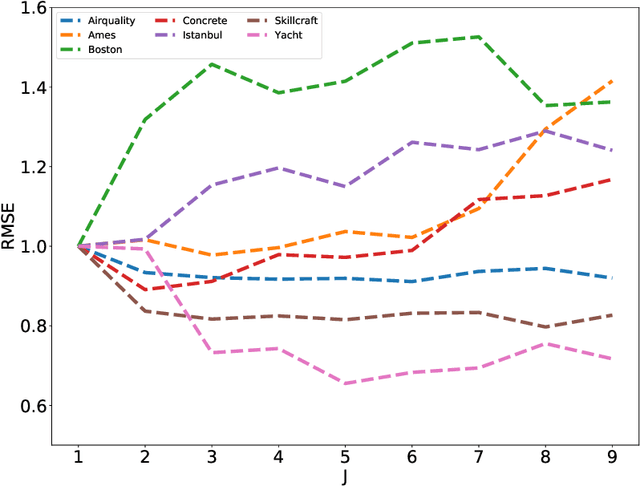
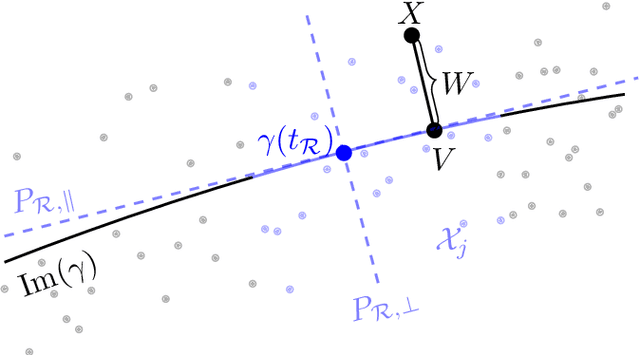
Single index model is a powerful yet simple model, widely used in statistics, machine learning, and other scientific fields. It models the regression function as $g(<a,x>)$, where a is an unknown index vector and x are the features. This paper deals with a nonlinear generalization of this framework to allow for a regressor that uses multiple index vectors, adapting to local changes in the responses. To do so we exploit the conditional distribution over function-driven partitions, and use linear regression to locally estimate index vectors. We then regress by applying a kNN type estimator that uses a localized proxy of the geodesic metric. We present theoretical guarantees for estimation of local index vectors and out-of-sample prediction, and demonstrate the performance of our method with experiments on synthetic and real-world data sets, comparing it with state-of-the-art methods.