G-Adaptive mesh refinement -- leveraging graph neural networks and differentiable finite element solvers

We present a novel, and effective, approach to the long-standing problem of mesh adaptivity in finite element methods (FEM). FE solvers are powerful tools for solving partial differential equations (PDEs), but their cost and accuracy are critically dependent on the choice of mesh points. To keep computational costs low, mesh relocation (r-adaptivity) seeks to optimise the position of a fixed number of mesh points to obtain the best FE solution accuracy. Classical approaches to this problem require the solution of a separate nonlinear "meshing" PDE to find the mesh point locations. This incurs significant cost at remeshing and relies on certain a-priori assumptions and guiding heuristics for optimal mesh point location. Recent machine learning approaches to r-adaptivity have mainly focused on the construction of fast surrogates for such classical methods. Our new approach combines a graph neural network (GNN) powered architecture, with training based on direct minimisation of the FE solution error with respect to the mesh point locations. The GNN employs graph neural diffusion (GRAND), closely aligning the mesh solution space to that of classical meshing methodologies, thus replacing heuristics with a learnable strategy, and providing a strong inductive bias. This allows for rapid and robust training and results in an extremely efficient and effective GNN approach to online r-adaptivity. This method outperforms classical and prior ML approaches to r-adaptive meshing on the test problems we consider, in particular achieving lower FE solution error, whilst retaining the significant speed-up over classical methods observed in prior ML work.

A fast neural hybrid Newton solver adapted to implicit methods for nonlinear dynamics

The use of implicit time-stepping schemes for the numerical approximation of solutions to stiff nonlinear time-evolution equations brings well-known advantages including, typically, better stability behaviour and corresponding support of larger time steps, and better structure preservation properties. However, this comes at the price of having to solve a nonlinear equation at every time step of the numerical scheme. In this work, we propose a novel operator learning based hybrid Newton's method to accelerate this solution of the nonlinear time step system for stiff time-evolution nonlinear equations. We propose a targeted learning strategy which facilitates robust unsupervised learning in an offline phase and provides a highly efficient initialisation for the Newton iteration leading to consistent acceleration of Newton's method. A quantifiable rate of improvement in Newton's method achieved by improved initialisation is provided and we analyse the upper bound of the generalisation error of our unsupervised learning strategy. These theoretical results are supported by extensive numerical results, demonstrating the efficiency of our proposed neural hybrid solver both in one- and two-dimensional cases.

Learning the Sampling Pattern for MRI

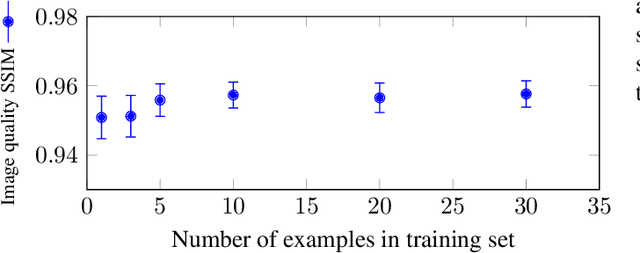
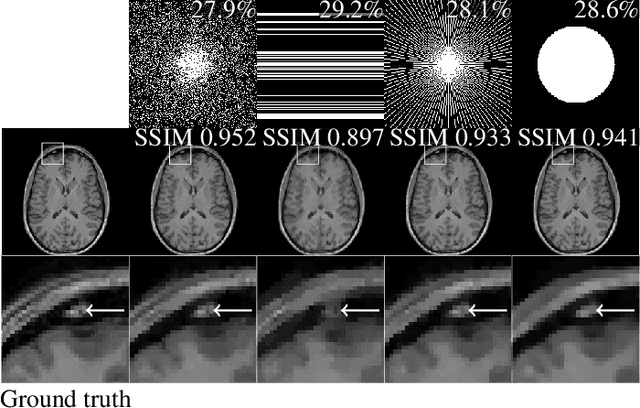
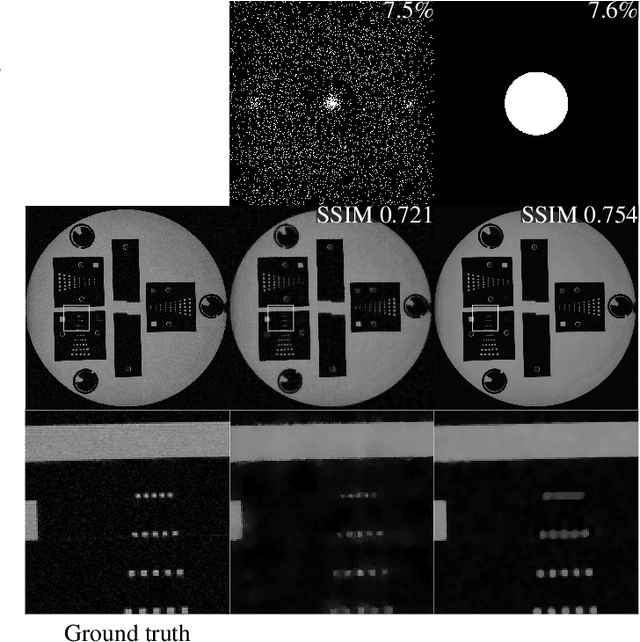
The discovery of the theory of compressed sensing brought the realisation that many inverse problems can be solved even when measurements are "incomplete". This is particularly interesting in magnetic resonance imaging (MRI), where long acquisition times can limit its use. In this work, we consider the problem of learning a sparse sampling pattern that can be used to optimally balance acquisition time versus quality of the reconstructed image. We use a supervised learning approach, making the assumption that our training data is representative enough of new data acquisitions. We demonstrate that this is indeed the case, even if the training data consists of just 5 training pairs of measurements and ground-truth images; with a training set of brain images of size 192 by 192, for instance, one of the learned patterns samples only 32% of k-space, however results in reconstructions with mean SSIM 0.956 on a test set of similar images. The proposed framework is general enough to learn arbitrary sampling patterns, including common patterns such as Cartesian, spiral and radial sampling.

Mirror, Mirror, on the Wall, Who's Got the Clearest Image of Them All? - A Tailored Approach to Single Image Reflection Removal

Removing reflection artefacts from a single-image is a problem of both theoretical and practical interest. Removing these artefacts still presents challenges because of the massively ill-posed nature of reflection suppression. In this work, we propose a technique based on a novel optimisation problem. Firstly, we introduce an $H^2$ fidelity term, which preserves fine detail while enforcing global colour similarity. Secondly, we introduce a spatially dependent gradient sparsity prior, which allows user guidance to prevent information loss in reflection-free areas. We show that this combination allows us to mitigate some major drawbacks of the existing methods for reflection removal. We demonstrate, through numerical and visual experiments, that our method is able to outperform the state-of-the-art methods and compete against a recent deep learning approach.

Peekaboo - Where are the Objects? Structure Adjusting Superpixels

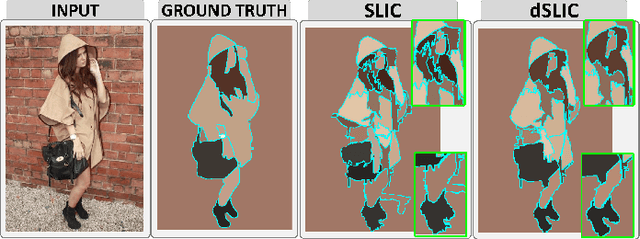
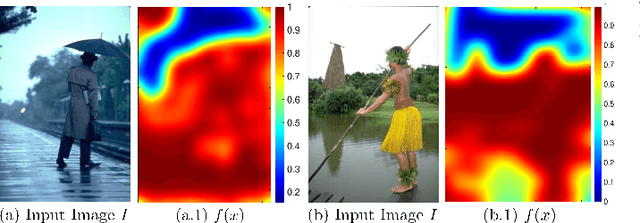
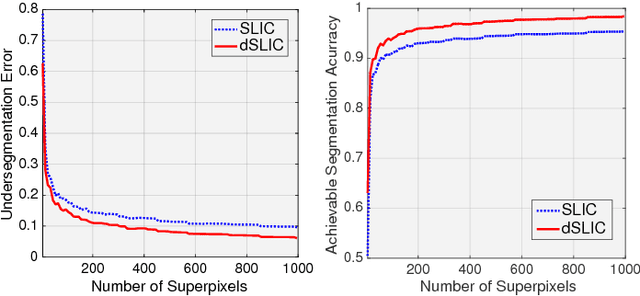
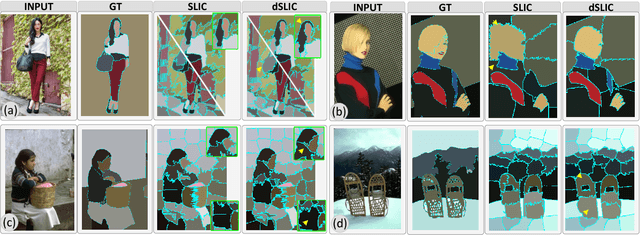
This paper addresses the search for a fast and meaningful image segmentation in the context of $k$-means clustering. The proposed method builds on a widely-used local version of Lloyd's algorithm, called Simple Linear Iterative Clustering (SLIC). We propose an algorithm which extends SLIC to dynamically adjust the local search, adopting superpixel resolution dynamically to structure existent in the image, and thus provides for more meaningful superpixels in the same linear runtime as standard SLIC. The proposed method is evaluated against state-of-the-art techniques and improved boundary adherence and undersegmentation error are observed, whilst still remaining among the fastest algorithms which are tested.