Delving Into Deep Walkers: A Convergence Analysis of Random-Walk-Based Vertex Embeddings

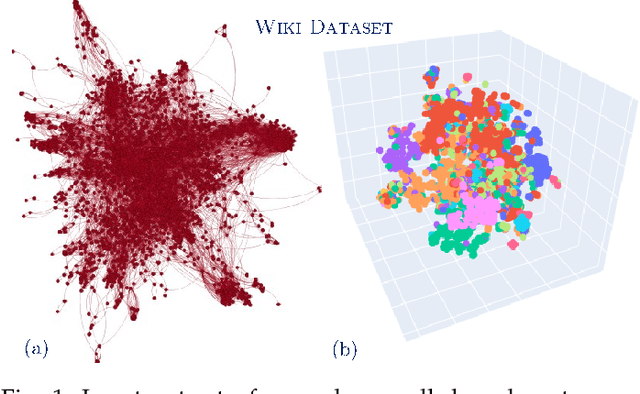
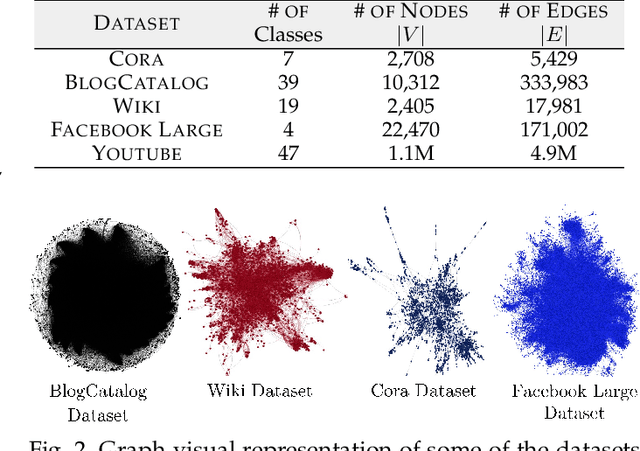
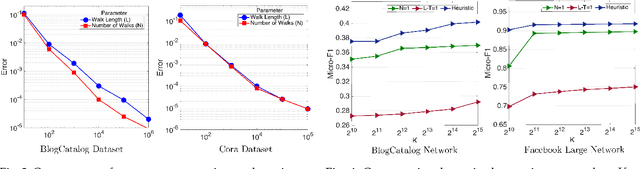
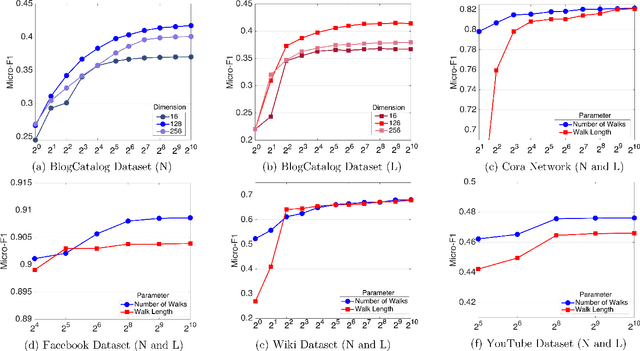
Graph vertex embeddings based on random walks have become increasingly influential in recent years, showing good performance in several tasks as they efficiently transform a graph into a more computationally digestible format while preserving relevant information. However, the theoretical properties of such algorithms, in particular the influence of hyperparameters and of the graph structure on their convergence behaviour, have so far not been well-understood. In this work, we provide a theoretical analysis for random-walks based embeddings techniques. Firstly, we prove that, under some weak assumptions, vertex embeddings derived from random walks do indeed converge both in the single limit of the number of random walks $N \to \infty$ and in the double limit of both $N$ and the length of each random walk $L\to\infty$. Secondly, we derive concentration bounds quantifying the converge rate of the corpora for the single and double limits. Thirdly, we use these results to derive a heuristic for choosing the hyperparameters $N$ and $L$. We validate and illustrate the practical importance of our findings with a range of numerical and visual experiments on several graphs drawn from real-world applications.

Dynamic Spectral Residual Superpixels

We consider the problem of segmenting an image into superpixels in the context of $k$-means clustering, in which we wish to decompose an image into local, homogeneous regions corresponding to the underlying objects. Our novel approach builds upon the widely used Simple Linear Iterative Clustering (SLIC), and incorporate a measure of objects' structure based on the spectral residual of an image. Based on this combination, we propose a modified initialisation scheme and search metric, which helps keeps fine-details. This combination leads to better adherence to object boundaries, while preventing unnecessary segmentation of large, uniform areas, while remaining computationally tractable in comparison to other methods. We demonstrate through numerical and visual experiments that our approach outperforms the state-of-the-art techniques.

Mirror, Mirror, on the Wall, Who's Got the Clearest Image of Them All? - A Tailored Approach to Single Image Reflection Removal

Removing reflection artefacts from a single-image is a problem of both theoretical and practical interest. Removing these artefacts still presents challenges because of the massively ill-posed nature of reflection suppression. In this work, we propose a technique based on a novel optimisation problem. Firstly, we introduce an $H^2$ fidelity term, which preserves fine detail while enforcing global colour similarity. Secondly, we introduce a spatially dependent gradient sparsity prior, which allows user guidance to prevent information loss in reflection-free areas. We show that this combination allows us to mitigate some major drawbacks of the existing methods for reflection removal. We demonstrate, through numerical and visual experiments, that our method is able to outperform the state-of-the-art methods and compete against a recent deep learning approach.

Peekaboo - Where are the Objects? Structure Adjusting Superpixels

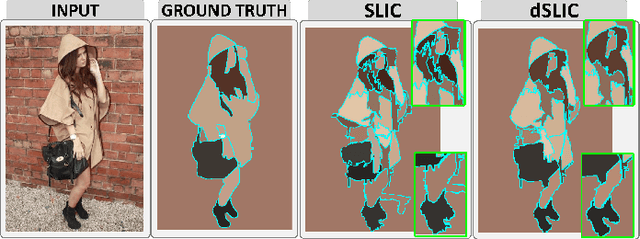
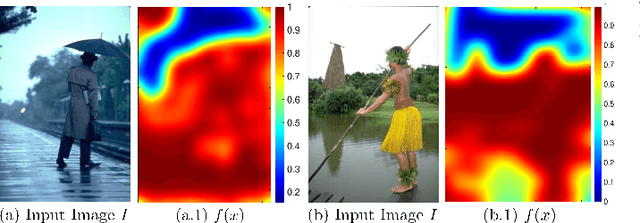
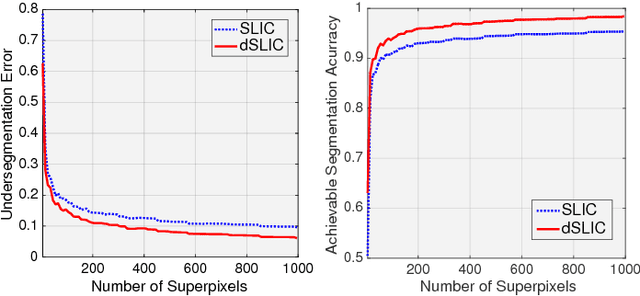
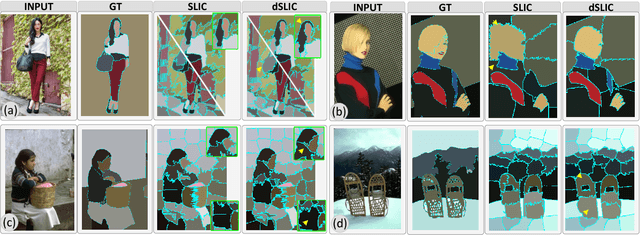
This paper addresses the search for a fast and meaningful image segmentation in the context of $k$-means clustering. The proposed method builds on a widely-used local version of Lloyd's algorithm, called Simple Linear Iterative Clustering (SLIC). We propose an algorithm which extends SLIC to dynamically adjust the local search, adopting superpixel resolution dynamically to structure existent in the image, and thus provides for more meaningful superpixels in the same linear runtime as standard SLIC. The proposed method is evaluated against state-of-the-art techniques and improved boundary adherence and undersegmentation error are observed, whilst still remaining among the fastest algorithms which are tested.